Having defined optional and predictable projections in an earlier post, I now look at their basic properties. The first nontrivial property is that they are well-defined in the first place. Recall that existence of the projections made use of the existence of cadlag modifications of martingales, and uniqueness relied on the section theorems. By contrast, once we accept that optional and predictable projections are well-defined, everything in this post follows easily. Nothing here requires any further advanced results of stochastic process theory.
Optional and predictable projections are similar in nature to conditional expectations. Given a probability space and a sub-sigma-algebra
, the conditional expectation of an (
-measurable) random variable X is a
-measurable random variable
. This is defined whenever the integrability condition
(a.s.) is satisfied, only depends on X up to almost-sure equivalence, and Y is defined up to almost-sure equivalence. That is, a random variable
almost surely equal to X has the same conditional expectation as X. Similarly, a random variable
almost-surely equal to Y is also a version of the conditional expectation
.
The setup with projections of stochastic processes is similar. We start with a filtered probability space , and a (real-valued) stochastic process is a map
which we assume to be jointly-measurable. That is, it is measurable with respect to the Borel sigma-algebra on the image, and the product sigma-algebra
on the domain. The optional and predictable sigma-algebras are contained in the product,
We do not have a reference measure on in order to define conditional expectations with respect to
and
. However, the optional projection
and predictable projection
play similar roles. Assuming that the necessary integrability properties are satisfied, then the projections exist. Furthermore, the projection only depends on the process X up to evanescence (i.e., up to a zero probability set), and
and
are uniquely defined up to evanescence.
In what follows, we work with respect to a complete filtered probability space. Processes are always only considered up to evanescence, so statements involving equalities, inequalities, and limits of processes are only required to hold outside of a zero probability set. When we say that the optional projection of a process exists, we mean that the integrability condition in the definition of the projection is satisfied. Specifically, that is almost surely finite. Similarly for the predictable projection.
The following lemma gives a list of initial properties of the optional projection. Other than the statement involving stopping times, they all correspond to properties of conditional expectations.
Lemma 1
- X is optional if and only if
exists and is equal to X.
- If the optional projection of X exists then,
(1) - If the optional projections of X and Y exist, and
are
-measurable random variables, then,
(2) - If the optional projection of X exists and U is an optional process then,
(3) - If the optional projection of X exists and
is a stopping time then, the optional projection of the stopped process
exists and,
(4) - If
and the optional projections of X and Y exist then,
.
Before proceeding with the proof of the lemma, I briefly note that, throughout this post, stochastic processes will be assumed to take the value 0 at time . This merely saves a bit of writing, as we can write
in place of
.
Proof: For the first statement, is optional by definition, so X is optional if
. Conversely, if X is optional then
is
-measurable for each stopping time
. So,
is finite, and the optional projection of X exists. Similarly,
, so the optional projection of X is equal to itself.
For the second statement, is optional, so (1) follows from the first statement with
in place of X.
Moving on to the third statement, linearity of conditional expectations gives
which is finite, if the optional projections of X and Y exist. So, the optional projection of exists. Similarly,
As is optional, this shows that it is the optional projection of
.
For the fourth statement, as U is optional, is
-measurable. So,
is almost surely finite, and the optional projection of exists.
As is optional, this shows that it is the optional projection of
.
For the fifth statement, consider a stopping time . As the optional projection of X exists,
is almost surely finite. So, is almost surely finite, and the optional projection of
exists. As
is left-continuous and adapted, it is predictable and, in particular, is optional. Applying (3)
By optional section, this proves (4).
For the final statement, if then, by monotonicity of conditional expectations,
almost surely. By optional section, . ⬜
Unsurprisingly, the list of properties above also apply to predictable projections.
Lemma 2
- X is predictable if and only if
exists and is equal to X.
- If the predictable projection of X exists then,
- If the predictable projections of X and Y exist, and
are
-measurable random variables, then,
- If the predictable projection of X exists and U is a predictable process then,
- If the predictable projection of X exists and
is a stopping time then, the predictable projection of
exists and,
- If
and the predictable projections of X and Y exist then,
.
Proof: Each statement follows in exactly the same way as for Lemma 1, replacing `optional’ by `predictable’ and sigma algebras by
. ⬜
Next, for sigma-algebras , the tower rule for conditional expectations states that
Similarly for the projections of a stochastic process, we have the following.
Lemma 3 If the predictable and optional projections of X exist then,
Proof: As is predictable, it is optional, so the equality
is immediate. For a predictable stopping time
As the predictable projection exists, this is almost surely finite. So, the predictable projection of exists and,
So, . ⬜
As with expectations and conditional expectations, the projections satisfy dominated convergence.
Lemma 4 (Dominated Convergence) Let
be a sequence of processes such that
as n goes to infinity, and Y be a process with
for all n.
- If the optional projection of Y exists, then
.
- If the predictable projection of Y exists, then
.
Proof: It is standard that the set on which a sequence of random variables converges to a given limit is measurable. Specifically, a sequence converges to a limit X whenever, for each
there exists positive m such that
for all
. It is enough to consider
so that,
Applying this to the optional projections, is optional. For any stopping time
, applying dominated convergence to the conditional expectations,
almost surely. So whenever
(a.s.). This means that
and
are optional projections of
and X respectively. Hence, by uniqueness of optional projections,
up to evanescence.
The same argument applies to predictable projections, replacing `optional’ by `predictable’, `stopping time’ by `predictable stopping time’, and by
. ⬜
We now look at special cases where the projections can be described explicitly. We use to denote the left-limits of a process
.
Lemma 5 Suppose that X is the constant process
, for some integrable random variable U. Then, the optional and predictable projections of X exist and,
Here, M is the martingale defined by
. In the case where the underlying filtration is right-continuous, we choose the cadlag version of M. More generally, if a cadlag version does not exist, we can take M to be the version with left and right limits everywhere, and right-continuous outside a countable subset of
.
Proof: This is just a restatement of lemma 7 of the post on the projection theorems, where it was used to prove the existence of optional and predictable projections. ⬜
The predictable projection of a local martingale is given by its left limits.
Lemma 6 If M is a local martingale then its predictable projection exists and,
Proof: We proved this previously in the post on constructing martingales with prescribed jumps. However, the result was established there by an application of a much stronger statement. As the result is really quite elementary, I will give a more direct proof here.
First, as is left-continuous and adapted, it is predictable and, so,
. Next, as M is locally integrable, the conditional expectation
is almost-surely finite for each predictable stopping time
. So, the predictable projections of M and
exist.
Suppose now that M is a proper martingale, is a bounded predictable stopping time, and
are stopping times announcing
. For any
and
,
| (5) |
The first equality uses the fact that is uniformly integrable and, the second equality is an application of optional sampling, which applies for
(so that
) and, hence, holds for the limit
. As (5) holds for all A in
, which generates
as a sigma-algebra, the monotone class theorem implies that (5) holds for all
. By definition, this means that
almost surely.
If M is a local martingale, let be a localizing sequence of stopping times, so that
are proper martingales. Then, using dominated convergence for the conditional expectations, for a bounded predictable stopping time
,
Hence, . Finally,
⬜
Optional projections of progressively measurable processes are particularly simple, and always exist, without requiring any integrability conditions.
Lemma 7 If X is progressive then its optional projection exists and is the unique optional process satisfying
whenever
(almost surely) for every stopping time
.
Proof: For any stopping time ,
is measurable w.r.t.
. Then,
is finite. So, from the definition, the optional projection exists and is the unique process satisfying
almost surely, for all stopping times . ⬜
Thin Processes
Recall that a subset of is thin if it is equal to the union of the graphs of a countable sequence of stopping times, and that a process X is thin if it is optional and
is a thin set. For example, for a cadlag adapted process, its jump process
is thin. Lemma 6 above looked at one special case of the predictable projection of a thin process, specifically that the jumps of a local martingale has predictable projection equal to zero.
For the theory of optional and predictable processes, we are concerned with processes which are not necessarily adapted to the underlying filtration. So, we generalise the concept a bit. A subset S of will be called a raw thin set if it is the union of the graphs of a sequence of
-measurable times
,
| (6) |
A raw thin process X will refer to any jointly measurable process such that is a raw thin set. We note that, in the definition of raw thin sets, it is enough for (6) to hold with the inequality
in place of equality, and for S to be jointly measurable. In that case, we can replace the random times
by
defined such that
whenever
and equal to
elsewhere. These will be measurable, so long as S is jointly measurable, and we recover equality in (6).
In the current situation, the relevant property is that optional and predictable projection preserves thinness.
Theorem 8 The optional and predictable projections of a raw thin process are thin, whenever they exist.
I do not prove this immediately. Instead, in a moment, we will give constructions of the projection of a raw thin process, which will demonstrate that it is thin. For now, we note the following corollary.
Corollary 9 If the optional and predictable projections of X exists then
is thin.
Proof: As is optional, it can be expressed as a sum
of a predictable process Y and a thin process H. Then, the predictable process Y has predictable projection equal to itself. Using the identity
,
Theorem 8 says that this is thin. ⬜
The first step in showing that the optional projection of a raw thin process X is thin is to find a sequence of stopping times such that
for all stopping times
. It would then follow that
is contained in
and that
is thin. For the predictable projection, we need to do the same thing but with `predictable stopping time’ replacing `stopping time’. Consider a collection
of measurable times
. We will say that a jointly measurable subset S of
is inaccessible by
if
for all
. The following simple result will be applied in the cases where
is the collection of all stopping times, and when it is the collection of all predictable stopping times.
Lemma 10 Let
be a raw thin set and
be any collection of measurable times
. Then, there exists a sequence
such that
is inaccessible by
.
Proof: As S is equal to for a sequence
of random times, we can define a finite measure
on
by
Define
This supremum can be attained as follows. Choose sequences with
approaching
as m goes to infinity. It follows that
. Rearranging the doubly indexed sequence
into a singly indexed one,
, we can write
. Then,
is in
and,
Writing , it remains to be shown that
is inaccessible by
. So, consider any
. By construction, we have
and, hence,
for all n. Therefore,
as required. ⬜
We now compute the optional projection of a raw thin process. Note that the existence of the sequence, , of stopping times, is guaranteed by lemma 10.
Lemma 11 Let X be a raw thin process and
be a sequence of stopping times such that
is inaccessible by stopping times.
The optional projection of X exists if and only if
is almost surely finite for each n. In that case,
is the unique process with
.
almost surely, for each n.
Proof: First, from the definition, the condition that is almost surely finite is necessary for the optional projection to exist. We show that it is also sufficient. Consider any stopping time
. Using the fact that
is in both
and
, and that the sigma-algebras agree on this set,
almost surely. Also, letting , the condition that
is inaccessible by stopping times gives
almost surely. In any case, this shows that is almost surely finite, so the optional projection of X exists.
Now, for any stopping time then, as shown above for
,
so, by optional section, or, equivalently,
. The final property stated for
is immediate from the definition of the optional projection.
Finally, it is clear that the two statements of the lemma uniquely determine (up to evanescence). The first statement defines
outside of S and the second defines it on S. ⬜
Next, we can compute the predictable projection of a raw thin process in a similar fashion as for the optional projection in lemma 11. Again, the existence of the sequence, , of predictable stopping times, is guaranteed by lemma 10.
Lemma 12 Let X be a raw thin process and
be a sequence of predictable stopping times such that
is inaccessible by predictable stopping times.
The predictable projection of X exists if and only if
is almost surely finite for each n. In that case,
is the unique process with
.
almost surely, for each n.
Proof: This follows using the same argument as for lemma 11, replacing `optional’ by `predictable’, `stopping time’ by `predictable stopping time’, and sigma-algebras by
. ⬜
Finally, theorem 8 is an immediate consequence of lemmas 11 and 12.
Dear George
In the proof of lemma 6, when you treat the case of local martingales, on the second to last string of equalities you say that in order to prove it you use dominated convergence for conditional expectations, can you please explain what exactly mean by that ?
If we have convergence of random variables and dominated as
and dominated as  where
where ![\mathbb E[Y\vert\mathcal G] < \infty](https://s0.wp.com/latex.php?latex=%5Cmathbb+E%5BY%5Cvert%5Cmathcal+G%5D+%3C+%5Cinfty&bg=ffffff&fg=000000&s=0&c=20201002) (a.s.) then
(a.s.) then ![\mathbb E[X^n\vert\mathcal G]\to\mathbb E[X\vert\mathcal G]](https://s0.wp.com/latex.php?latex=%5Cmathbb+E%5BX%5En%5Cvert%5Cmathcal+G%5D%5Cto%5Cmathbb+E%5BX%5Cvert%5Cmathcal+G%5D&bg=ffffff&fg=000000&s=0&c=20201002) (a.s.).
(a.s.).
Dear George,
Well yes, but who is the dominator of the sequence ?
?
It is dominated by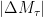 which has finite conditional expectation as local martingales are locally integrable https://almostsuremath.com/2009/12/23/localization/#scn_local_lem11
which has finite conditional expectation as local martingales are locally integrable https://almostsuremath.com/2009/12/23/localization/#scn_local_lem11