On The Integral ∫I(W ≥ 0)dW

In this post I look at the integral X_t = ∫₀^t 1_{W≥0} dW for standard Brownian motion W. This is a particularly interesting example of stochastic integration with connections to local times, option pricing and hedging, and demonstrates behaviour not seen for deterministic integrals that can seem counter-intuitive. For a start, X is a martingale so has zero expectation. To some it might, at first, seem that X is nonnegative and — furthermore — equals W ∨ 0. However, this has positive expectation contradicting the first property. In fact, X can go negative and we can compute its distribution. In a Twitter post, Oswin So asked about this very point, showing some plots demonstrating the behaviour of the integral.

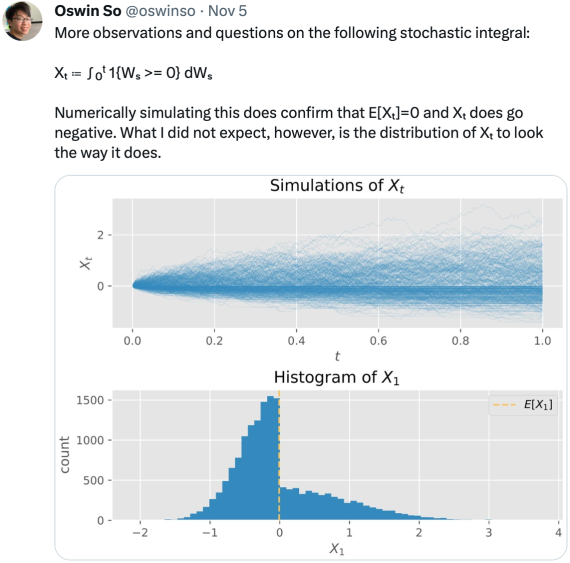
We can evaluate the integral as X_t = W_t ∨ 0 – 12 L_t⁰ where L_t⁰ is the local time of W at 0. The local time is a continuous increasing process starting from 0, and only increases at times where W = 0. That is, it is constant over intervals on which W is nonzero. The first term, W_t ∨ 0 has probability density p(x) equal to that of a normal density over x > 0 and has a delta function at zero. Subtracting the nonnegative value L⁰_t spreads out the density of this delta function to the left, leading to the odd looking density computed numerically in So’s Twitter post, with a peak just to the left of the origin and dropping instantly to a smaller value on the right. We will compute an exact form for this probability density but, first, let’s look at an intuitive interpretation in the language of option pricing.

Consider a financial asset such as a stock, whose spot price at time t is S_t. We suppose that the price is defined at all times t ≥ 0 and has continuous sample paths. Furthermore, suppose that we can buy and sell at spot any time with no transaction costs. A call option of strike price K and maturity T pays out the cash value (S_T - K)₊ at time T. For simplicity, assume that this is ‘out of the money’ at the initial time, meaning that S₀ ≤ K.

The idea of option hedging is, starting with an initial investment, to trade in the stock in such a way that at maturity T, the value of our trading portfolio is equal to (S_T - K)₊. This synthetically replicates the option. A naive suggestion which is sometimes considered is to hold one unit of stock at all times t for which S_t ≥ K and zero units at all other times.The profit from such a strategy is given by the integral X_T = ∫₀^T 1_{S≥K} dS. If the stock only equals the strike price at finitely many times then this works. If it first hits K at time s and does not drop back below it on interval (s, t) then the profit at t is equal to the amount S_t – K that it has gone up since we purchased it. If it drops back below the strike then we sell at K for zero profit or loss, and this repeats for subsequent times that it exceeds K. So, at time T, we hold one unit of stock if its value is above K for a profit of S_T – K and zero units for zero profit otherwise. This replicates the option payoff.

The idea described works if S_T hits the strike K at a finite set of times,and also if the path of S_t has finite variation, in which case Lebesgue-Stieltjes integration gives X_T = (S_T - K)₊. It cannot work for stock prices though! If it did, then we have a trading strategy which is guaranteed to never lose money but generates profits on the positive probability event that S_T > K. This is arbitrage, generating money with zero risk, which should be impossible.

What goes wrong? First, Brownian motion does not have sample paths with finite variation and will not hit a level finitely often. Instead, if it reaches K then it hits the level uncountably often. As our simple trading strategy would involve buying and selling infinitely often, it is not so easy. Instead, we can approximate by a discrete-time strategy and take the limit. Choosing a finite sequence of times 0 = t₀ < t₁ < ⋯< t_n = T, the discrete approximation is to hold one unit of the asset over the interval (t_i, t_i+1] if S_ti ≥ K and zero units otherwise.

The discrete strategy involves buying one unit of the asset whenever its price reaches K at one of the discrete times and selling whenever it drops back below. This replicates the option payoff, except for the fact then when we buy above K we effectively overpay by amount S_ti – K and, when we sell below K, we lose K – S_ti. This results in some slippage from not being able to execute at the exact level,

So, our simple trading strategy generates profit (S_T - K)₊ – A_T, missing the option value by amount A_T. In the limit as n goes to infinity with time step size going to zero, the slippage A_T does not go to zero. For equally spaced times, It can be shown that the number of times that spot crosses K is of order √n, and each of these times generates slippage of order 1/√n on average. So, in the limit, A_T does not vanish and, instead, converges on a positive value equal to half the local time L_T^K.

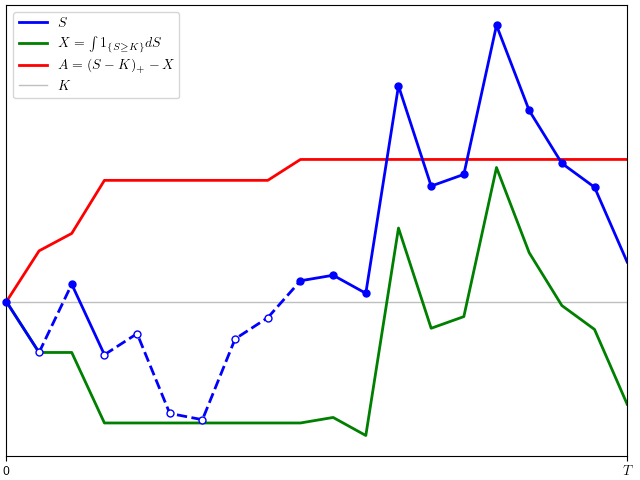
Figure 2 shows the situation, with the slippage A shown on the same plot (using K as the zero axis, so they are on the same scale). We can just take K = 0 for an asset whose spot price can be positive or negative. Then, with S = W, our integral X_T = ∫₀^T 1_{W≥0} dW is the same as the payoff from the naive option hedge, or (S_T)₊ minus slippage L⁰_T/2.

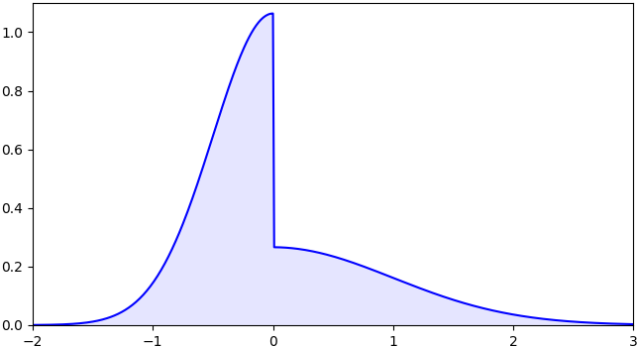
Now lets turn to a computation of the probability density of X_T = W_T ∨ 0 – L_T⁰/2. By the scaling property of Brownian motion, the distribution of X_T/√T does not depend on T, so we take T = 1 without loss of generality. The first trick to this is to make use of the fact that, if M_t = sup_s≤tW_s is the running maximum then (|W_t|, L_t⁰) has the same joint distribution as (M_t - W_t, M_t). This immediately tells us that L₁⁰ has the same distribution as M₁ which, by the reflection principle, has the same distribution as |W₁|. Using

for the standard normal density, this shows that the local time L₁⁰ has probability density 2φ(x) over x > 0.

Next, as flipping the sign W does not impact either |W₁| or L₁⁰, sgn(W₁) is independent of these. On the event W₁ < 0 we have X₁ = –L₁⁰/2 which has density 4φ(2x) over x < 0. On the event W₁ > 0, we have X₁ = |W₁|-L₁⁰/2, which has the same distribution as M₁/2 – W₁.

To complete the computation of the probability density of X₁, we need to know the joint distribution of M₁ and W₁, which can be done as described in the post on the reflection principle. The probability that W₁ is in an interval of width δx about a point x and that M₁ > y, for some y > x is, by reflection, equal to the probability that W₁ is in an interval of width δx about the point 2y – x. This has probability φ(2y - x)δx and, by differentiating in y, gives a joint probability density of 2φ′(x - 2y) for (W₁, M₁).

The expectation of f(X₁) for bounded measurable function f can be computed by integrating over this joint probability density.

The substitution z = y/2 – x was applied in the inner integral, and the order of integration switched. The probability density of X₁ conditioned on W₁ > 0 is therefore,

Conditioned on W₁ < 0, we have already shown that the density is 4φ(2x) over x < 0 so, taking the average of these, we obtain

This is plotted in figure 3 below, agreeing with So’s numerical estimation from the Twitter post shown in figure 1 above.