Algebraic Probability

The aim of this post is to motivate the idea of representing probability spaces as states on a commutative algebra. We will consider how this abstract construction relates directly to classical probabilities.

In the standard axiomatization of probability theory, due to Kolmogorov, the central construct is a probability space ${(\Omega,\mathcal F,{\mathbb P})}$ . This consists of a state space ${\Omega}$ , an event space ${\mathcal F}$ , which is a sigma-algebra of subsets of ${\Omega}$ , and a probability measure ${{\mathbb P}}$ . The measure ${{\mathbb P}}$ is defined as a map ${{\mathbb P}\colon\mathcal F\rightarrow{\mathbb R}^+}$ satisfying countable additivity and normalised as ${{\mathbb P}(\Omega)=1}$ .

A measure space allows us to define integrals of real-valued measurable functions or, in the language of probability, expectations of random variables. We construct the set ${L^\infty(\Omega,\mathcal F)}$ of all bounded measurable functions ${X\colon\Omega\rightarrow{\mathbb R}}$ . This is a real vector space and, as it is closed under multiplication, is an algebra. Expectation, by definition, is the unique linear map ${L^\infty\rightarrow{\mathbb R}}$ , ${X\mapsto{\mathbb E}[X]}$ satisfying ${{\mathbb E}[1_A]={\mathbb P}(A)}$ for ${A\in\mathcal F}$ and monotone convergence: if ${X_n\in L^\infty}$ is a nonnegative sequence increasing to a bounded limit ${X}$ , then ${{\mathbb E}[X_n]}$ tends to ${{\mathbb E}[X]}$ .

In the opposite direction, any nonnegative linear map ${p\colon L^\infty(\Omega,\mathcal F)\rightarrow{\mathbb R}}$ satisfying monotone convergence and ${p(1)=1}$ defines a probability measure by ${{\mathbb P}(A)=p(1_A)}$ . This is the unique measure with respect to which expectation agrees with the linear map, ${{\mathbb E}=p}$ . So, probability measures are in one-to-one correspondence with such linear maps, and they can be viewed as one and the same thing. The Kolmogorov definition of a probability space can be thought of as representing the expectation on the subset of ${L^\infty}$ consisting of indicator functions ${1_A}$ . In practice, it is often more convenient to start with a different subset of ${L^\infty}$ . For example, probability measures on ${{\mathbb R}^+}$ can be defined via their Laplace transform, ${\mathcal L_{{\mathbb P}}(a)=\int e^{-ax}d{\mathbb P}(x)}$ , which represents the expectation on exponential functions ${x\mapsto e^{-ax}}$ . Generalising to complex-valued random variables, probability measures on ${{\mathbb R}}$ are often represented by their characteristic function ${\varphi(a)=\int e^{iax}d{\mathbb P}(x)}$ , which is just the expectation of the complex exponentials ${x\mapsto e^{iax}}$ . In fact, by the monotone class theorem, we can uniquely represent probability measures on ${(\Omega,\mathcal F)}$ by the expectations on any subset ${\mathcal K\subseteq L^\infty}$ which is closed under taking products and generates the sigma-algebra ${\mathcal F}$ .

A simple corollary of the monotone class theorem states that there is a one-to-one correspondence between sigma-algebras on a set ${\Omega}$ and algebras ${\mathcal A}$ of bounded functions ${\Omega\rightarrow{\mathbb R}}$ closed under monotone convergence, with the correspondence given by ${\mathcal A=L^\infty(\Omega,\mathcal F)}$ .

On the other hand, in quantum mechanics, we start with a Hilbert space ${\mathcal H}$ , and observables are represented as self-adjoint operators. Restricting our consideration to bounded observables, these generate a subalgebra of ${B(\mathcal H)}$ , the space of bounded linear maps on ${\mathcal H}$ . A pure state is represented by an element ${\psi\in\mathcal H}$ normalised so that ${\langle\psi,\psi\rangle=1}$ , and the expectation of an observable ${X}$ is ${\langle X\rangle=\langle\psi,X\psi\rangle}$ . This is a nonnegative linear map from a sub-algebra of ${B(\mathcal H)}$ to ${{\mathbb C}}$ .

All of this suggests that it would be useful to consider an alternative approach to probability. Instead of a measurable space ${(\Omega,\mathcal F)}$ , we have an algebra ${\mathcal A}$ . Instead of a probability measure ${{\mathbb P}}$ , we have a positive linear map ${p}$ from ${\mathcal A}$ to ${{\mathbb R}}$ or ${{\mathbb C}}$ . The underlying state space ${\Omega}$ is not required at all — it is a pointless approach to probability, as we no longer include the points ${\omega\in\Omega}$ in the representation of the probability space. As multiplication of real (and complex) numbers is commutative, ${xy=yx}$ , algebras of the form ${L^\infty(\Omega,\mathcal F)}$ are commutative. Hence, classical probability spaces will correspond to commutative algebras, with the generalisation to non-commutative algebras incorporating quantum probability.

As this post is primarily intended to motivate the algebraic approach to probability, rather than go into technical details, I will not give proofs of all theorems quoted here and, instead, will refer to the literature. We start with the definition of an algebra.

Definition 1 Let ${K}$ be a field. Then, a ${K}$ -algebra, or algebra over ${K}$ , is a ${K}$ -vector space ${\mathcal A}$ equipped with a binary product, ${(a,b)\mapsto ab}$ , and identity element ${I\in\mathcal A}$ satisfying the following for all ${a,b,c\in\mathcal A}$ .

Associativity: ${a(bc)=(ab)c}$ .

Compatability with scalars: ${\lambda(ab)=(\lambda a)b=a(\lambda b)}$ for all ${\lambda\in K}$ .

Left-distributivity: ${a(b+c)=ab+ac}$ .

Right-distributivity: ${(a+b)c=ac+bc}$

Identity: ${Ia=aI=a}$ .

If, furthermore, ${ab=ba}$ for all ${a,b\in\mathcal A}$ then the algebra is said to be commutative.

Strictly speaking, this defines a unitial associative algebra. Sometimes, the axiom of associativity is dropped, although I do not look at such non-associative algebras here. Similarly, the existence of the identity ${I}$ is sometimes dropped along with its corresponding axiom. In this post, whenever the unqualified term `algebra’ is used, then it refers to a structure ${\mathcal A}$ satisfying definition 1, so is unitial. Also, I will use the symbol ${1}$ to denote the identity element. This creates some ambiguity as to whether an expression of the form ${1a}$ refers to multiplication by the identity element ${1}$ or by the scalar ${1\in K}$ . However, as they both evaluate to ${a}$ , it should not cause any confusion.

A subset ${S\subseteq\mathcal A}$ is called commutative if ${ab=ba}$ for all ${a,b\in S}$ . In particular, the algebra itself is commutative if and only if ${\mathcal A}$ is commutative as a set of elements. It is also easy to show that the sub-algebra of ${\mathcal A}$ generated by a commutative set ${S}$ (i.e., the smallest subalgebra containing ${S}$ ) is itself commutative. Note that this means that the subalgebra generated by a single element is commutative.

Examples of algebras abound in mathematics. A small set of examples is:

Polynomial rings ${K[X_1,X_2,\ldots,X_n]}$ are commutative ${K}$ -algebras.
For a set ${E}$ , the collection of functions ${f\colon E\rightarrow K}$ is a commutative ${K}$ -algebra, where the operations of addition, scalar multiplication, and multiplication are defined point-wise.
For a measurable space ${(E,\mathcal E)}$ , the collection of ${\mathcal E}$ -measurable functions ${f\colon E\rightarrow{\mathbb R}}$ is an ${{\mathbb R}}$ -algebra.
For a normed real vector space ${V}$ , the collection of bounded linear maps ${V\rightarrow V}$ is an ${{\mathbb R}}$ -algebra.

We define the notion of a state on a commutative real algebra.

Definition 2 Let ${\mathcal A}$ be a commutative real algebra. Then, a linear map ${p\colon\mathcal A\rightarrow{\mathbb R}}$ is

positive if ${p(a^2)\ge0}$ for all ${a\in\mathcal A}$ .

a state if it is positive and ${p(1)=1}$ .

Correspondence with classical probabilities

As discussed above, a classical probability space determines a commutative real algebra, consisting of the bounded random variables, and a state on this algebra given by expectation. The question is, can this process be inverted? When can a state ${p}$ on a commutative real algebra ${\mathcal A}$ be represented as an expectation on a set of random variables on some probability space? We start by considering a single element ${a\in\mathcal A}$ . This defines a map ${{\mathbb R}[X]\rightarrow\mathcal A}$ taking any polynomial ${f}$ to its evaluation ${f(a)}$ , and the image is the sub-algebra generated by ${\mathcal A}$ . For ${a}$ to be considered as a random variable on a probability space, then its distribution ${\mu}$ is a probability measure on ${{\mathbb R}}$ satisfying

$\displaystyle p(f(a))=\int f(x)d\mu(x)$

(1)

for all polynomials ${f\in{\mathbb R}[X]}$ . By linearity, (1) holds whenever it holds on monomials ${f=X^n}$ . That is, we require

$\displaystyle \int x^nd\mu(x)=p(a^n)$

for all positive integers ${n}$ and, for this to make sense, ${\mu}$ must have finite moments. This is the classical moment problem, to construct a probability measure from its moments. In the one factor case, it is known that the positivity of ${p}$ ensures existence of a solution.

Theorem 3 Let ${p}$ be a state on commutative real algebra ${\mathcal A}$ . Then, for any ${a\in\mathcal A}$ , there exists a probability measure ${\mu}$ on ${{\mathbb R}}$ satisfying (1).

The existence of a measure with specified moments is known as the Hamburger problem. Unfortunately, uniqueness need not hold, as there do exist distinct probability measures on ${{\mathbb R}}$ with the same moments. As an example, consider the log-normal distribution on the nonnegative reals, and a perturbation of this,

$\displaystyle \setlength\arraycolsep{2pt} \begin{array}{rl} &\displaystyle d\mu(x)=\sqrt{2\pi}x^{-1}e^{-\frac12(\log x)^2}dx,\smallskip\\ &\displaystyle d\nu(x)=(1+\sin(2\pi\log x))d\mu(x). \end{array}$

These measures have all the same moments,

$\displaystyle \int x^nd\mu(x)=\int x^nd\nu(x)=e^{\frac12n^2},$

and therefore generate the same state on the algebra ${\mathcal A={\mathbb R}[X]}$ . On the other hand, it is not difficult to show that the distribution of a bounded random variable is uniquely determined by its moments. This follows from the Stone–Weierstrass theorem, which states that the polynomials are dense in the space of continuous functions on any closed bounded interval. Furthermore, the distribution ${\mu}$ will be supported by an interval ${[-K,K]}$ if ${p(a^{2n})^{\frac1{2n}}\le K}$ for all positive ${n}$ . It is possible to relax this condition to bounds on the growth of the moments, such as Carleman’s condition (2).

Theorem 4 Let ${p}$ be a state on commutative real algebra ${\mathcal A}$ . If ${a\in\mathcal A}$ satisfies

$\displaystyle \sum_{n=1}^\infty p(a^{2n})^{-\frac{1}{2n}}=\infty,$ (2)

then there exists a unique probability measure ${\mu}$ on ${{\mathbb R}}$ satisfying (1).

This result goes back to T. Carleman, Les fonctions quasi analytiques, Gauthier–Villars, Paris, 1926. A proof of this result, and also of the Hamburger problem, is given in the lecture notes, The classical moment problem, by Sasha Sodin, 2019. See Theorem 3.1 and Corollary 2.12.

Moving to the mutifactor situation, where we have a sequence ${a_1,a_2,\ldots,a_m\in\mathcal A}$ , the aim is to find a probability measure ${\mu}$ on ${{\mathbb R}^m}$ satisfying

$\displaystyle p(f(a_1,\ldots,a_m))=\int f(x_1,\ldots,x_m)d\mu(x_1,\ldots,x_m)$

(3)

for all polynomials ${f\in{\mathbb R}[X_1,\ldots,X_m]}$ and, as in the single factor case, ${\mu}$ must have finite moments for this to make sense. Unlike the single factor case, this is not always possible, so theorem 3 does not generalise to ${m > 1}$ . The reason for this is that there exists multifactor polynomials which are positive on all of ${{\mathbb R}^m}$ , yet cannot be expressed as a sum of squares. Consider

$\displaystyle f=1+X^4Y^2+X^2Y^4-3X^2Y^2\in{\mathbb R}[X,Y].$

The AM-GM inequality shows that ${f\ge0}$ everywhere on ${{\mathbb R}^2}$ . However, it is not possible to express ${f}$ as ${\sum_if_i^2}$ for a finite sequence of polynomials ${f_i\in{\mathbb R}[X,Y]}$ . This means that the definition of positivity for a state ${p}$ on ${{\mathbb R}[X,Y]}$ is insufficient to ensure that ${p(f)\ge0}$ , and the hyperplane separation theorem implies the existence of states with ${p(f) < 0}$ . No such state can arise from the expectation under a probability measure.

Fortunately, if sufficient bounds are imposed on the growth of the moments ${p(a_k^n)}$ , then it is possible to show that a unique measure ${\mu}$ exists satisfying (3). Again, in the case that ${\rho(a_k^{2n})^{\frac1{2n}}\le K}$ for all ${k,n}$ and some real ${K}$ , then the Stone–Weierstrass theorem can be used to show uniqueness of ${\mu}$ , which must be supported on ${[-K,K]^m}$ , with the Riesz representation theorem providing existence. These conditions can be weakened considerably and, in fact, it is known that Carleman’s condition for each of the individual elements ${a_k}$ is sufficient to guarantee existence and uniqueness.

Theorem 5 Let ${p}$ be a state on commutative real algebra ${\mathcal A}$ . If ${a_1,\ldots,a_m\in\mathcal A}$ each satisfy Carleman’s condition (2) then there is a unique probability measure ${\mu}$ on ${{\mathbb R}^m}$ satisfying (3).

This result originates from Nussbaum, A. E., Quasi-analytic vectors, Arkiv för Matematik. 6 (1965), no. 2, 179–191.

Taking the idea a step further, we can consider infinite subsets ${\{a_i\colon i\in I\}}$ of ${\mathcal A}$ . Let ${{\mathbb R}^I}$ be the space of functions ${\omega\colon I\rightarrow {\mathbb R}}$ and ${X_i\colon{\mathbb R}^I\rightarrow{\mathbb R}}$ denote the coordinate map ${X_i(\omega)=\omega(i)}$ . Let ${\mathcal F}$ be the sigma-algebra on ${{\mathbb R}^I}$ generated by ${\{X_i\colon i\in I\}}$ . That is, ${\mathcal F}$ is the smallest sigma-algebra on ${{\mathbb R}^I}$ with respect to which each ${X_i}$ is measurable. In particular, it is generated by the sets ${X_i^{-1}(S)}$ for Borel ${S\subseteq{\mathbb R}}$ . The collection ${\{X_i\}}$ generates an algebra ${\mathcal X}$ of random variables, which can be expressed as real polynomials in ${\{X_i\}}$ . Evaluating the polynomials at the values ${a_i}$ gives an algebra homomorphism ${\varphi\colon\mathcal X\rightarrow\mathcal A}$ . The aim is to find a probability measure ${{\mathbb P}}$ on ${R^I}$ satisfying

$\displaystyle {\mathbb E}[X]=p(\varphi(X))$

(4)

for all ${X\in\mathcal X}$ which, to make sense, requires ${X}$ to be integrable.

If we choose ${\{a_i\colon i\in I\}}$ to be a generating set for ${\mathcal A}$ , so that the smallest subalgebra of ${\mathcal A}$ containing every ${a_i}$ is all of ${\mathcal A}$ , then we obtain a representation of ${(\mathcal A,p)}$ as an algebra of random variables on a probability space together with the expectation operator.

Theorem 6 Let ${p}$ be a state on commutative real algebra ${\mathcal A}$ . If ${\{a_i\colon i\in I\}\subseteq\mathcal A}$ each satisfy Carleman’s condition (2) then, there exists a unique probability measure ${{\mathbb P}}$ on ${{\mathbb R}^I}$ satisfying (4).

Proof: For each finite subset ${J=\{j_1,\ldots,j_m\}\subseteq I}$ , theorem 5 uniquely determines a probability measure ${\mu_J}$ on ${{\mathbb R}^J}$ satisfying

$\displaystyle \int f(\omega(j_1),\ldots,\omega(j_m))d\mu_J(\omega)=p(f(a_{j_1},\ldots,a_{j_m}))$

for all polynomials ${f\in{\mathbb R}[X_1,\ldots,X_m]}$ .

Define the projection map ${\pi^J\colon R^I\rightarrow{\mathbb R}^J}$ by ${\pi^J(\omega)(j)=\omega(j)}$ for all ${\omega\in{\mathbb R}^I}$ and ${j\in J}$ . For a probability measure ${{\mathbb P}}$ on ${{\mathbb R}^I}$ , the pushforward measure ${\pi^J_*{\mathbb P}}$ on ${{\mathbb R}^J}$ is defined by ${\pi^J_*{\mathbb P}(S)={\mathbb P}((\pi^J)^{-1}(S))}$ . Condition (4) is then,

$\displaystyle \setlength\arraycolsep{2pt} \begin{array}{rl} \displaystyle p(f(a_{j_1},\ldots,a_{j_m}))&\displaystyle={\mathbb E}[f(X_{j_1},\ldots,X_{j_m})]\smallskip\\ &\displaystyle=\int f(\omega(j_1),\ldots,\omega(j_m))d{\mathbb P}(\omega)\smallskip\\ &\displaystyle=\int f(\omega(j_1),\ldots,\omega(j_m))d\pi^J_*{\mathbb P}(\omega) \end{array}$

or, equivalently, ${\pi^J_*{\mathbb P}=\mu_J}$ . Existence and uniqueness of ${{\mathbb P}}$ follows from Kolmogorov’s extension theorem. ⬜

Continued…

3 thoughts on “Algebraic Probability”

Alex says:

26 December 19 at 2:11 PM

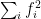This a great post, I can’t wait to read the continued notes. I have a question on the example $f=1+X^4Y^2+X^2Y^4-3X^2Y^2$ ,we can indeed prove that $f\ge 0$ using AM-GM inequality. But I didn’t not understand the sentence that $f$ cannot be expressed as $\sum_i f_i^2$ , do you mean that each 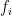$f_i$ is a polynomial in one variable, otherwise we can write $f=(\sqrt{f})^2$ . Also, can you develop a little bit how do you use the hyperplane separation theorem to prove the existence of states with $p(f)<0$ ? Thanks

1. George Lowther says:
  
  26 December 19 at 3:18 PM
  
  I mean that each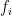 $f_i$ is in $\mathbb R[X,Y]$ [I edited]. I might come back and add some detail on the use of the hyperplane separation theorem, but it is intended as a brief counterexample and was wanting to get some new posts up first. Alternatively, should be able to find reference giving more detail on this.
  
  1. Alex says:
    
    26 December 19 at 4:58 PM
    
    Thank you for your quick reply. I can wait , atfer all I really want to learn the quantum part note.

	Harry on Filtrations and Adapted P…
	Anonymous on Analytic Sets
	Daniel on Analytic Sets
	Sid on Martingale Convergence
	northwiz on Preservation of the Local Mart…
	George Lowther on Martingale Convergence
	Sid on Martingale Convergence
	George Lowther on The Burkholder-Davis-Gundy Ine…
	George Lowther on Preservation of the Local Mart…
	northwiz on Preservation of the Local Mart…

Algebraic Probability

Correspondence with classical probabilities

Published by George Lowther

3 thoughts on “Algebraic Probability”

Leave a Reply to Alex Cancel reply

Correspondence with classical probabilities

Like this:

Related

Published by George Lowther

3 thoughts on “Algebraic Probability”

Leave a Reply to Alex Cancel reply