Martingales and Elementary Integrals

A martingale is a stochastic process which stays the same, on average. That is, the expected future value conditional on the present is equal to the current value. Examples include the wealth of a gambler as a function of time, assuming that he is playing a fair game. The canonical example of a continuous time martingale is Brownian motion and, in discrete time, a symmetric random walk is a martingale. As always, we work with respect to a filtered probability space ${(\Omega,\mathcal{F},\{\mathcal{F}_t\}_{t\ge 0},{\mathbb P})}$ . A process ${X}$ is said to be integrable if the random variables ${X_t}$ are integrable, so that ${{\mathbb E}[\vert X_t\vert]<\infty}$ .

Definition 1 A martingale, ${X}$ , is an integrable process satisfying

$\displaystyle X_s={\mathbb E}[X_t\mid\mathcal{F}_s]$

for all ${s<t\in{\mathbb R}_+}$ .

Continue reading “Martingales and Elementary Integrals” →

Predictable Stopping Times

The concept of a stopping times was introduced a couple of posts back. Roughly speaking, these are times for which it is possible to observe when they occur. Often, however, it is useful to distinguish between different types of stopping times. A random time for which it is possible to predict when it is about to occur is called a predictable stopping time. As always, we work with respect to a filtered probability space 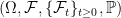${(\Omega,\mathcal{F},\{\mathcal{F}_t\}_{t\ge 0},{\mathbb P})}$ .

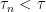Definition 1 A map ${\tau\colon\Omega\rightarrow\bar{\mathbb R}_+}$ is a predictable stopping time if there exists a sequence of stopping times ${\tau_n\uparrow\tau}$ satisfying ${\tau_n<\tau}$ whenever ${\tau\not=0}$ .

Predictable stopping times are alternatively referred to as previsible. The sequence of times ${\tau_n}$ in this definition are said to announce ${\tau}$ . Note that, in this definition, the random time was not explicitly required to be a stopping time. However, this is automatically the case, as the following equation shows.

$\displaystyle \left\{\tau\le t\right\}=\bigcap_n\left\{\tau_n\le t\right\}\in\mathcal{F}_t.$

One way in which predictable stopping times occur is as hitting times of a continuous adapted process. It is easy to predict when such a process is about to hit any level, because it must continuously approach that value.

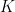Theorem 2 Let ${X}$ be a continuous adapted process and ${K}$ be a real number. Then

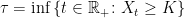
$\displaystyle \tau=\inf\left\{t\in{\mathbb R}_+\colon X_t\ge K\right\}$

is a predictable stopping time.

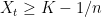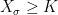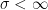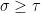Proof: Let ${\tau_n}$ be the first time at which ${X_t\ge K-1/n}$ which, by the debut theorem, is a stopping time. This gives an increasing sequence bounded above by ${\tau}$ . Also, ${X_{\tau_n}\ge K-1/n}$ whenever ${\tau_n<\infty}$ and, by left-continuity, setting ${\sigma=\lim_n\tau_n}$ gives ${X_\sigma\ge K}$ whenever ${\sigma<\infty}$ . So, ${\sigma\ge\tau}$ , showing that the sequence ${\tau_n}$ increases to ${\tau}$ . If ${0<\tau_n\le\tau<\infty}$ then, by continuity, 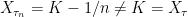${X_{\tau_n}=K-1/n\not=K=X_{\tau}}$ . 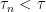So, ${\tau_n<\tau}$ whenever 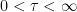${0<\tau<\infty}$ and the sequence 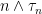${n\wedge\tau_n}$ announces ${\tau}$ . ⬜

In fact, predictable stopping times are always hitting times of continuous processes, as stated by the following result. Furthermore, by the second condition below, it is enough to prove the much weaker condition that a random time can be announced `in probability’ to conclude that it is a predictable stopping time.

Lemma 3 Suppose that the filtration is complete and ${\tau\colon\Omega\rightarrow\bar{\mathbb R}_+}$ is a random time. The following are equivalent.

${\tau}$ is a predictable stopping time.

For any ${\epsilon,\delta,K>0}$ there is a stopping time ${\sigma}$ satisfying

$\displaystyle {\mathbb P}\left(K\wedge\tau-\epsilon<\sigma<\tau{\rm\ or\ }\sigma=\tau=0\right)>1-\delta.$ (1)

${\tau=\inf\{t\ge 0\colon X_t=0\}}$ for some continuous adapted process ${X}$ .

Continue reading “Predictable Stopping Times” →

Sigma Algebras at a Stopping Time

The previous post introduced the notion of a stopping time ${\tau}$ . A stochastic process ${X}$ can be sampled at such random times and, if the process is jointly measurable, ${X_\tau}$ will be a measurable random variable. It is usual to study adapted processes, where ${X_t}$ is measurable with respect to the sigma-algebra ${\mathcal{F}_t}$ at that time. Then, it is natural to extend the notion of adapted processes to random times and ask the following. What is the sigma-algebra of observable events at the random time ${\tau}$ , and is ${X_\tau}$ measurable with respect to this? The idea is that if a set ${A}$ is observable at time ${\tau}$ then for any time ${t}$ , its restriction to the set ${\{\tau\le t\}}$ should be in ${\mathcal{F}_t}$ . As always, we work with respect to a filtered probability space ${(\Omega,\mathcal{F},\{\mathcal{F}_t\}_{t\ge 0},{\mathbb P})}$ . The sigma-algebra at the stopping time ${\tau}$ is then,

$\displaystyle \mathcal{F}_\tau=\left\{A\in\mathcal{F}_\infty\colon A\cap\{\tau\le t\}\in\mathcal{F}_t{\rm\ for\ all\ }t\ge 0\right\}.$

The restriction to sets in ${\mathcal{F}_\infty}$ is to take account of the possibility that the stopping time can be infinite, and it ensures that ${A=A\cap\{\tau\le\infty\}\in\mathcal{F}_\infty}$ . From this definition, a random variable ${U}$ us ${\mathcal{F}_\tau}$ -measurable if and only if ${1_{\{\tau\le t\}}U}$ is ${\mathcal{F}_t}$ -measurable for all times ${t\in{\mathbb R}_+\cup\{\infty\}}$ .

Similarly, we can ask what is the set of events observable strictly before the stopping time. For any time ${t}$ , then this sigma-algebra should include ${\mathcal{F}_t}$ restricted to the event ${\{t<\tau\}}$ . This suggests the following definition,

$\displaystyle \mathcal{F}_{\tau-}=\sigma\left(\left\{ A\cap\{t<\tau\}\colon t\ge 0,A\in\mathcal{F}_t \right\}\cup\mathcal{F}_0\right).$

The notation ${\sigma(\cdot)}$ denotes the sigma-algebra generated by a collection of sets, and in this definition the collection of elements of ${\mathcal{F}_0}$ are included in the sigma-algebra so that we are consistent with the convention ${\mathcal{F}_{0-}=\mathcal{F}_0}$ used in these notes.

With these definitions, the question of whether or not a process ${X}$ is ${\mathcal{F}_\tau}$ -measurable at a stopping time ${\tau}$ can be answered. There is one minor issue here though; stopping times can be infinite whereas stochastic processes in these notes are defined on the time index set ${{\mathbb R}_+}$ . We could just restrict to the set ${\{\tau<\infty\}}$ , but it is handy to allow the processes to take values at infinity. So, for the moment we consider a processes ${X_t}$ where the time index ${t}$ runs over ${\bar{\mathbb R}_+\equiv{\mathbb R}_+\cup\{\infty\}}$ , and say that ${X}$ is a predictable, optional or progressive process if it satisfies the respective property restricted to times in ${{\mathbb R}_+}$ and ${X_\infty}$ is ${\mathcal{F}_\infty}$ -measurable.

Lemma 1 Let ${X}$ be a stochastic process and ${\tau}$ be a stopping time.

If ${X}$ is progressively measurable then ${X_\tau}$ is ${\mathcal{F}_\tau}$ -measurable.

If ${X}$ is predictable then ${X_\tau}$ is ${\mathcal{F}_{\tau-}}$ -measurable.

Continue reading “Sigma Algebras at a Stopping Time” →

Stopping Times and the Debut Theorem

In the previous two posts of the stochastic calculus notes, I began by introducing the basic concepts of a stochastic process and filtrations. As we often observe stochastic processes at a random time, a further definition is required. A stopping time is a random time which is adapted to the underlying filtration. As discussed in the previous post, we are working with respect to a filtered probability space ${(\Omega,\mathcal{F},\{\mathcal{F}_t\}_{t\ge 0},{\mathbb P})}$ .

Definition 1 A stopping time is a map ${\tau\colon\Omega\rightarrow{\mathbb R}_+\cup\{\infty\}}$ such that ${\{\tau\le t\}\in\mathcal{F}_t}$ for each ${t\ge 0}$ .

This definition is equivalent to stating that the process ${1_{[\tau,\infty)}}$ is adapted. Equivalently, at any time ${t}$ , the event ${\{\tau\le t\}}$ that the stopping time has already occurred is observable.

One common way in which stopping times appear is as the first time at which an adapted stochastic process hits some value. The debut theorem states that this does indeed give a stopping time.

Theorem 2 (Debut theorem) Let ${X}$ be an adapted right-continuous stochastic process defined on a complete filtered probability space. If ${K}$ is any real number then ${\tau\colon\Omega\rightarrow{\mathbb R}_+\cup\{\infty\}}$ defined by

$\displaystyle \tau(\omega)=\inf\left\{t\in{\mathbb R}_+\colon X_t(\omega)\ge K\right\}$ (1)

is a stopping time.

Continue reading “Stopping Times and the Debut Theorem” →

Filtrations and Adapted Processes

In the previous post I started by introducing the concept of a stochastic process, and their modifications. It is necessary to introduce a further concept, to represent the information available at each time. A filtration ${\{\mathcal{F}_t\}_{t\ge 0}}$ on a probability space ${(\Omega,\mathcal{F},{\mathbb P})}$ is a collection of sub-sigma-algebras of ${\mathcal{F}}$ satisfying ${\mathcal{F}_s\subseteq\mathcal{F}_t}$ whenever ${s\le t}$ . The idea is that ${\mathcal{F}_t}$ represents the set of events observable by time ${t}$ . The probability space taken together with the filtration ${(\Omega,\mathcal{F},\{\mathcal{F}_t\}_{t\ge 0},{\mathbb P})}$ is called a filtered probability space.

Given a filtration, its right and left limits at any time and the limit at infinity are as follows

$\displaystyle \mathcal{F}_{t+}=\bigcap_{s>t}\mathcal{F}_s,\ \mathcal{F}_{t-}=\sigma\Big(\bigcup_{s<t}\mathcal{F}_s\Big),\ \mathcal{F}_{\infty}=\sigma\Big(\bigcup_{t\in{\mathbb R}_+}\mathcal{F}_t\Big).$

Here, ${\sigma(\cdot)}$ denotes the sigma-algebra generated by a collection of sets. The left limit as defined here only really makes sense at positive times. Throughout these notes, I define the left limit at time zero as ${\mathcal{F}_{0-}\equiv\mathcal{F}_0}$ . The filtration is said to be right-continuous if ${\mathcal{F}_t=\mathcal{F}_{t+}}$ . Continue reading “Filtrations and Adapted Processes” →

Stochastic Processes, Indistinguishability and Modifications

I start these notes on stochastic calculus with the definition of a continuous time stochastic process. Very simply, a stochastic process is a collection of random variables ${\{X_t\}_{t\ge 0}}$ defined on a probability space ${(\Omega,\mathcal{F},{\mathbb P})}$ . That is, for each time ${t\ge 0}$ , ${\omega\mapsto X_t(\omega)}$ is a measurable function from ${\Omega}$ to the real numbers.

Stochastic processes may also take values in any measurable space ${(E,\mathcal{E})}$ but, in these notes, I concentrate on real valued processes. I am also restricting to the case where the time index ${t}$ runs through the non-negative real numbers ${{\mathbb R}_+}$ , although everything can easily be generalized to other subsets of the reals.

A stochastic process ${X\equiv\{X_t\}_{t\ge 0}}$ can be viewed in either of the following three ways.

As a collection of random variables, one for each time ${t\ge 0}$ .
As a path
$\displaystyle \setlength\arraycolsep{2pt} \begin{array}{rl} &\displaystyle {\mathbb R}_+\rightarrow{\mathbb R},\smallskip\\ &\displaystyle t\mapsto X_t(\omega), \end{array}$

one for each ${\omega\in\Omega}$ . These are referred to as the sample paths of the process.
As a function from the product space
$\displaystyle \setlength\arraycolsep{2pt} \begin{array}{rl} &\displaystyle {\mathbb R}_+\times\Omega\rightarrow{\mathbb R},\smallskip\\ &\displaystyle (t,\omega)\mapsto X_t(\omega). \end{array}$

Continue reading “Stochastic Processes, Indistinguishability and Modifications” →

	Anonymous on Spitzer’s Formula
	Anonymous on Spitzer’s Formula
	Anonymous on Brownian Bridges
	Anonymous on Spitzer’s Formula
	Anonymous on Spitzer’s Formula
	Anonymous on Spitzer’s Formula
	Anonymous on Spitzer’s Formula
	Anonymous on Spitzer’s Formula
	Anonymous on Spitzer’s Formula
	Anonymous on Spitzer’s Formula