The previous two posts described the behaviour of standard Brownian motion under stochastic changes of time and equivalent changes of measure. I now demonstrate some applications of these ideas to the study of stochastic differential equations (SDEs). Surprisingly strong results can be obtained and, in many cases, it is possible to prove existence and uniqueness of solutions to SDEs without imposing any continuity constraints on the coefficients. This is in contrast to most standard existence and uniqueness results for both ordinary and stochastic differential equations, where conditions such as Lipschitz continuity is required. For example, consider the following SDE for measurable coefficients and a Brownian motion B
| (1) |
If a is nonzero, is locally integrable and b/a is bounded then we can show that this has weak solutions satisfying uniqueness in law for any specified initial distribution of X. The idea is to start with X being a standard Brownian motion and apply a change of time to obtain a solution to (1) in the case where the drift term b is zero. Then, a Girsanov transformation can be used to change to a measure under which X satisfies the SDE for nonzero drift b. As these steps are invertible, every solution can be obtained from a Brownian motion in this way, which uniquely determines the distribution of X.
A standard example demonstrating the concept of weak solutions and uniqueness in law is provided by Tanaka’s SDE
| (2) |
with the initial condition . Here, sgn(x) is defined to be 1 for
and -1 for
. As any solution to this is a local martingale with quadratic variation
Lévy’s characterization implies that X is a standard Brownian motion. This completely determines the distribution of X, meaning that uniqueness in law is satisfied. However, there are many different solutions to (2). In particular, whenever X is a solution then –X will be another one. So, even though all solutions have the same distribution, pathwise uniqueness fails. Next, it is possible to construct a filtered probability space and Brownian motion B such that (2) has a solution. Simply let X be a Brownian motion and set which, again using Lévy’s characterization, implies that B is a Brownian motion. Solutions such as this, which are defined on some filtered probability space rather than an initial specified space are known as weak solutions. In fact, it is not hard to demonstrate that (2) does not have a solution on the filtration
generated by B. As
is invariant under replacing X by –X, it follows that the sets
are X-measurable and invariant under changing the sign of X. In particular, X itself will not be
-measurable, so no solutions to (2) can exist on such a probability space. If weak solutions to an SDE exist, then they can be constructed on an enlargement of the underlying filtered probability space but not, in general, on the original space.
Changes of Time
Consider the 1-dimensional SDE
| (3) |
for measurable and a Brownian motion B. We suppose that X and B are defined on some filtered probability space
. As X is a continuous local martingale, it is a time-changed Brownian motion. That is, there exists a Brownian motion W adapted to some other filtration
such that
(possibly requiring an enlargement of the probability space). Furthermore,
so, by the independent increments property, W and
are independent. It is possible to express X entirely in terms of
and W. First, the quadratic variation of X is,
If it is assumed that a is never zero, then a change of variables together with the identity gives the following
Therefore, is the unique time at which the strictly increasing process
hits the value t. This shows that any solution X to SDE (3) can be written as
| (4) |
for a Brownian motion W independent of . So, the distribution of X satisfying (3) is uniquely determined by the distribution of
.
We can also try going in the opposite direction. That is, if W is a Brownian motion independent from a random variable , then does the process defined by (4) solve our SDE? As long as
is almost surely finite for each time t and
, the answer is yes. In this case, let
be the filtration generated by
and W, and define the stopping times
. Then,
is a local martingale with quadratic variation . So,
is a local martingale. Consider the continuous time change
,
and
. Then, B and
are
-local martingales and, by Lévy’s characterization, B is a Brownian motion. Applying the time change to the stochastic integral gives
and (3) is indeed satisfied.
Under some fairly weak conditions on a, we have shown that the SDE (3) has a solution for a Brownian motion B defined on some filtered probability space. As demonstrated by Tanaka’s SDE above, there isn’t necessarily a solution defined on any given space containing a Brownian motion B. This kind of solution to a stochastic differential equation is called a weak solution.
Definition 1 Consider the n-dimensional stochastic differential equation
(5) (i=1,2,…,n) for a standard m-dimensional Brownian motion
and measurable functions
.
For any probability measure
on
, a weak solution to SDE (5) with initial distribution
is a continuous adapted process
defined on some filtered probability space
such that
and (5) is satisfied for some
-Brownian motion B.
The solution to (5) is said to be unique in law if, for any probability measure
on
, all weak solutions X with
have the same distribution.
Using these definitions, the argument above can be completed to get the following existence and uniqueness results for solutions to the original SDE (3).
Theorem 2 Suppose that
is a measurable and nonzero function such that
is locally integrable. Then, SDE (3) has weak solutions satisfying uniqueness in law.
Proof: The argument given above proves uniqueness in law. Also, setting for a random variable
and independent Brownian motion W, the above construction provides a weak solution with initial value
, provided that the process
is finite and increases to infinity as
. To show that this is indeed the case, consider the following identity
| (6) |
where , which holds for any continuous function
and continuous semimartingale M. As F is twice continuously differentiable with
, this is just Ito’s lemma. A straightforward application of the monotone class theorem extends (6) to all bounded measurable f and, then, by monotone convergence to all nonnegative and locally integrable f.
In particular, if as above, then
and setting
in (6) shows that
is almost surely finite. As f is nonnegative, F will also be nonnegative. So, the local martingale
has the following bound
In the event that , L is bounded below and, by martingale convergence,
exists. In that case,
converges to a finite limit as
. This has zero probability unless F is constant due to the recurrence of Brownian motion (it hits every real value at arbitrarily large times). Furthermore,
is strictly positive, so F is strictly convex and, in particular, is not constant. So, we have shown that
, and the construction of weak solutions given above applies here. ⬜
Changes of Measure
In the previous section, time-changes were applied to construct weak solutions to (3). Alternatively, changes of measure can be used to transform the drift term of stochastic differential equations. Consider the following n-dimensional SDE
| (7) |
(i=1,2,…,n) for a standard m-dimensional Brownian motion and measurable functions
. Suppose that a weak solution has been constructed on some filtered probability space
. Choosing any bounded measurable
(j=1,2,…,m) the idea is to apply a Girsanov transformation to obtain a new measure
under which B gains drift c(t,X). That is
| (8) |
for a -Brownian motion
. Then, looking from the perspective of
, X is a solution to
| (9) |
where . That is, a Girsanov transformation can be used to change the drift of the SDE.
Although this idea is simple enough, there are technical problems to be overcome. To construct the Girsanov transformation, we first define the local martingales
| (10) |
If U is a uniformly integrable martingale then would have the required property. Unfortunately, this condition is not satisfied in many cases. Consider, for example, the simple case where
and c is a nonzero constant. Then, B is a 1-dimensional Brownian motion and is recurrent (hits every value at arbitrarily large times) with probability 1. However, under the transformed measure
, B will be a Brownian motion plus a constant nonzero drift, and tends to plus or minus infinity with probability one, hence is not recurrent. So, the desired measure
cannot be equivalent to
.
The solution is to construct locally. That is, for each time
, construct a measure
such that (8) holds over the interval [0,T]. By Novikov’s criterion, the stopped process
is a uniformly integrable martingale (equivalently, U is a martingale). Indeed,
is bounded, so
is integrable. Then, define the measure
on
by
.
Note that if and
then, applying the martingale property for U,
So, . We would like to imply the existence of a measure
satisfying
for all times
. For such a result to hold, it is necessary to restrict consideration to certain special filtered probability spaces so that Kolmogorov’s extension theorem can be used.
Lemma 3 For some
, let
be the space of continuous functions from
to
, and let Y be the coordinate process,
(
). Furthermore, let
be the sigma algebra on
generated by
and set
.
Suppose that, for each
,
is a probability measure on
and that
whenever
. Then, there is a unique measure
on
satisfying
for all T.
The superscript 0 is used here to signify that the filtration is not complete. That is, we do not add all zero probability sets of
to the filtration (no probability measure has been defined yet, so this wouldn’t even make any sense). This means that care should be taken when applying results from stochastic calculus, as completeness is often assumed. However, it is only really needed to guarantee cadlag versions of martingales and stochastic integrals, which we do not need to be too concerned about for the moment.
Proof: Let be the space of all functions
, with coordinate process
and filtration
. Under the inclusion
,
induces a measure
on
. Since
for all
, these measures are consistent. So, Kolmogorov’s extension theorem says that there exists a measure
on
such that
. By construction,
has a continuous modification over the bounded intervals
so, taking the limit
,
has a continuous modification,
on
. This defines a measurable map
, inducing the required measure
on
. By definition,
is uniquely determined on the algebra
generating
so, by the monotone class theorem, this uniquely determines
. ⬜
We can always restrict consideration to spaces of continuous functions when looking for weak solutions of SDEs.
Lemma 4 Suppose that (7) has a weak solution. Then, there exists a weak solution, with the same initial distribution, on the filtration
defined by Lemma 3.
Proof: Let be a weak solution defined on some filtered probability space
, with respect to the continuous m-dimensional Brownian motion B. Then,
is a continuous (m+n)-dimensional process. Taking d=m+n, and letting
be as in Lemma 3, Z defines a map from
to
and we can define
to be the induced measure
on
. The coordinate process of
can be written as
, where
and
. So,
has the same joint distribution as
and
is a weak solution to the SDE with respect to the Brownian motion
. ⬜
Putting this together enable us to apply the required Girsanov transformation locally, transforming the drift of our SDE.
Lemma 5 Let
be a weak solution to the SDE (7) for an m-dimensional Brownian motion B, and defined on the filtered probability space
, where
are as in Lemma 3. For bounded measurable functions
, let U be the martingale defined by (10).
Then, there is a unique probability measure
on
such that
for each
. The process
defined by (8) is a
-Brownian motion and X is a solution to the SDE (9).
Proof: As shown above, U is a martingale and the measures satisfy the condition
for
. So, Lemma 4 gives a unique measure
such that
as required.
Next, by the theory of Girsanov transformations, the stopped processes are
-local martingales, so
is a
-local martingale. Furthermore, as
is equivalent to
over finite time horizons, the covariations
agree under the
and
measures so, by Lévy’s characterization,
is a
-Brownian motion. Finally, the SDE (9) follows from substituting expression (8) for
into (7). ⬜
We can now prove weak existence and uniqueness in law for SDEs with transformed drift term.
Theorem 6 Let
be measurable functions (i=1,…,n, j=1,…,m) such that
are bounded. Setting
, consider the SDE
(11) Then,
- (11) has a weak solution for any given initial distribution
for
if and only if (7) does.
- (11) satisfies uniqueness in law for any given initial distribution
for
if and only if (7) does.
Proof: By Lemma 4, it is only necessary to use the space and filtration
defined in Lemma 3 when considering weak solutions to the SDE.
Suppose that X is a weak solution to (7) with respect to an m-dimensional Brownian motion B under probability measure . Then, the transformed measure
defined by Lemma 5 makes
into a Brownian motion, with respect to which X satisfies (7). Therefore, under
, X is a weak solution to (11). Also,
so X has the same initial distribution under
and
. This shows that weak existence for (7) implies weak existence for (11). The converse statement follows by exchanging the roles of
and
, and replacing
by
.
Now suppose that (11) satisfies uniqueness in law for solutions with initial distribution , and let X be a weak solution to (7) with
, with respect to m-dimensional Brownian motion B under a measure
. As above, X is a weak solution to (11) under the transformed measure
with the same initial distribution as under
. So, by uniqueness in law, the distribution of X under
is uniquely determined. Also,
can be replaced by
for bounded measurable functions
satisfying
without affecting the conclusion of the theorem. So, by orthogonal projection onto the row-space of
, we can suppose that
for some
. Furthermore, it is not hard to see that
can be constructed as a measurable function from
. So, the local martingale M defined by (10) can be written as
This expresses M, and hence U, entirely in terms of the process X under measure , which is uniquely determined due to uniqueness in law of (11). This uniquely defines the measure
, since
for all and
. So, (7) also satisfies uniqueness in law for the given initial distribution of X. The converse statement follows by exchanging the roles of
and
and replacing
by
. ⬜
Finally, this result allows us to prove weak existence and uniqueness in law for the SDE mentioned at the top of the post.
Theorem 7 Let
and
be measurable functions such that a is nonzero,
is locally integrable and
is bounded. Then, the SDE
(12) (for Brownian motion B) has weak solutions satisying uniqueness in law.
Proof: Theorem 2 guarantees weak existence and uniqueness in law for the SDE (3) with zero drift term. Then, is bounded and measurable, so Theorem 6 extends this to give weak existence and uniqueness in law for SDE (12) with drift
. ⬜
Change of time. . A solution of this is
. A solution of this is 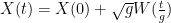
Consider the SDE
1) Is the above statement correct?
2) How do we use this fact to solve another problem, such as this:
where, perhaps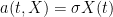 .
.
Hi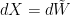 where
where  is the time-changed Brownian motion
is the time-changed Brownian motion 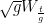 .
. you need to use a random time-change. If
you need to use a random time-change. If  is independent of t, then a weak solution is given by equation (4) in my post. That is,
is independent of t, then a weak solution is given by equation (4) in my post. That is,  where
where
1) It is correct as long as you mean “weak solution”. X will satisfy the SDE
2) To solve
If also depends on time then it is more difficult and the time-change technique does not work as well. You can go through the same steps as in my post and, instead of (4), you get the following
also depends on time then it is more difficult and the time-change technique does not work as well. You can go through the same steps as in my post and, instead of (4), you get the following
I changed variables in the post to solve for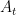 in (4), but it doesn’t work here because of the dependency on s inside the integral. In differential form
in (4), but it doesn’t work here because of the dependency on s inside the integral. In differential form
This replaces the SDE by an ODE, but it doesn’t have an explicit solution. Whether solutions exist and are unique is also unclear.
Sorry, missed your last line “where perhaps “. In this case,
“. In this case,  is independent of
is independent of 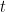 , so the method described in my post solves it.
, so the method described in my post solves it.
Thank you for your quick reply. Also I am unclear about how to post LaTex so that it looks nice.
Anyway perhaps you can help me as I am struggling a little with this.
Consider the SDE
So in the notation given in the text, we have
Can you please elaborate on the next step? (Again I thank you very much.)
To post latex in a comment, use $latex … $ (must include the space after “latex”), and put regular latex between these tags. For “display mode” maths, use the latex keyword \displaystyle and, to center the equation, put between <p align="center"> … </p> html tags. I edited the maths in your posts.
So it seems that the next step is to say
which in this example is
…and how on earth do we approach this integral?
It is unnecessary to use time changes for the specific case of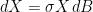 . This can be solved exactly, using Ito’s lemma. Just rewrite the SDE in terms of
. This can be solved exactly, using Ito’s lemma. Just rewrite the SDE in terms of  ,
, 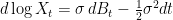 . The solution is the well-known formula for geometric Brownian motion,
. The solution is the well-known formula for geometric Brownian motion,  .
.
The time change method is best suited to cases where there is no such exact formula, and its strength lies in generating (weakly) unique solutions even for non-continuous diffusion coefficients. Solving the integral
cannot be done analytically. We know that it does have a unique solution —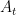 is just the unique time at which the integral on the LHS hits t. You can’t write it in any significantly simpler form.
is just the unique time at which the integral on the LHS hits t. You can’t write it in any significantly simpler form.
Ok, let’s try a different example. Consider the Arithmetic Brownian Motion SDE. I realize this is also probably unnecessarily approached in this way, but I’d like to make sure I understand this.
Then we have
which in this case is just
or
So we have
Is this the correct approach?
Oops sorry about the formatting. ([George]: Fixed, formatting should be fine now) So from above we have
This makes sense to me. Do you think I have the right idea?
Yes! That all looks right!
Now let’s try the following:
and
means
which is
and hence
so we obtain
Does this seem right?
No, there is a mistake here. The formulas work out a bit differently from in my post, because you now have time dependent coefficients. The formula I used to derive (4) is![\int_0^ta(s,X_s)^{-2}\,d[X]_s=t](https://s0.wp.com/latex.php?latex=%5Cint_0%5Eta%28s%2CX_s%29%5E%7B-2%7D%5C%2Cd%5BX%5D_s%3Dt&bg=ffffff&fg=000000&s=0&c=20201002) . Substitute in
. Substitute in ![A_t=[X]_t](https://s0.wp.com/latex.php?latex=A_t%3D%5BX%5D_t&bg=ffffff&fg=000000&s=0&c=20201002) and
and  ,
,
To arrive at (4) I substituted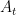 for t and used the substitution $u=latex A_s$ in the integral. This worked fine when
for t and used the substitution $u=latex A_s$ in the integral. This worked fine when  is time-independent, because
is time-independent, because  appears in the integral, but never s on its own. Now, including the time dependency gives
appears in the integral, but never s on its own. Now, including the time dependency gives
The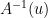 term messes this up a bit. It’s easiest not to do the substitution and instead use
term messes this up a bit. It’s easiest not to do the substitution and instead use
This has A on both sides so it doesn’t give us an explicit solution in general. However, in your case, works out fine.
works out fine.
giving,
I see, this solution matches what we know about Ornstein-Uhlenbeck vis-a-vis Ito.
I’m grateful for your help. You’ve been very generous with your knowledge – and also forgiving about the LaTex / formatting issues!!
Thanks a million.
No problem!
hi, George
The approach in this page is very interesting.
Would you give a reference, which book/article it is based?
Thank you.
This post is applying fairly standard techniques that I have seen in several places. I’m not at home to look this up right now, but I’m pretty sure that both the books by Revuz-Yor and Rogers-Williams use the time change method for 1 dimensional diffusions, and also the measure change method (in arbitrary dimensions). The measure change was also used by Stroock-Varadhan to quickly reduce their well known uniqueness result to one without drift.
Thank you very much for several references.
Dear George:
In the proof of Theorem 2, Why is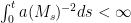 almost surely, provided that
almost surely, provided that 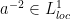 ? Thank you.
? Thank you.
I just find an answer to myself, please verify: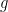 is continuous, then
is continuous, then 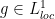 , and
, and  is closed under composition. Hence, because
is closed under composition. Hence, because  ,
, 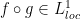 .
.
If
No, that’s not correct,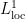 is not closed under composition. Theorem 2 only works because M is a semimartingale with quadratic variation
is not closed under composition. Theorem 2 only works because M is a semimartingale with quadratic variation ![d[M]_t=dt](https://s0.wp.com/latex.php?latex=d%5BM%5D_t%3Ddt&bg=ffffff&fg=000000&s=0&c=20201002) , and then equation (6) is applied.
, and then equation (6) is applied.
Dear George,
Here is my understanding:
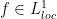 is required to have
is required to have 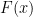 is well defined.
is well defined.
So, Ito identity (6) makes sense, and it implies all terms in (6) are a.s. finite.
Thank you very much.
Hi George,
First congrats for this very nice blog, where things in the literature are made edible for somebody not trained in a pure probability playground (I am a physicist…).
In the SDE (3), , I was wondering how crucial is the condition you mention that
, I was wondering how crucial is the condition you mention that  is never zero. What I have in mind is the so-called Kimura’s diffusion where
is never zero. What I have in mind is the so-called Kimura’s diffusion where 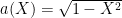 : the state space is the interval
: the state space is the interval ![I=[-1,1]](https://s0.wp.com/latex.php?latex=I%3D%5B-1%2C1%5D&bg=ffffff&fg=000000&s=0&c=20201002) (starting from
(starting from  within it), and it is known that that the solution hits either ±1 in a finite mean time and stays there forever.
within it), and it is known that that the solution hits either ±1 in a finite mean time and stays there forever. , with
, with  . Then by Itô’s formula
. Then by Itô’s formula
Related question related to a possible time-change: set
Does there exist a change of time which allows to rewrite
which allows to rewrite
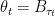 ?
?![{\rm Proba}[X_t=x|X_0=x_0]](https://s0.wp.com/latex.php?latex=%7B%5Crm+Proba%7D%5BX_t%3Dx%7CX_0%3Dx_0%5D&bg=ffffff&fg=000000&s=0&c=20201002) ?
?
How is this useful to say recover the known expression for the conditional transition
probability distribution function
Best,
Ivan Dornic
Hi Ivan,
Thanks for your comment. I assumed that is never zero for simplicity here. The aim of this post was really to demonstrate the techniques of time and measure changes rather than give as general as possible a statement on the solutions to SDEs.
is never zero for simplicity here. The aim of this post was really to demonstrate the techniques of time and measure changes rather than give as general as possible a statement on the solutions to SDEs.
Anyway, if does hit zero, then there are several possibilities for the SDE
does hit zero, then there are several possibilities for the SDE 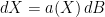 , which can also be handled by the time change method.
, which can also be handled by the time change method.
i)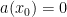 for some value of x0, but
for some value of x0, but 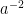 is still locally integrable (so that
is still locally integrable (so that  can only vanish on a set of measure zero). In this case, there exist solutions to the SDE, but they are not unique. For example, consider
can only vanish on a set of measure zero). In this case, there exist solutions to the SDE, but they are not unique. For example, consider  . Then
. Then 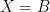 satisfies this. However, letting X equal B but stopped at some time when it hits zero will give another solution. If you require that the set
satisfies this. However, letting X equal B but stopped at some time when it hits zero will give another solution. If you require that the set 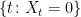 has zero lebesgue measure, then the solution is unique.
has zero lebesgue measure, then the solution is unique.
ii) and
and 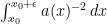 are both infinite. In this case there is a unique solution, but the boundary is not accessible (unless you start the process at the boundary, in which case it stays there).
are both infinite. In this case there is a unique solution, but the boundary is not accessible (unless you start the process at the boundary, in which case it stays there).
iii) is finite but
is finite but 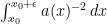 is infinite. Here, we still have uniqueness in law. In this case the boundary is accessible from below (but not above), and is absorbing. This is the case for the upper boundary
is infinite. Here, we still have uniqueness in law. In this case the boundary is accessible from below (but not above), and is absorbing. This is the case for the upper boundary  in your example.
in your example.
iv) As with (iii), but where the boundary is accessible from above.
These situations are handled by the time change method. For example, consider my expression (4) in the post, in case (iii). As the Brownian motion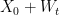 approaches
approaches 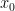 from above at some time
from above at some time  , the integral of
, the integral of  diverges so, inverting this,
diverges so, inverting this, 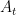 approaches
approaches  but never reaches it. This implies that the processes
but never reaches it. This implies that the processes  approaches
approaches 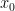 from above, but never reaches it in finite time. On the other hand, as
from above, but never reaches it in finite time. On the other hand, as 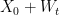 approaches
approaches 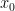 from below the integral of
from below the integral of  is bounded, but diverges immediately after
is bounded, but diverges immediately after  . So,
. So,  approaches time
approaches time  in finite time, then jumps to infinity. Applying the time change, the solution
in finite time, then jumps to infinity. Applying the time change, the solution 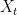 hits
hits 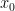 and stays there.
and stays there.
In your example, , the process can hit either 1 or -1 in finite time, and always will hit one of these as, under the time change, it is just a Brownian motion which will hit -1 or 1.
, the process can hit either 1 or -1 in finite time, and always will hit one of these as, under the time change, it is just a Brownian motion which will hit -1 or 1.
[btw, I edited the latex in your post].
And, for your second question. You can time-change X to a Brownian motion (stopped when it hits ±1) because it is a continuous local martingale. However, theta is not. Your displayed expression shows that it has a drift term (I think you have a typo in your formula?). You could transform it to a Brownian motion stopped at ±π/2 by a measure change to remove the drift – that is, a Girsanov transform as discussed in this post. I’m not sure how well it works out for explicitly computing the conditional probabilities though. You will get an expectation of an exponential term involving the drift term, which is probably rather messy (but I haven’t tried). Adding a constant drift via Girsanov transforms is easy though and is one way to compute the probability of BM with drift hitting a barrier.
(I think you have a typo in your formula?). You could transform it to a Brownian motion stopped at ±π/2 by a measure change to remove the drift – that is, a Girsanov transform as discussed in this post. I’m not sure how well it works out for explicitly computing the conditional probabilities though. You will get an expectation of an exponential term involving the drift term, which is probably rather messy (but I haven’t tried). Adding a constant drift via Girsanov transforms is easy though and is one way to compute the probability of BM with drift hitting a barrier.
Hope that helps!
i have some various question
so first how we can get this :
$$
e^{bt} \ \int_0^t \ f(s) ds=\int_0^t \ ( e^{-bs} \ f(s)-be^{-bs}\int_0^s\ f(u)\ du) \ ds
$$
i need explanation in details please
Second question if we have stopping time and X is stochastic processus in Rn
$$
T=inf ( { t>=0 , X_{s \wedge T}^2 + Y _{s \wedge T}^2 >= A }) \ \ or \\
T=inf ( { t>=0 , | X_t | \geq A + | Y _t | \geq A } )
$$ so how we can prove that :
$$
\ {E}(| X _{s \wedge T} – Y _{s \wedge T} |^2) \leq \propto
$$
is finite
The third question how we can get that :
$$-\int_0^t \ sgn(X_{s}) \ dB_{s}=\int_0^t \ sgn(-X_{s})\ dB_{s}+2\int_0^t 1_{X_{s} =0}dB_{s}$$
with B is brownian motion on Rn ,and sgn is Sign function
i took this from Tanaka ‘s SDE to prove that there ‘s non pathwise uniquenss
so please if you have examle of SDE that has strong solution without strong uniquenss (pathwise uniquenss)
Thanks for Your time
i’ll be grateful for ur help
best,
Educ
Hi There is a little typo in theorem 6 where it should be c_i and not b_i regards
To be more precise I meant c_i.a_{ij} instead of b_i.a_{ij} in the seting of \tilda[b_i}
Hi George, again I have several questions regarding the details of the proofs. I would greatly appreciate if you could help me understand them.
1. In the proof of Theorem 2, how does the identity for F(M_t) extends to nonnegative locally integrable functions f by monotone convergence? The application of the monotone class theorem part seems to follow from the fact that continuous functions approximate bounded measurable functions and monotone class theorem involves bounded monotone limits, so dominated convergence theorems for Lebesgue Stieltjes integral and stochastic integrals apply on all terms of the identity.
However, I am not aware of any approximation results for locally integrable functions via bounded measurable functions. To use monotone convergence, as F itself is defined in terms of Lebesgue integral and we have a stochastic integral and L-S integral on the Right hand side terms, we would need to use dominated or bounded convergence theorems on the RHS and on the LHS to extend the identity.
Moreover, I do not know why f being locally integrable would give the integrability of \int_0^t F'(M)dM and \int_0^t f(M)d[M] in the first place.
2. In the proof of Lemma 3, I think you are taking Y’ to be the image of Y under the inclusion map defined from the continuous function space. And extend Y’ to [0,\infty) from [0,T]. But how does this define a map from all of \Omega’, which is just the space of all functions R_+ \to R^d to C(R_+,R^d)? I don’t understand how we get a continuous modification for every function R_+ \to R^d from the construction here. And why does this map become measurable?
3. In the proof of Lemma 4, my understanding is that B’ is the projection map onto the first R^m and X’ is the projection map onto the next R^n space. Then I can see that (B’,X’) ~ (B,X) in distribution, but why does the equivalence of joint distributions and the fact that X is a weak solution imply that X’ is also a weak solution with respect to the Brownian motion B’?
4. Finally, in the proof of Theorem 6, could you explain the sentence “So, by orthogonal projection onto the row-space of a_ij, we can suppose that c_j = \sum_i \lambda_i a_ij for some \lambda_i”? I can’t figure out why we are able to choose c to be some orthogonal projection onto the row-space of a. And why is the \lambda_i constructed this way measurable?
Thank you
Hi
who can solve the equation dxt=(Q1- Q2 ) xt dt+ Q3 dwt by using change measure