The Monotone Class Theorem

The monotone class theorem, and closely related ${\pi}$ -system lemma, are simple but fundamental theorems in measure theory, and form an essential step in the proofs of many results. General measurable sets are difficult to describe explicitly so, when proving results in measure theory, it is often necessary to start by considering much simpler sets. The monotone class theorem is then used to extend to arbitrary measurable sets. For example, when proving a result about Borel subsets of ${{\mathbb R}}$ , we may start by considering compact intervals and then apply the monotone class theorem. I include this post on the monotone class theorem for reference.

We start with some definitions. Given a collection ${\mathcal E}$ of subsets of a set ${E}$ , we use the notation ${A^c=E\setminus A}$ for the complement of ${A\in\mathcal E}$ .

Definition 1 Let ${E}$ be a set. Then, a collection ${\mathcal E}$ of subsets of ${E}$ is a

${\pi}$ -system if and only if ${A\cap B\in\mathcal E}$ for all ${A,B\in\mathcal E}$ .

algebra if and only if

${E\in\mathcal E}$ .

${A^c\in\mathcal E}$ for all ${A\in\mathcal E}$ .

${A\cup B\in\mathcal E}$ for all ${A,B\in\mathcal E}$ .

monotone class if and only if

${\bigcup_n A_n\in\mathcal E}$ for all increasing sequences ${A_1,A_2,\ldots\in\mathcal E}$ .

${\bigcap_n A_n\in\mathcal E}$ for all decreasing sequences ${A_1,A_2,\ldots\in\mathcal E}$ .

d-system (or Dynkin system, or ${\lambda}$ -system) if and only if

${E\in\mathcal E}$ .

${B\setminus A\in\mathcal E}$ for all ${A\subseteq B}$ in ${\mathcal E}$ .

${\bigcup_n A_n\in\mathcal E}$ for all increasing sequences ${A_1,A_2,\ldots\in\mathcal E}$ .

${\sigma}$ -algebra if and only if

${E\in\mathcal E}$ .

${A^c\in\mathcal E}$ for all ${A\in\mathcal E}$ .

${\bigcup_{n=1}^\infty A_n\in\mathcal E}$ for all sequences ${A_n\in\mathcal E}$ .

In short, we can say that a ${\pi}$ -system is closed under pairwise intersections, an algebra is closed under finite set operations, a monotone class is closed under increasing and decreasing limits, a d-system is closed under increasing limits, taking differences with a subset, and contains the whole space, and a ${\sigma}$ -algebra is closed under countable set operations.

There are various simple relations between the definitions given above.

Lemma 2

every algebra is a ${\pi}$ -system.

every d-system is a monotone class.

every ${\sigma}$ -algebra is a ${\pi}$ -system, an algebra, a monotone class and a d-system.

Proof: That an algebra ${\mathcal E}$ is also a ${\pi}$ -system is clear: ${A\cap B=(A^c\cup B^c)^c\in\mathcal E}$ for all ${A,B\in\mathcal E}$ .

For a set ${A}$ in a d-system ${\mathcal E}$ , its complement ${A^c=E\setminus A}$ is also in ${\mathcal E}$ . So, for a decreasing sequence ${A_n\in\mathcal E}$ , writing ${\bigcap_nA_n=\left(\bigcup_nA_n^c\right)^c\in\mathcal E}$ shows that ${\mathcal E}$ is also a monotone class.

Now, suppose that ${\mathcal E}$ is a ${\sigma}$ -algebra. For any ${A,B\in\mathcal E}$ , define a sequence ${A_n}$ by ${A_1=A}$ and ${A_n=B}$ for ${n > 1}$ . Then, ${A\cup B=\bigcup_nA_n}$ is in ${\mathcal E}$ , so ${\mathcal E}$ is an algebra and, hence, also a ${\pi}$ -system. Next, ${B\setminus A=A^c\cap B\in\mathcal E}$ for all ${A,B\in\mathcal E}$ . So ${\mathcal E}$ is a d-system and, hence, also a monotone class. ⬜

The definitions above are also related by the following equivalent characterizations of ${\sigma}$ -algebras.

Lemma 3 For a collection ${\mathcal E}$ of subsets of ${E}$ , the following are equivalent.

${\mathcal E}$ is a ${\sigma}$ -algebra.

${\mathcal E}$ is both a ${\pi}$ -system and a d-system.

${\mathcal E}$ is both an algebra and a monotone class.

Proof: Lemma 2 states that a ${\sigma}$ -algebra is also a ${\pi}$ -system, an algebra, a monotone class, and a d-system. Only the converse statements remain.

Suppose that ${\mathcal E}$ is both an algebra and a monotone class. If ${A_n}$ is a sequence in ${\mathcal E}$ then each finite union ${B_n=\bigcup_{k=1}^nA_k}$ is also in ${\mathcal E}$ . As ${B_n}$ is increasing, the union ${\bigcup_nA_n=\bigcup_nB_n}$ is in ${\mathcal E}$ , which is therefore a ${\sigma}$ -algebra.

Suppose that ${\mathcal E}$ is both a ${\pi}$ -system and a d-system. By the d-system property, ${A^c=E\setminus A\in\mathcal E}$ for all ${A\in\mathcal E}$ . Hence, ${A\cup B=(A^c\cap B^c)^c\in\mathcal E}$ for ${A,B\in\mathcal E}$ , showing that ${\mathcal E}$ is an algebra. It is also monotone class, by the second statement of lemma 2. Hence, ${\mathcal E}$ is a ${\sigma}$ -algebra. ⬜

By definition, measures are constructed with respect to a ${\sigma}$ -algebra on a set ${E}$ . Precisely, a measure ${\mu\colon\mathcal E\rightarrow{\mathbb R}^+\cup\{\infty\}}$ satisfies countable additivity

$\displaystyle \mu\left(\bigcup\nolimits_nA_n\right)=\sum_n\mu(A_n)$

for sequences ${A_1,A_2,\ldots}$ of pairwise disjoint sets in ${\mathcal E}$ . In some sense, it would be more natural to define measures on d-systems rather than ${\sigma}$ -algebras. This is because any extension of a probability measure from a collection of sets ${\mathcal E}$ to the d-system it generates is unique, by the identities

$\displaystyle \setlength\arraycolsep{2pt} \begin{array}{rl} &\displaystyle\mu(E)=1,\smallskip\\ &\displaystyle\mu(B\setminus A)=\mu(B)-\mu(A),\smallskip\\ &\displaystyle\mu\left(\bigcup\nolimits_n A_n\right)=\lim_{n\rightarrow\infty}\mu(A_n). \end{array}$

(1)

Here, ${A\subseteq B}$ and ${A_n}$ is an increasing sequence of sets. For ${\sigma}$ -algebras, this does not hold. The measures of ${A\cup B}$ and ${A\cap B}$ cannot, in general, be determined just from the measures of ${A}$ and ${B}$ . However, only using d-systems would be much too restrictive. Finite unions and intersections are very simple set operations under which we would want the class of measurable sets should be closed. This is where the ${\pi}$ -system lemma comes in. So long as we start from a ${\pi}$ -system, then the d-system that it generates is already a ${\sigma}$ -algebra.

Given any collection ${\mathcal E}$ of subsets of a set ${E}$ , we refer to the smallest ${\sigma}$ -algebra containing ${\mathcal E}$ as the ${\sigma}$ -algebra generated by ${\mathcal E}$ , and is denoted by ${\sigma(\mathcal E)}$ . Similarly, we can talk about the ${\pi}$ -system, algebra, monotone class, or d-system generated by ${\mathcal E}$ . The following result is known variously as the ${\pi}$ -system lemma, Dynkin’s ${\pi}$ – ${\lambda}$ theorem, or even as the monotone class theorem.

Theorem 4 (Dynkin) Let ${\mathcal E}$ be a ${\pi}$ -system on a set ${E}$ , and ${\mathcal F}$ be a d-system containing ${\mathcal E}$ . Then, ${\sigma(\mathcal E)\subseteq\mathcal F}$ .

In particular, if ${\mathcal F}$ is the d-system generated by ${\mathcal E}$ , then ${\sigma(\mathcal E)=\mathcal F}$ .

Proof: First, suppose that ${\mathcal F}$ is the d-system generated by ${\mathcal E}$ . As ${\sigma}$ -algebras are also d-systems, the inequality ${\mathcal F\subseteq\sigma(\mathcal E)}$ is immediate. Only the reverse inequality needs to be shown.

For any ${C\in\mathcal F}$ , let ${\mathcal F_C}$ denote the collection of sets ${A\in\mathcal F}$ satisfying ${A\cap C\in\mathcal F}$ . If ${A\subseteq B}$ are in ${\mathcal F_C}$ , we have

$\displaystyle (B\setminus A)\cap C=(B\cap C)\setminus(A\cap C)\in\mathcal F,$

so ${B\setminus A\in\mathcal F_C}$ . Next, supposing that ${\{A_n\}_{n=1,2,\ldots}}$ is an increasing sequence in ${\mathcal F_C}$ ,

$\displaystyle \left(\bigcup\nolimits_nA_n\right)\cap C=\bigcup\nolimits_n(A_n\cap C)\in\mathcal F,$

so ${\bigcup_nA_n\in\mathcal F_C}$ . This shows that ${\mathcal F_C}$ is itself a d-system

For ${C\in\mathcal E}$ , the ${\pi}$ -system property immediately gives ${\mathcal E\subseteq \mathcal F_C}$ , so ${\mathcal F_C=\mathcal F}$ . Then, for any ${C\in\mathcal F}$ and ${A\in\mathcal E}$ , we have ${C\in\mathcal F_A}$ or, equivalently, ${A\in\mathcal F_C}$ . This, again, shows that ${\mathcal F_C=\mathcal F}$ . Hence, ${\mathcal F_C=\mathcal F}$ . Therefore, ${A\cap B\in\mathcal F}$ for all ${A,B\in\mathcal F}$ . We have shown that ${\mathcal F}$ is a ${\pi}$ -system and, by lemma 3, is a ${\sigma}$ -algebra. So, ${\sigma(\mathcal E)\subseteq\mathcal F}$ , giving ${\sigma(\mathcal E)=\mathcal F}$ as required.

Finally, let ${\mathcal F}$ be any d-system containing ${\mathcal E}$ . If ${\mathcal F^\prime}$ is the d-system generated by ${\mathcal E}$ then, ${\sigma(\mathcal E)=\mathcal F^\prime\subseteq\mathcal F}$ as required. ⬜

As an immediate application of the ${\pi}$ -system lemma, we show uniqueness of extensions of measures.

Lemma 5 Let ${\mu}$ and ${\nu}$ be probability measures on a measurable space ${(E,\mathcal E)}$ . If they agree on a ${\pi}$ -system generating ${\mathcal E}$ , then ${\mu=\nu}$ .

Proof: Let ${\mathcal F}$ be the set of ${A\in\mathcal E}$ for which ${\mu(A)=\nu(A)}$ . By equations (1) applied to ${\mu}$ and ${\nu}$ , ${\mathcal F}$ is a d-system. As it also contains a ${\pi}$ -system generating the ${\sigma}$ -algebra ${\mathcal E}$ , theorem 4 gives ${\mathcal E\subseteq \mathcal F}$ , so ${\mu=\nu}$ on ${\mathcal E}$ . ⬜

The cumulative distribution function ${F\colon{\mathbb R}\rightarrow{\mathbb R}^+}$ of a probability measure ${\mu}$ on the Borel sigma algebra on the real line is defined by ${F(x)=\mu((-\infty,x])}$ . A common use of the above lemma is the following.

Corollary 6 A probability measure on the standard Borel space on the real line is uniquely determined by its distribution function.

Proof: The standard Borel space is ${({\mathbb R},\mathcal B)}$ , where ${\mathcal B}$ is the Borel ${\sigma}$ -algebra on ${{\mathbb R}}$ . Let ${\mathcal E}$ consist of the intervals ${(-\infty,x]}$ for ${x\in{\mathbb R}}$ . This is a ${\pi}$ -system with ${\sigma(\mathcal E)=\mathcal B}$ . If ${\mu}$ and ${\nu}$ are two finite measures with the same distribution function, then ${\mu((-\infty,x])=\nu((-\infty,x])}$ for all ${x\in{\mathbb R}}$ . So ${\mu}$ and ${\nu}$ agree on ${\mathcal E}$ . Lemma 5 gives ${\mu=\nu}$ . ⬜

I move on to the statement of the monotone class theorem. Here, we weaken the requirements on ${\mathcal F}$ so that it is only required to be a monotone class, rather than the more restrictive d-system requirement used by the ${\pi}$ -system lemma. This is at the expense of requiring the stronger condition that ${\mathcal E}$ is an algebra, and not just a ${\pi}$ -system.

Theorem 7 (Monotone Class Theorem) Let ${\mathcal E}$ be an algebra on a set ${E}$ , and ${\mathcal F}$ be a monotone class containing ${\mathcal E}$ . Then, ${\sigma(\mathcal E)\subseteq\mathcal F}$ .

In particular, if ${\mathcal F}$ is the monotone class generated by ${\mathcal E}$ , then ${\sigma(\mathcal E)=\mathcal F}$ .

In many cases where the monotone class theorem is used, the collection of sets ${\mathcal E}$ that we start with almost, but not quite, satisfies the definition of an algebra. For example, if it is the closed subsets of a metrizable space, then ${\mathcal E}$ is closed under finite intersections and unions. The complement of a closed set need not be closed, although it is always the limit of an increasing sequence of closed sets. For such cases, the following slightly generalized version can be useful. Note that theorem 7 is an immediate consequence.

We use the notation ${M(\mathcal E)}$ for the monotone class generated by a collection ${\mathcal E}$ of subsets of a set ${E}$ .

Theorem 8 (Monotone Class Theorem) Let ${\mathcal E}$ be a nonempty collections of subsets of ${E}$ such that ${A^c}$ and ${A\cap B}$ are in ${M(\mathcal E)}$ for all ${A,B\in\mathcal E}$ . Then, ${\sigma(\mathcal E)=M(\mathcal E)}$ .

In particular, if ${\mathcal F}$ is a monotone class containing ${\mathcal E}$ then, ${\sigma(\mathcal E)\subseteq\mathcal F}$ .

Proof: As ${\sigma}$ -algebras are also monotone classes, the inequality ${M(\mathcal E)\subseteq\sigma(\mathcal E)}$ is immediate. Only the reverse inequality needs to be shown. Let ${\mathcal F}$ be the collection of ${A\in M(\mathcal E)}$ such that ${A^c}$ is also in ${M(\mathcal E)}$ . By the condition of the theorem, ${\mathcal E\subseteq\mathcal F}$ . If ${A_n\in\mathcal F}$ is an increasing sequence then, by the monotone class property, ${\bigcup_nA_n}$ and

$\displaystyle \left(\bigcup\nolimits_nA_n\right)^c=\bigcap\nolimits_n A_n^c$

are both in ${M(\mathcal E)}$ . So, ${\bigcup_nA_n}$ is in ${\mathcal F}$ , showing that it is closed under taking limits of increasing sequences. Similarly, it is closed under taking limits of decreasing sequences so is a monotone class, giving ${\mathcal F=M(\mathcal E)}$ . Therefore, ${A^c\in M(\mathcal E)}$ for all ${A\in M(\mathcal E)}$ .

Now, for any ${B\in M(\mathcal E)}$ , let ${\mathcal F_B}$ denote the collection of ${A\in M(\mathcal E)}$ such that ${A\cap B}$ is also in ${M(\mathcal E)}$ . For any sequence ${A_n\in\mathcal F_B}$ ,

$\displaystyle \setlength\arraycolsep{2pt} \begin{array}{rl} &\displaystyle\left(\bigcup\nolimits_nA_n\right)\cap B=\bigcup\nolimits_n(A_n\cap B),\smallskip\\ &\displaystyle\left(\bigcap\nolimits_nA_n\right)\cap B=\bigcap\nolimits_n(A_n\cap B). \end{array}$

So, if ${A_n}$ is an increasing or decreasing sequence, its limit is also in ${\mathcal F_B}$ , showing that ${\mathcal F_B}$ is a monotone class. By the condition of the theorem, ${\mathcal E\subseteq \mathcal F_B}$ for any ${B\in\mathcal E}$ , giving ${\mathcal F_B=M(\mathcal E)}$ . Hence, ${A\cap B\in M(\mathcal E)}$ for all ${A\in M(\mathcal E)}$ and ${B\in\mathcal E}$ . This shows that ${\mathcal E\subseteq\mathcal F_A}$ for any ${A\in M(\mathcal E)}$ . Therefore, ${\mathcal F_A=M(\mathcal E)}$ , showing that ${M(\mathcal E)}$ is closed under pairwise intersections.

We have shown that ${M(\mathcal E)}$ is closed under set complements and pairwise intersections. As it is nonempty, this shows that it is an algebra. By lemma 3, it is a ${\sigma}$ -algebra, giving ${\sigma(\mathcal E)\subseteq M(\mathcal E)}$ as required. ⬜

11 thoughts on “The Monotone Class Theorem”

Philipp Wacker says:

12 August 20 at 9:58 PM

I had some trouble with the last part (starting with “For $C\in \mathcal E$ , the $\pi$ -system property…” of the proof of theorem 4 and it took me a while to figure out the exact mechanics of the arguments. I am proposing a slightly extended explanation below. You can of course completely ignore this but maybe some readers would profit from a slightly more detailed explanation.

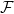For $C\in \mathcal E$ , the $\pi$ -system property immediately gives $E\subset \mathcal F_C$ . Note first that by definition of $\mathcal F_C$ , we have $\mathcal F_C \subset \mathcal F$ for any $C\in \mathcal F$ .

As $\mathcal F$ is the minimal d-system generated by 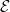$\mathcal E$ and $\mathcal F_C$ is another d-system, we obtain $\mathcal F\subset \mathcal F_C$ , which already implies $\mathcal F_C = \mathcal F$ , but so far only for $C\in \mathcal E$ .

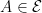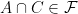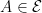Now consider more generally $C\in \mathcal F$ and additionally an $A\in \mathcal E$ . Because of what we just established, we know that $C\in \mathcal F = \mathcal F_A$ , i.e. $C\in \mathcal F_A$ , which just means that $A\cap C\in \mathcal F$ . By symmetry, this implies $A\in \mathcal F_C$ , thus (because $A\in \mathcal E$ was arbitrary), 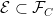$\mathcal E \subset \mathcal F_C$ . By the same argument as above (minimality of the d-system 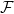$\mathcal F$ ), this again yields $\mathcal F_C = \mathcal F$ , this time for all $C\in \mathcal F$ .

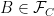This statement implies that for all $B,C\in\mathcal F$ , we know that $B\in \mathcal F_C$ , i.e. $B\cap C\in \mathcal F$ , which is the definition of 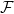$\mathcal F$ being a 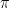$\pi$ -system. By lemma 3 (make link), 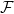$\mathcal F$ is also a $\sigma$ -algebra.

[Rest as in the text]

1. George Lowther says:
  
  14 August 20 at 1:45 PM
  
  Thanks for your suggestion. I will have a reread through the argument when I have some time, and update accordingly.
  
Pingback: Visualization of the Monotone Class Theorem Containment Relations – Colm Bhandal
Pingback: Distribution Function Product Identity for Independent Random Vector Components – Colm Bhandal
Pingback: Independence of Components Implies Independence of Random Vectors – Colm Bhandal
souravmath says:

2 January 21 at 5:45 AM

The link to Borel is broken.

1. souravmath says:
  
  2 January 21 at 5:45 AM
  
  I meant the first hyperlink to Borel sets.
  
  1. George Lowther says:
    
    2 January 21 at 2:04 PM
    
    Fixed. Thanks!
    
Tony says:

28 September 21 at 1:02 PM

Hello!
First of all, you have an amazing blog, thank you very much for your work!

Apart from that, I have some trouble with the proof of Theorem 8.

Basically, we take a monotone class generated by E and prove that it is closed under intersections and complements. However, as far as I understand, one feature is still missing: it is never mentioned that the set E belongs to the corresponding monotone class. In Theorem 7 it holds automatically (due to E being an algebra), but how can we say that E is in M(E)?

Thank you in advance!

1. George Lowther says:
  
  25 February 22 at 2:23 PM
  
  I showed that $M(\mathcal E)$ is closed under set complementation and intersection. As it is nonempty, it contains at least one set A and hence contains $(A\cap A^c)^c=E$ .
  
molecules says:

23 August 22 at 11:37 PM

Suppose $m$ is defined on $\mathcal{E} \subset \mathcal{P}(E)$ and $m(E) < \infty$. It is possible to show if $m_1,m_2$ are two extensions from $\mathcal{E}$ to $\lambda(\mathcal{E})$ then they must be equal, but does an extension exist like it does in in the algebra to $\sigma$-algebra case?

Although the Caratheodory Measurable set condition doesn't work anymore, from $(1)$ it seems $m$ can be constructed iteratively from $\mathcal{E}$ to $\lambda{E}$.

	Anonymous on About
	Anonymous on About
	Anonymous on The Stochastic Integral
	Anonymous on Bessel Processes
	Anonymous on Bessel Processes
	Stat Prof on Pathwise Regularity of Optiona…
	Yang Chu on Spitzer’s Formula
	Anonymous on About
	Anonymous on Continuous Processes with Inde…
	Anonymous on Continuous Processes with Inde…

The Monotone Class Theorem

Published by George Lowther

11 thoughts on “The Monotone Class Theorem”

Leave a comment Cancel reply

Related

Published by George Lowther

11 thoughts on “The Monotone Class Theorem”

Leave a comment Cancel reply