The definition of Markov processes, as given in the previous post, is much too general for many applications. However, many of the processes which we study also satisfy the much stronger Feller property. This includes Brownian motion, Poisson processes, Lévy processes and Bessel processes, all of which are considered in these notes. Once it is known that a process is Feller, many useful properties follow such as, the existence of cadlag modifications, the strong Markov property, quasi-left-continuity and right-continuity of the filtration. In this post I give the definition of Feller processes and prove the existence of cadlag modifications, leaving the further properties until the next post.
The definition of Feller processes involves putting continuity constraints on the transition function, for which it is necessary to restrict attention to processes lying in a topological space . It will be assumed that E is locally compact, Hausdorff, and has a countable base (lccb, for short). Such spaces always possess a countable collection of nonvanishing continuous functions
which separate the points of E and which, by Lemma 6 below, helps us construct cadlag modifications. Lccb spaces include many of the topological spaces which we may want to consider, such as
, topological manifolds and, indeed, any open or closed subset of another lccb space. Such spaces are always Polish spaces, although the converse does not hold (a Polish space need not be locally compact).
Given a topological space E, denotes the continuous real-valued functions vanishing at infinity. That is,
is in
if it is continuous and, for any
, the set
is compact. Equivalently, its extension to the one-point compactification
of E given by
is continuous. The set
is a Banach space under the uniform norm,
We can now state the general definition of Feller transition functions and processes. A topological space is also regarded as a measurable space by equipping it with its Borel sigma algebra
, so it makes sense to talk of transition probabilities and functions on E.
Definition 1 Let E be an lccb space. Then, a transition function
is Feller if, for all
,
.
is continuous with respect to the norm topology on
.
.
A Markov process X whose transition function is Feller is a Feller process.
Note: Feller processes, as defined here, are sometimes referred to as Feller-Dynkin processes (and similarly for Feller transition functions). The term Feller process is sometimes used to refer to the more general class of processes obtained by replacing by the space
of continuous bounded functions in the definition above. I am following the terminology used by Revuz and Yor (Continuous Martingales and Brownian Motion).
The first condition says that, if X is a Feller process and then, the conditional distribution of
depends on
in a continuous sense. Also, as
vanishes at infinity, if S is a compact subset of E, then the probability that
will vanish conditional on
being far away. That is, we can find compact sets
such that
is as small as we like.
Examples of Feller processes include,
- standard Brownian motion, with the transition function
- Poisson processes of rate
, with the transition function
More generally, as we will see in a later post, all -valued processes with stationary independent increments (i.e., Lévy processes) are Feller. In fact, all processes which are continuous in probability and have independent increments, even if they are not stationary, have a Feller space-time process
.
Another situation in which Feller processes arise is from stochastic differential equations. Consider the SDE,
() for an n-dimensional process X, an m-dimensional Brownian motion B, and Lipschitz-continuous functions
. As previously shown, such SDEs have a unique solution for any initial value
. We can then define
to be the distribution of
, in which case X is Markov with transition function
. By continuity of solutions with respect to the initial value x, it can be seen that
will be continuous for
. Next, as the coefficients are Lipschitz, they cannot grow any faster then linearly as
. From this, it can be shown that, by making
large, the probability of
being in some fixed bounded region can be made as small as possible (this can be proven using a similar method as showing that SDEs with linearly bounded coefficients cannot explode). So,
. Furthermore, continuity of such processes implies that
will be a continuous function of t which, as we will show, implies that
is a Feller transition function.
The second condition of Definition 1, that is continuous under the norm topology, can sometimes be quite tricky to prove. Fortunately, this is not necessary, as it turns out to be equivalent to a seemingly much weaker condition. That is, as stated in Theorem 7 below, it is enough to show that
as
, for each
. In particular, in the examples of Feller processes mentioned above, this property is implied by continuity in probability.
Definition 1 generalizes to sub-Markovian transition functions, where it is not assumed that are probability measures. Instead, the inequality
imposed, so the probabilities could sum to less than one. As with general sub-Markovian transition functions, it is possible to extend the state space by adding a cemetery or coffin state
, and setting
. The open sets defining the topology on this space consists of the subsets
such that
is open in E. Equivalently,
is an isolated point and the subspace topology on E agrees with the original topology. Then,
is also an lccb space and defining
as before,
| (1) |
gives a Feller transition function on describing a process which can jump to the state
, and remain there.
The definition of Feller transition functions can be considered in the more general context of continuous linear semigroups on the Banach space . If
is a probability measure on E then its integral,
defines a linear map from
to
. The converse is given by the Riesz representation theorem, which I state here without proof.
Theorem 2 (Riesz-Markov) Let E be a locally compact Hausdorff space and
be a continuous linear functional. Then, there is a unique regular (finite signed) measure
on E such that
. Furthermore,
.
The condition that is regular is not important here, as all finite signed measures on the Borel sigma-algebra are regular in the case of lccb spaces. Then
is a probability measure if and only if L is positive and
. Similarly, a positive linear function
uniquely defines a transition kernel N such that
. The property that
, so that N is a transition probability is a bit trickier to state in terms of L. However, the inequality
is equivalent to
, allowing us to define sub-Markovian transition functions. A sub-Markovian Feller transition function
uniquely defines a strongly continuous semigroup of positive linear operators
on
such that
, simply by setting
. Conversely, applying the Riesz representation theorem, every such semigroup arises in this way from a unique sub-Markovian Feller transition function.
The main property of Feller processes, which we concentrate on here, is that they always have cadlag modifications.
Theorem 3 Any Feller process has a cadlag modification.
The proof of this is given below. A consequence is that any Feller transition function can be realized on the space of cadlag functions from
to E. This is a big improvement over Theorem 5 of the previous post, which applied to arbitrary transition functions but did not impose any properties on the paths of the process.
Corollary 4 Let E be an lccb space and
be the space of cadlag functions from
to E. Denote its coordinate process by
, let
be the sigma-algebra on
generated by
and, for each
, let
be the sigma-algebra generated by
.
Then, for any Feller transition function
and probability measure
on E, there is a unique probability measure on
with respect to which X is a Feller process with the given transition function and with initial distribution
.
Proof: By Lemma 3 of the previous post the measure , if it exists, is unique. We just need to construct one such measure.
Let with coordinate process
generating the sigma algebra
so that, by Theorem 5 of the previous post, there is a probability measure
on
with respect to which
is Markov with the given transition function and initial distribution. Then, by Theorem 3,
has a cadlag modification Y, say. As Y is cadlag, it defines a map
. Let
be the measure induced on
by this map. So X has the same distribution under
as Y does under
, and hence is Markov with the given transition function and initial distribution. ⬜
We now move on to the proof that Feller processes have cadlag versions. This will be split up into a couple of lemmas, the idea being to show that certain functions of Feller processes are supermartingales and, hence, existence of cadlag modifications for supermartingales can be applied.
For each , the resolvent
of a transition function
on a measurable space
is the kernel defined by
| (2) |
for each bounded measurable . For this to be well-defined, it is only necessary that
is measurable, which is true for Feller processes (since it is continuous for
). If
and the transition function
is Feller then, using dominated convergence inside the integral in (2),
for any sequence
and
for
tending to the point at infinity. So,
.
The resolvent identity
for follows directly from applying the definition (2) and applying a change of variables. Alternatively, applying the substitution
to (2) gives
| (3) |
In particular, for a Feller transition function, dominated convergence shows that as
for any
. Also, equation (3) implies that
is a transition probability.
The resolvent helps us find functions of the process which are supermartingales.
Lemma 5 Let X be a Markov process taking values in E and with transition function
. Then, for any nonnegative, bounded and measurable
and
,
is a supermartingale.
Proof: Expression (2) for the resolvent gives
| (4) |
So, if X is Markov with the given transition function and f is nonnegative then,
Applying this to the conditional expectation of M,
⬜
Next, it can be shown that if has a cadlag modification for enough functions
, then X itself must have a cadlag modification. This does, however, require the state space to be compact. Although Feller processes are defined above for arbitrary lccb spaces, it is always possible to reduce it to the case where E is compact. This can be done by taking the one-point compactification
of E. Then,
(for bounded measurable ) defines a Feller transition function on
which reduces to
on E. This describes a process which is either in E behaving according to the transition function
, or is fixed at the point at infinity.
Lemma 6 Let
be a compact topological space and
be a countable sequence of functions separating points in E.
Then, a stochastic process X taking values in E has a cadlag modification if
has a cadlag modification for all
.
Proof: We first show that a sequence in E is convergent if and only if
converges for every
, and that
is the unique element of E such that
for all
. By continuity, this is a necessary condition for convergence and for x to be the limit, so we only need to show that it is sufficient. By compactness, every sequence has at least one limit point, and a sequence converges if and only if the limit point is unique. So, suppose that
converges for all
and let
be limit points of
. Then,
and, as S separates points,
as required. Next, if x is any point satisfying
for
then,
. Since S separates points, we have
as promised.
Now suppose that has a cadlag modification
, say, for each k. Then, restricting to a set of probability one,
for all
and
. It follows that
, restricted to
, is right-continuous and has left and right limits at all nonnegative reals. By the condition above for convergence in E,
is also right-continuous with left and right limits everywhere in
. So, we can define the cadlag modification
⬜
Using Lemma 5 to find functions such that
has a cadlag modification and applying Lemma 6 to find a cadlag version gives us the proof of Theorem 3.
Proof of Theorem 3: We first prove this in the case where E is compact. Then, for each nonnegative , the process
is a supermartingale and, if it is right-continuous in probability, it will have a cadlag modification. In fact,
is right-continuous in probability for any
. This follows from the criterion that a sequence
of real-valued random variables converges to a limit Y in probability if and only if
for each continuous and bounded
and Y-measurable set S. If
and S is
-measurable then,
and in probability.
As E is an lccb space, there exists a countable set of nonnegative functions separating the points in E. Then,
has a cadlag modification and, since
as
, the countable set
also separates the points of E. By Lemma 6, X has a cadlag modification.
Finally, let us consider the case where E is not compact. Then, letting be its one-point compactification, X can also be considered as a Feller process with state space
. So, we may pass to a cadlag modification taking values in
, and it only needs to be shown that
and
for all t, with probability one. To prove this, choose a strictly positive
and
, and consider the submartingale
. The function
will be strictly positive on E, and can be extended to all of
by setting
. Letting
be the first time at which
, we can use optional sampling to get
for each and
. Letting n increase to infinity,
As with probability one,
is strictly positive and, therefore,
. As this holds for each t,
almost surely, meaning that
is almost surely positive for all T and, hence,
and
for all t.
We now show that it, in the definition of Feller processes, it is not necessary to impose the condition that is continuous under the norm topology, for
. In fact, the much weaker condition that
as
is enough.
Theorem 7 A transition function
on an lccb space E is Feller if and only if, for all
,
for all
.
as
, for each
.
Proof: That these properties are necessary is trivial, so we just prove that they are also sufficient. To show that is norm-continuous, it suffices to prove continuity at 0. In that case, if
then,
as required. Now, letting A be the set of all such that
as
, the idea is to show that every element of
is in A. In fact, A is closed under the norm topology. If
converge uniformly to a limit f then,
As , the right hand side tends to
which, by choosing n large, can be made as small as we like. So,
tends to 0, and
.
To find a sequence in A converging to any given , we make use of the resolvent. If
then, by (4),
As and
are transition probabilities, this gives
and
.
as . So,
. It only remains to show that
can be expressed as the uniform limit of such elements of {\t A}.
Choosing a sequence , consider
. By assumption,
as
, for all
. Then, applying dominated convergence in the integral in (3) gives
. This is not quite enough, as we need to find a senquence converging uniformly to
. However, Lemma 8 below states that it is possible to improve pointwise convergence to norm convergence just by passing to convex combinations. So, there is a sequence in A converging uniformly to
, which must therefore also be in A, as required. ⬜
Finally, the proof of Theorem 7 required the following lemma, which allows us to strengthen the convergence of a series in from pointwise to uniform convergence simply by passing to convex combinations. The proof of this is rather non-constructive, relying on the Hahn-Banach theorem for locally convex spaces and the Riesz representation theorem (Theorem 2) to give a proof by contradiction. The notation
denotes the set of finite linear combinations of elements of a set S.
Lemma 8 Let E be a locally compact space and
be a uniformly bounded sequence of functions in
converging pointwise to the limit
. That is,
for each
.
Then, there is a sequence
converging uniformly to
.
Proof: The result is equivalent to the statement that is in the norm closure S, say, of
. Suppose that this was not the case. Then, by the Hahn-Banach theorem, there exists a linear and norm-continuous map
such that
for some constant K and all
. Then, the Riesz representation theorem gives a finite signed measure
satisfying
for
. However, using bounded convergence, this leads to the following contradiction,
⬜
Mik – I moved your comment to the About page, and responded there, as it was not relevant to this post.
Dear George, thank you for this great post!
Do you think that it might be possible to include examples of processes that are almost Feller – and see how the properties that you prove in this series of posts break for these almost-feller processes ?
Best
Alekk
ps: any reference except Revuz-Yor and Rogers-Williams ?
Good idea! I’ll give some thought towards writing a post on “almost” Feller to show how the properties proven here can fail (i.e., existence of cadlag versions, the strong Markov property, right-continuity of the filtration and quasi-left-continuity).
The next post is going to be on Bessel processes, which *are* Feller. After that, I am planning on a post demonstrating a simple SDE whose solutions are local martingales but fail to be proper martingales. Coincidentally, they also just fail to be Feller processes but, as they satisfy all the properties I have proven for Feller properties, it doesn’t really give the kind of counterexample you are asking for.
Almost-Feller processes could fit into any of the following categories.
1) Ptf(x) is jointly continuous in t and x but not in C0(E) for f ∈ C0(E).
2) The definition of Feller process is satisfied with Cb(E) in place of C0(E). The is, Ptf is continuous for bounded continuous f, and t → Ptf is continuous under the uniform norm.
3) t → Ptf is uniformly continuous for f ∈ C0(E), but Ptf(x) is not continuous in x.
4) E is not lccb. Either because is not locally compact or because it does not have a countable base.
Examples satisfying (1) and not having cadlag modifications are easy to construct. Just take something standard like Brownian motion or reflecting Brownian motion and remove the point {0} from the state space. Seems like a bit f a cheat, but I think all examples are like this. They are Feller processes in a larger state space with some points removed.
I think processes in class (2) satisfy all the properties of Feller processes anyway. You can pass to a larger space on which it is Feller (using the Gelfand representation) and then show that it doesn’t hit the additional points in the state space anyway (I think…).
Processes in class (3) are easily constructed which fail the strong Markov property. E.g., consider a real-valued process which either stays at zero or is a Brownian motion. This has transition function
but fails the strong Markov property at times T with XT=0. Again, I think all examples are similar to this in that they can be considered as processes on a larger space, but with some points identified. You can also construct examples in a similar way in which the completed filtration is not right-continuous.
I need to think about (4).
Any nice examples you or anyone else know of would be gratefully accepted!
For references, I’m not sure what is best. I am mainly working through the subject from the perspective of semimartingales in these notes, rather than getting deeply into Markov process theory. All the results I cover here are included in Revuz-Yor. Checking Kallenberg, Foundations of Modern Probability, I see that it has a chapter on Feller Processes and Semigroups.
Hi George,
I was curious about what are necessary conditions that can ensure that the transform by a fonction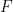 of a Markov (or Feller) Processes ensures that it stays Markov (or Feller).
of a Markov (or Feller) Processes ensures that it stays Markov (or Feller).
In particular, for a Markov (or Feller) process defined by an SDE (with coefficients s.t. we have existence and uniqueness), is there necessary conditions that would lead to an explicit calculation (using the coefficients of the SDE or the infinitesimal generator of the process itself and of its transform by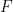 ).
).
The question comes from the fact that I know a few sufficient conditions, but when those are not fullfiled, I feel it is always a case by case study that determines if yes or no the transformed process is Markovian (or Feller), and no general methodology is applicable.
As asked the question is not really completley “well posed” but an answer with additional assumptions on the process itself would still be interesting.
Best regards
Sorry for not responding quicker to this question. I did see it, but didn’t have a good answer immediately. I don’t think that there is a good answer to this though. You can easily construct necessary conditions and sufficent conditions on F, but I don’t think there are any useful conditions which are both necessary and sufficient. So, it does depend on your particular application and I think you are right that requires a case by case study.
Hi George,
Thank’s for your answer indeed the problem seems quite difficult to tackle. But I wonder if it is not linked in some way to Lie Group classification of SDE ( you can take a look at Kozlov article and the references therein : “The Group Classification of a Scalar Stochastic Differential Equation” -JOURNAL OF PHYSICS A: MATHEMATICAL AND THEORETICAL,J. Phys. A: Math. Theor. 43 (2010) 055202 (13pp)).
In particular if the group of transformation preserves the Markov property ( I’m not sure about this) and if it can be showed that only those transforms can do so ( even less sure about this), then there’s might be some hope.
Best regards
Hi there, I really like your blog!
I am an econometrician myself, and I appreciate your blog for the intuition that is not provided by many text books. I am actually writing a paper about optimal stopping in higher dimensions, where I actually use Feller processes. But I’m not an expert. I was hoping perhaps you could help me find a reference for a question, that I believe is possibly relatively simple, but haven’t been able to prove it / find a reference. Any suggestions are greatly appreciated.
If we have a Feller process with an infinitesimal generator and resolvent
and resolvent 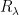 , then we have
, then we have  uniformly as
uniformly as 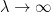 for any
for any 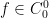 . We also have the ‘inverse property’ of the resolvent
. We also have the ‘inverse property’ of the resolvent  for any
for any 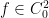 . Multiplying by
. Multiplying by  and re-writing this equality, we obtain
and re-writing this equality, we obtain  . This shows that
. This shows that 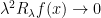 for some
for some  as
as 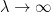 if and only if
if and only if 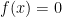 and
and  . This property clearly holds for any
. This property clearly holds for any  if
if  is
is 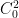 .
.
But now suppose is only
is only 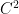 locally in the neighbourhoud of the point
locally in the neighbourhoud of the point  , where we evaluate the limit
, where we evaluate the limit  , but elsewhere it is only
, but elsewhere it is only 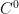 . Specifically, in my case, it has a kink on a hyper surface of measure zero. But we evaluate
. Specifically, in my case, it has a kink on a hyper surface of measure zero. But we evaluate  away from this hyper surface, i.e. we evaluate the limit where
away from this hyper surface, i.e. we evaluate the limit where 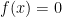 and
and  . Does the result
. Does the result 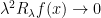 remain true? I believe it does, perhaps by Dynkin’s formula, since
remain true? I believe it does, perhaps by Dynkin’s formula, since  is
is 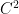 in any ball around
in any ball around  . Any ideas to the truth of the statement and/or possible references?
. Any ideas to the truth of the statement and/or possible references?
Many thanks & best wishes!
PS Perhaps the last sentence of my second paragraph is a bit unclear. I meant to say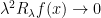 if and only if
if and only if 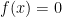 as well as
as well as  are true at the specific location
are true at the specific location  (and in its infinitesimal neighbourhood for the derivatives to make sense) where we evaluate the limit. Does this statement remain true if
(and in its infinitesimal neighbourhood for the derivatives to make sense) where we evaluate the limit. Does this statement remain true if 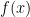 is only locally
is only locally 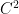 , i.e. in a small ball around the location
, i.e. in a small ball around the location  , where
, where  is identically zero in this ball, such that
is identically zero in this ball, such that 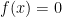 and
and  ? (I believe so, but can only find proofs if
? (I believe so, but can only find proofs if  is globally
is globally 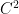 and vanishes at infinity, i.e. if
and vanishes at infinity, i.e. if  is
is 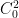 , which doesn’t hold for me.)
, which doesn’t hold for me.)
Hi. I’m not sure where you would find a precise statement of what you are asking. However, I do have a couple of comments. First, you are using where I think you need to be using the domain of A. So, I suppose that you are only considering generators with
where I think you need to be using the domain of A. So, I suppose that you are only considering generators with 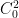 in their domain. Such generators can be expressed as a continuous diffusion term plus a jump term (Revuz & Yor state this in their book, Continuous Martingales and Brownian motion). Your later comment suggests that you are only considering the continuous case (i.e., where you say that Af(x)=0 if f is 0 in a neighbourhood of x). Either way, if f is only
in their domain. Such generators can be expressed as a continuous diffusion term plus a jump term (Revuz & Yor state this in their book, Continuous Martingales and Brownian motion). Your later comment suggests that you are only considering the continuous case (i.e., where you say that Af(x)=0 if f is 0 in a neighbourhood of x). Either way, if f is only 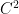 in a neighbourhood of x, then Af is strictly speaking not well defined as f is not in the domain of A. However, you can define Af in the
in a neighbourhood of x, then Af is strictly speaking not well defined as f is not in the domain of A. However, you can define Af in the 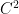 region as the non-
region as the non-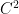 points will only contribute to the jump component, which does not require smoothness properties. As you say, it then reduces to the case where f is 0 in the neighbourhood of x. I think you just need to show that, in that case,
points will only contribute to the jump component, which does not require smoothness properties. As you say, it then reduces to the case where f is 0 in the neighbourhood of x. I think you just need to show that, in that case,  . This certainly looks like it should be true. Or, prove directly that
. This certainly looks like it should be true. Or, prove directly that 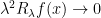 which, I think, follows from
which, I think, follows from  .
.
Btw, I moved your comment to the relevant post.
If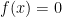 and
and  is well defined, you can use.
is well defined, you can use.
Many thanks! I am indeed considering Feller diffusions processes, i.e. no jump component, for which the domain of includes (at least) the space of
includes (at least) the space of 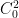 functions (indeed as in Revuz and Yor). I should have said for some function
functions (indeed as in Revuz and Yor). I should have said for some function  in the domain of
in the domain of  , so I was sloppy. Yes I agree that
, so I was sloppy. Yes I agree that 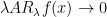 looks like it should be true if
looks like it should be true if 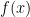 is locally identically zero, i.e. in some ball around
is locally identically zero, i.e. in some ball around  of strictly positive radius. To me, it seems irrelevant what happens outside of the ball as long as
of strictly positive radius. To me, it seems irrelevant what happens outside of the ball as long as  remains continuous and bounded everywhere (we could still say the resolvent maps
remains continuous and bounded everywhere (we could still say the resolvent maps  to itself, right?). Thanks for the derivation as well (last line should probably have
to itself, right?). Thanks for the derivation as well (last line should probably have  rather than
rather than 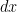 ?) I will let you know when our paper is ready and mention you in the acknowledgements. If you would be interested in reading the draft, then let me know. It’s about a new (we believe) class of monotone and uniformly converging algorithms for calculating the value function for optimal stopping problems in higher dimensions, which are considered hard because they feature free boundaries, using (global) resolvent/integral methods rather than (local) PDE/finite difference methods. Best wishes, Rutger-Jan
?) I will let you know when our paper is ready and mention you in the acknowledgements. If you would be interested in reading the draft, then let me know. It’s about a new (we believe) class of monotone and uniformly converging algorithms for calculating the value function for optimal stopping problems in higher dimensions, which are considered hard because they feature free boundaries, using (global) resolvent/integral methods rather than (local) PDE/finite difference methods. Best wishes, Rutger-Jan
I was convinced but now I’m having second thoughts… Again take and assume
and assume 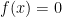 for all
for all  inside some ball
inside some ball  of radius
of radius  centred at some location
centred at some location  . Clearly,
. Clearly,  for any
for any 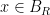 . The question remains whether this implies
. The question remains whether this implies  \to 0](https://s0.wp.com/latex.php?latex=A+%5B%5Clambda+%28R_%5Clambda+f%29%5D%28%5Cbar%7Bx%7D%29+%5Cto+0&bg=ffffff&fg=000000&s=0&c=20201002) . While this seems plausible, it is not obvious that the derivatives converge to zero… At least, it is not *generally* true that the derivative converges to zero if the value converges to zero.
. While this seems plausible, it is not obvious that the derivatives converge to zero… At least, it is not *generally* true that the derivative converges to zero if the value converges to zero.
It is true in the context you ask for. I can provide more details later.
That is all I need, so that would be great!! Curious what your solution is. I intuitively believe it to be true, but that’s not good enough, so many thanks for your help.
Consider the following statements.
i) If exists for some
exists for some  And
And  then
then  as
as  .
. is zero in a neighbourhood of
is zero in a neighbourhood of  then
then  .
.
ii) If
Combining these gives what you want. For the first, use
For the second, choose with
with  And
And  in a neighbourhood of
in a neighbourhood of  . Then,
. Then,  so,
so,
So I was on travels, but that’s great, thanks! In (ii) you wrote and
and  , was that intentional? Can we take both in
, was that intentional? Can we take both in  ? To make things easier, suppose
? To make things easier, suppose  is actually non-negative, so we can take
is actually non-negative, so we can take  , with
, with  and
and 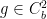 and both
and both  and
and 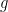 equal to zero in the neighbourhood of
equal to zero in the neighbourhood of  . Then using your argument we can write
. Then using your argument we can write 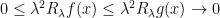 , since
, since 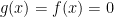 in the vicinity of
in the vicinity of  , and we can use all the nice resolvent properties on
, and we can use all the nice resolvent properties on  , right?
, right?
I think I may have got a bit mixed up with the indices there — was intended to be bounded, measurable, and vanishing at infinity.
was intended to be bounded, measurable, and vanishing at infinity. 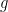 is twice continuously differentiable and vanishing at infinity. The argument should generalise to arbitrary bounded measurable
is twice continuously differentiable and vanishing at infinity. The argument should generalise to arbitrary bounded measurable  though, with a bit more work.
though, with a bit more work.
Dear George, is a Hawkes process a Feller process?
In Theorem 2 (and Lemma 8), I think you need to assume additionally that the space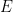 is
is  -compact to be able to conclude that the measure
-compact to be able to conclude that the measure 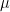 is finite. The measure
is finite. The measure 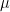 is in general only locally finite.
is in general only locally finite.
Thank you for your amazing blog.
Nevermind, the finiteness is indeed guaranteed by the continuity.