In the previous post, the concept of Feller processes was introduced. These are Markov processes whose transition function satisfies certain continuity conditions. Many of the standard processes we study satisfy the Feller property, such as standard Brownian motion, Poisson processes, Bessel processes and Lévy processes as well as solutions to many stochastic differential equations. It was shown that all Feller processes admit a cadlag modification. In this post I state and prove some of the other useful properties satisfied by such processes, including the strong Markov property, quasi-left-continuity and right-continuity of the filtration. I also describe the basic properties of the infinitesimal generators. The results in this post are all fairly standard and can be found, for example, in Revuz and Yor (Continuous Martingales and Brownian Motion).
As always, we work with respect to a filtered probability space . Throughout this post we consider Feller processes X and transition functions
defined on the lccb (locally compact with a countable base) space E which, taken together with its Borel sigma-algebra, defines a measurable space
.
Recall that the law of a homogeneous Markov process X is described by a transition function on some measurable space
. This specifies that the distribution of
conditional on the history up until an earlier time
is given by the measure
. Equivalently,
for any bounded and measurable function . The strong Markov property generalizes this idea to arbitrary stopping times.
Definition 1 Let X be an adapted process and
be a transition function.
Then, X satisfies the strong Markov property if, for each stopping time
, conditioned on
the process
is Markov with the given transition function and with respect to the filtration
.
As we see in a moment, Feller processes satisfy the strong Markov property. First, as an example, consider a standard Brownian motion B, and let be the first time at which it hits a fixed level
. The reflection principle states that the process
defined to be equal to B up until time
and reflected about K afterwards, is also a standard Brownian motion. More precisely,
is a Brownian motion. This useful idea can be used to determine the distribution of the maximum . If
then either the process itself ends up above K or it hits K and then drops below this level by time t, in which case
. So, by the reflection principle,
In fact, the reflection principle is a consequence of the strong Markov property, as follows. First, by the strong Markov property, the process is a Brownian motion independently of the stopped process
. As the law of standard Brownian motion is symmetric, this has the same distribution as
. So,
has the same joint distribution as
.
Let us now write out explicitly what the strong Markov property means. If is a stopping time then, conditioning on
, the Markov property applied to
under the filtration
is equivalent to
| (1) |
(almost surely) for all times . Simplifying this a bit gives the following.
Lemma 2 A process X is strong Markov with transition function
on state space E if and only if, for every finite stopping time
, every
, and bounded measurable
,
(2)
Proof: Applying (1) with s=0 gives (2). To prove the converse, suppose that (2) holds and pick any stopping time and times
. Then,
is a finite stopping time for any constant
and, by (2),
Then, using the fact that and
agree on the set
,
Letting T increase to infinity gives (1). ⬜
We now prove that Feller processes are strong Markov.
Theorem 3 Every cadlag Feller process satisfies the strong Markov property.
Proof: Suppose that X is a cadlag Feller process with transition function . We just need to show that (2) holds for a bounded stopping time
and fixed time
. First, the case where
takes values in a countable set
is easily handled, and does not even require the Feller property. Just the Markov property is needed. Letting Z be a bounded
-measurable random variable,
is
-measurable for all fixed times s, giving
Next let be any stopping time and, for each nonnegative integer n, let
be the first time after
which is a multiple of 1/n. That is
, which is a stopping time taking values in a countable subset of
. So,
for bounded -measurable Z. From the definition of the Feller property, if
then
is jointly continuous in t and right-continuous in s. So, taking limits
This extends to all bounded measurable by the functional monotone class theorem, giving (2) as required. ⬜
In the study of continuous-time stochastic processes it is common to assume that the underlying filtration satisfies the `usual conditions’. That is, it is complete and right-continuous. On the other hand, in these notes, I have not done this. Completeness of the filtration has been used throughout, so that the debut theorem for right-continuous processes holds and so that we can take cadlag versions of processes. However, I have not been assuming right-continuity of the filtration. For Feller processes, as it turns out, right-continuity is automatic in any case. That is, the complete filtration generated by a Feller process is right-continuous.
Theorem 4 Let X be a Feller process and
be its natural filtration. Suppose that
is the sigma algebra generated by
together with the zero probability sets in
.
Then,
is a right-continuous filtration,
Proof: Suppose that X is Feller with state space E and transition function . The aim is to prove the identity
| (3) |
(almost surely) for every bounded -measurable random variable Z. As
is the sigma-algebra generated by
(up to zero probability sets), it is enough to prove the result for Z of the form
| (4) |
for times and functions
. The functional monotone class theorem then extends this to all bounded and
-measurable Z.
First, consider for some time
and
. As the Feller process X has a cadlag modification,
will be right-continuous in probability w.r.t. t. So, the Markov property gives
as required.
Extending the result to all Z of the form (4) is just an application of induction on n. So, suppose that the (3) holds for n replaced by n-1. If then Z is
-measurable, and the result is trivial. If
then setting
gives
Finally, if then setting
and
the Markov property gives . Also, the induction hypothesis gives (3) with
in place of Z. So,
as required. ⬜
One consequence of the right-continuity of the filtration is the following zero-one law. Consider, for example, a standard Brownian motion B. It can be shown hits zero infinitely often for t in any neighborhood of 0, with probability one. Events such as this are
-measurable for each
and, therefore,
measurable. The following result states that all such events have probability zero or one. So, in fact, any Feller process with fixed initial state
must either equal x infinitely often in any neighbourhood of 0 with probability one or, again with probability one, there must be a nonempty interval
on which it does not equal x.
Corollary 5 (Blumenthal’s zero-one law) Let X be a Feller process with fixed initial value
. Letting
be its natural filtration, every
satisfies
or
.
Proof: As is fixed at x, the sigma-algebra
it generates contains only sets with probability zero or one. If
is the sigma-algebra generated by
together with the zero probability sets then, by Theorem 4,
. However,
is generated by sets of zero probability. ⬜
Recall that, for a Poisson process X, its jump times are totally inaccessible. That is, for any predictable stopping time , it is almost surely continuous at time
, so
. This property holds for all Feller processes, and is referred to as quasi-left-continuity. By definition, a stopping time
is predictable if there exists a sequence
of stopping times increasing to
. Then,
as
. For arbitrary jointly measurable processes, quasi-left-continuity is defined as follows.
Definition 6 A process X taking values in a topological space E is quasi-left-continuous if and only if, for each finite stopping time
and sequence of stopping times
increasing to
,
almost surely as
.
We now prove that Feller processes satisfy this property.
Theorem 7 Every cadlag Feller process is quasi-left-continuous.
Proof: Let X be a cadlag Feller process on state space E and with transition function . Then choose a finite predictable stopping time
and a sequence of stopping times
increasing to
. The aim is to prove the identity
| (5) |
for bounded measurable functions . Then, taking
gives
as required.
As the Borel sigma-algebra on an lccb space E is generated by functions in , it is sufficient to prove (5) for
for functions
, as the functional monotone class theorem then extends (5) to all bounded and measurable u. Given any such functions f, g, the continuity of
in both x and t together with the strong Markov property (2) applied at the stopping times
gives,
for any . Taking the limit as
gives
as required. ⬜
Another property of homogeneous Poisson processes is that the times between jumps are exponentially distributed. This also carries through to arbitrary Feller processes in the following form; the time spent at any fixed level x, if it is not zero or infinite, has the exponential distribution. In fact, the following result almost holds for all right-continuous Markov processes. The Feller property is only used to show that is a stopping time (using right-continuity of the filtration) and that X is discontinuous at
whenever
(using the strong Markov property).
Theorem 8 Let X be a cadlag Feller process with fixed initial value
, and set
If the underlying filtration is complete then
is a stopping time. Furthermore, one of the following properties holds.
almost surely.
almost surely.
- There is a
such that
has the
distribution. In this case,
with probability one, so X is discontinuous at
.
Proof: Without loss of generality we can assume that the underlying filtration is the one generated by X together with the zero probability sets, since the filtration can always be replaced by this without altering the conclusion of the theorem. By right-continuity of X,
Theorem 4 says that the filtration is right continuous and, by the following, is a stopping time.
Now define the function by
. For any
, conditioning on the set
gives
and, by the Markov property, the process
has the same distribution as
. Therefore,
conditioned on
has the same distribution as
,
The only solutions to this functional equation for a right-continuous and decreasing function are,
-
, in which case
almost surely.
-
, in which case
almost surely.
-
for some constant
. So,
has the exponential distribution of rate
. Now define the process
. By definition of
,
is almost surely zero. However, by the strong Markov property, conditioned on the event
the random variable
has the same distribution as
and is therefore almost surely positive. So,
⬜
Infinitesimal Generators
Except in certain simple cases it is often not possible to explicitly write out the transition function describing a Feller process. Instead, the infinitesimal generator is used. This approximately describes the transition kernel for small times t, and can be viewed as the derivative of
at time 0,
. As the transition function is likely not to be differentiable in any strong sense, the generator is only defined on some subset of
.
Definition 9 Let
be a Feller transition function on the lccb space E. Then,
is said to be in the domain
of the infinitesimal generator if the limit
(6) exists under the uniform topology on
.
The operator
is called the infinitesimal generator of the semigroup
.
Equation (6) can alternatively be written as
| (7) |
where denotes a term vanishing faster than t as
. So, the generator A gives the first-order approximation to
for small t.
Restricted to , the operator
is differentiable with derivative given by
. Equation (8) is a version of the Kolmogorov backward equation.
Theorem 10 Let
. Then,
for all
. Furthermore,
is differentiable (w.r.t. the norm topology on
) and
(8)
Proof: By definition, tends to
in
as
, over
. Applying the bounded linear operator
to this gives
as over
. This shows that
has the right-hand derivative
. We need to extend this to show that it is actually differentiable. By the Feller property,
is continuous in s. In fact, all functions with a continuous right-hand derivative are differentiable. We can integrate to get
as . Therefore,
is indeed differentiable. Next,
as , over
. By definition this means that
and
. ⬜
Recall from the previous post that, associated with the transition function , there is a resolvent
defined for any
as
This is a transition kernel on E and, if is Feller, then
for all
. Restricted to
,
is a continuous linear map satisfying
and
as
. Resolvents and infinitesimal generators are closely related.
Theorem 11 Let
be a Feller transition function and
. Then,
is equal to the image of the resolvent
on
and, considering
as a map from
to
,
(9)
Proof: The second of equations (9) is just a rearrangement of the first. We can apply to
for any
and
,
By the Feller property, as
, giving
So, by equation (7), and
. Rearranging gives
| (10) |
Now, choosing any , equation (8) and integration by parts gives,
Rearranging gives , so
. Together with (10), this gives equation (9) as required. ⬜
Using the resolvent simplifies the proofs of some of the properties of the generator. In particular, its domain is dense in and A is closed. In the following lemma, the topology given by the uniform norm on
is used.
Lemma 12 The domain
is a dense subset of
, and A is a closed operator. That is, if
converge to
such that
, then
and
.
Proof: Setting , Theorem 11 gives
. Taking the limit
then, as
is a bounded operator, this gives
. Again by Theorem 11, this says that f is in
and
. ⬜
A Feller transition function is uniquely determined by its generator. However, this result not nearly as useful as it sounds. This is because, in all but a small number of special cases, we do not know what the domain is. Usually, we just have A defined on some dense subspace of
, such as the twice continuously differentiable functions, and this is not enough to apply the following result.
Lemma 13 Let
and
be Feller transition functions on an lccb space E with generators A and B respectively.
Suppose that the domains of the generators satisfy
and, restricted to
,
. Then,
for all t.
Proof: Denote the resolvents of and
by
and
respectively. Theorem 11 gives
for all . So, the resolvents are identical. However, resolvents are just Laplace transforms of the transition function and, by invertibility of Laplace transforms,
for almost every t. By continuity in t,
as required. ⬜
An alternative proof of Lemma 13 follows from applying (8) for any ,
So, .
Finally, the generator of a Feller process can be rewritten in terms of a martingale problem. The martingale approach, introduced by Stroock and Varadhan, is a very useful method in the theory of stochastic differential equations and Markov processes. For example, it is instrumental in the famous Stroock-Varadhan uniqueness theorem which shows that stochastic differential equations of the form
satisfy uniqueness in law for the n-dimensional process X. This is under the condition that are continuous functions such that
is a nonsingular nxn matrix for any x, and
are bounded and measurable.
The martingale description of the generator is as follows.
Lemma 14 Let X be a cadlag Feller process with transition function
and generator A. Then, for
, the process
is a martingale.
Proof: Choose times and let Z be a bounded
-measurable random variable. Taking expectations of
and applying the Markov property gives,
as required. Here, (8) has been used to express as a derivative. ⬜
Lemma 14 almost gives a complete description of the generator associated with a Feller process X, but not quite. To strengthen this result to give an alternative characterization of the generator, we must consider running the Markov process X from each possible starting position .
In the following theorem, we let be the set of cadlag functions
with coordinate process
. Then,
is the sigma-algebra generated by
and
. For each
, Corollary 4 of the previous post implies that there is a unique probability measure
on
under which X is a Feller process with the given transition function and
. Then,
is a filtered probability space.
Theorem 15 Let
be a Feller transition function and
. Then,
and
if and only the process
is a martingale under the measure
for all
.
Proof: If then Lemma 14 says that M is a martingale. Conversely, suppose that M is a martingale under the measure
. Then,
However, the Feller property says that as
, giving
By equation (7), this says that and
. ⬜
For example, suppose that is an n-dimensional process satisfying the stochastic differential equation
for an m-dimensional Brownian motion B and measurable functions . Defining the function
by
, consider the differential operator
For any twice-continuously differentiable function , Ito’s lemma gives
So, is a local martingale. If it is known that solutions to the SDE are in fact Feller processes, such as is the case when the coefficients are Lipschitz continuous, then Theorem 15 says that any twice continuously differentiable
such that
vanishes at infinity is in the domain of the generator, and the generator agrees with L on such functions.
Hey George,
just stumbled upon your blog, very cool stuff! I’d like to read a bit more on SDEs permitting a solution which is a Feller process. This can become very nasty I think, so I am interested in some (hopefully) easy to check criteria. I have seen that even simple SDEs, driven by Levy Processes are not Feller. There is a counterexample in the phd thesis of Schnurr (check apendix B): http://deposit.ddb.de/cgi-bin/dokserv?idn=995080879&dok_var=d1&dok_ext=pdf&filename=995080879.pdf
I have some Levy driving process, so not sure if the solution is Feller (which would be nice). Any references? Thanks.
Hi.
I don’t have any references to hand (but do remember that there are theorems giving sufficient conditions for a solution to an SDE to be Feller). You need to check several conditions (i) Uniquess in law (ii) Weak existence of solutions (iii) Continuity with respect to initial conditions (iv) Time homogenity and (v)![E_x[f(X_t)]\to0](https://s0.wp.com/latex.php?latex=E_x%5Bf%28X_t%29%5D%5Cto0&bg=ffffff&fg=000000&s=0&c=20201002) as
as 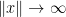 for bounded functions f of compact support.
for bounded functions f of compact support.
Conditions (i) and (ii) are things that you need to check in any case. Also, (iii) is the kind of result that would normally be proven along with uniqueness in law, and will hold for continuous coefficients. Property (iv) should be clear when it holds, and holds for an SDE with no time dependence in the coefficients and driven by independent Lévy processes. Properties (i)-(iii) will be satisfied for locally Lipschitz coefficents as long as the solution doesn’t blow up. So, (v) can be the tricky one. You need to show that the probability of being within some compact region at a fixed time t vanishes as the initial state goes to infinity. Thinking about it, if you have an SDE
for a Lévy process Z = (Z1,…,Zn) then I think that (v) will be satisfied as long as ak has sub-linear growth. This is because the size of jump in Z required for X to jump back to near the origin grows to infinity as X becomes large. The counterexample you mention, (B.3) in the linked paper, has ak growing linearly in X. For continuous driving terms (Brownian motion + drift) linear growth is enough for (v) to be satisfied.
I don’t have time to be looking for references now, but, if I come across any references I’ll post here.
Very nice blog indeed.
Something I have been wondering about for a while is under which conditions a Feller process that is strongly Markov would also have a reflection principle. More generally speaking, under which conditions would a (multi-dimensional) process that is strongly Markov also posses a reflection principle? I haven´t come across any references that treats this problem.
Hello,
I have a question that I would like to ask you. If we have a property A for Feller processes with negative jumps then we can say that the property A holds for Levy processes with negative jumps, right?
Is this true? Feller processes contain Levy processes?
I hope to receive your answer soon!
Thank you!
Yes, all Levy processes are Feller.
Dear Mr.George Lowther,
Thank you for such a nice blog. I would like to know if a doubly stochastic Poisson process (i.e. with stochastic intensity) satisfies Theorem 4 above, and if not then eventually under which condition it would be true (e.g. when the intensity process is a levy process?).
Looking forward to your reply.
I think you need to formulate it precisely, but I expect that a necessary (and maybe sufficient) condition is that the filtration generated by the intensity process is right-continuous.
Hi, I think there is a typo on the first line of the paragraph before Definition 6. should be
should be  .
.
Fixed. Thanks!
Hi, I think there is a typo in the proof of theorem 8, item 3, , should be
, should be  .
.
Fixed. Thanks!
Hi, I think there is a typo in the proof of lemma 14, second line of eqnarray, first term:![\displaystyle={\mathbb E}\left[Z(P_{t-s}f(X_t)-f(X_s))\right]](https://s0.wp.com/latex.php?latex=%5Cdisplaystyle%3D%7B%5Cmathbb+E%7D%5Cleft%5BZ%28P_%7Bt-s%7Df%28X_t%29-f%28X_s%29%29%5Cright%5D&bg=ffffff&fg=000000&s=0&c=20201002) should be
should be ![\displaystyle={\mathbb E}\left[Z(P_{t-s}f(X_s)-f(X_s))\right]](https://s0.wp.com/latex.php?latex=%5Cdisplaystyle%3D%7B%5Cmathbb+E%7D%5Cleft%5BZ%28P_%7Bt-s%7Df%28X_s%29-f%28X_s%29%29%5Cright%5D&bg=ffffff&fg=000000&s=0&c=20201002) .
.
Fixed. Thanks!
Hi George,
This is all really well explained, I get it better now. Which are the sources, particularly books, you used for Feller processes, including Hille Yosida Theorem? How about your SDE blogs? I’m trying to learn more deeply about these topics and always find good books really helpful.
Thanks and keep up the good work 🙂
Alex
Very Rich content and helpful!
I have one question about equation(4), is there any conclusion/reference here to state that the Z in (4) is the generator of the filtration? Maybe it is mentioned in your other blogs, but I miss it.
I found some similay result but only for Brownian motion in Exercise3.14 in Oksendal‘s SDE book.
Thank you!