Upcrossings, Downcrossings, and Martingale Convergence

George Lowther Filtrations and Processes, Stochastic Calculus Notes 6 December 0928 February 23

The number of times that a process passes upwards or downwards through an interval is refered to as the number of upcrossings and respectively the number of downcrossings of the process.

Consider a process ${X_t}$ whose time index ${t}$ runs through an index set ${\mathbb{T}\subseteq{\mathbb R}}$ . For real numbers ${a<b}$ , the number of upcrossings of ${X}$ across the interval ${[a,b]}$ is the supremum of the nonnegative integers ${n}$ such that there exists times ${s_k,t_k\in\mathbb{T}}$ satisfying

$\displaystyle s_1<t_1<s_2<t_2<\cdots<s_n<t_n$

(1)

and for which ${X_{s_k}\le a<b\le X_{t_k}}$ . The number of upcrossings is denoted by ${U[a,b]}$ , which is either a nonnegative integer or is infinite. Similarly, the number of downcrossings, denoted by ${D[a,b]}$ , is the supremum of the nonnegative integers ${n}$ such that there are times ${s_k,t_k\in\mathbb{T}}$ satisfying (1) and such that ${X_{s_k}\ge b>a\ge X_{t_k}}$ .

Note that between any two upcrossings there is a downcrossing and, similarly, between any two downcrossings there is an upcrossing. It follows that ${U[a,b]}$ and ${D[a,b]}$ can differ by at most 1, and they are either both finite or both infinite.

The significance of the upcrossings of a process to convergence results is due to the following criterion for convergence of a sequence.

Theorem 1 A sequence ${x_1,x_2,\ldots}$ converges to a limit in the extended real numbers if and only if the number of upcrossings ${U[a,b]}$ is finite for all ${a<b}$ .

Proof: Denoting the infimum limit and supremum limit by

$\displaystyle l = \liminf_{n\rightarrow\infty}x_n,\ u=\limsup_{n\rightarrow\infty}x_n,$

then ${l\le u}$ and the sequence converges to a limit if and only if ${l=u}$ .

First, suppose that the sequence converges. If ${l>a}$ then there is an ${N}$ such that ${x_n>a}$ for all ${n\ge N}$ . So, all upcrossings of ${[a,b]}$ must start before time ${N}$ , and we may conclude that ${U[a,b]\le N}$ is finite. On the other hand, if ${l\le a}$ then ${u=l<b}$ and we can infer that ${x_n<b}$ for all ${n\ge N}$ and some ${N}$ . Again, this gives ${U[a,b]\le N}$ .

Conversely, suppose that the sequence does not converge, so that ${u>l}$ . Then choose ${a<b}$ in the interval ${(l,u)}$ . For any integer ${n}$ , there is then an ${r>n}$ such that ${x_r>b}$ and an ${s>n}$ with ${x_s<a}$ . This allows us to define infinite sequences ${s_k,t_k}$ by ${t_0=0}$ and

$\displaystyle \setlength\arraycolsep{2pt} \begin{array}{rl} &\displaystyle s_k=\inf\left\{m\ge t_{k-1}\colon x_{m}\le a\right\},\smallskip\\ &\displaystyle t_k=\inf\left\{m\ge s_{k}\colon x_{m}\ge b\right\}, \end{array}$

for ${k\ge 1}$ . Clearly, ${s_1<t_1<s_2<\cdots}$ and ${x_{s_k}\le a<b\le x_{t_k}}$ for all ${k\ge 1}$ , so ${U[a,b]=\infty}$ . ⬜

This convergence criterion is particularly suited to applications in stochastic calculus and martingale theory because bounds for the number of upcrossings and downcrossings of a process can be obtained in terms of stochastic integrals.

In these stochastic calculus notes, I am mainly concerned with stochastic processes ${X_t}$ with time index ${t}$ running through the positive real numbers. However, for the purposes of this post, it is useful to consider arbitrary index sets ${\mathbb{T}\subseteq{\mathbb R}}$ . We work under a probability space ${(\Omega,\mathcal{F},{\mathbb P})}$ and a filtration of sigma-algebras ${\{\mathcal{F}_t\}_{t\in\mathbb{T}}}$ . Consider an elementary predictable process of the form ${\xi_t=\sum_{k=1}^nZ_k1_{\{s_k<t\le t_k\}}}$ for times ${s_k<t_k}$ in ${\mathbb{T}}$ and ${\mathcal{F}_{s_k}}$ -measurable random variables ${Z_k}$ . Its integral with respect to ${X}$ is given by

$\displaystyle \int\xi\,dX=\sum_{k=1}^nZ_k(X_{t_k}-X_{t_{k-1}}).$

In particular, this includes processes ${\xi_s(\omega)\equiv 1_{\{(t,\omega)\in A\}}}$ for elementary predictable sets ${A}$ of the form

$\displaystyle A=\bigcup_{k=1}^n (s_k,t_k]\times F_k$

(2)

for times ${s_k<t_k}$ in ${\mathbb{T}}$ and sets ${F_k\in\mathcal{F}_{s_k}}$ .

The number of upcrossings of an interval ${[a,b]}$ can be computed as follows.. Set ${t_0=0}$ and define ${s_1,s_2,\ldots}$ and ${t_1,t_2,\ldots}$ by

$\displaystyle \setlength\arraycolsep{2pt} \begin{array}{rl} &\displaystyle s_k=\inf\left\{t\in\mathbb{T}\colon t\ge t_{k-1}, X_t\le a\right\}\in\mathbb{T}\cup\{\infty\},\smallskip\\ &\displaystyle t_k=\inf\left\{t\in\mathbb{T}\colon t\ge s_k, X_t\ge b\right\}\in\mathbb{T}\cup\{\infty\}. \end{array}$

It is easily seen that ${X_{s_k}\le a<b\le X_{t_k}}$ whenever ${t_k<\infty}$ and, if ${X_{s}\le a<b\le X_{t}}$ for times ${s<t}$ in ${\mathbb{T}}$ , then ${s\le s_k<t_k\le t}$ for some ${k}$ . The number of upcrossings of ${[a,b]}$ is therefore equal to the maximum ${n}$ such that ${t_n<\infty}$ . So, ${U[a,b]=n}$ and, letting ${\xi_t}$ be the elementary process ${\sum_k 1_{\{s_k<t\le t_k\}}}$ gives the following inequality (see also, the figure above)

$\displaystyle \setlength\arraycolsep{2pt} \begin{array}{rcl} \displaystyle\int\xi\,dX &\displaystyle= &\displaystyle \sum_{k=1}^\infty (X_{t_k\wedge T}-X_{s_k\wedge T})\smallskip\\ &\displaystyle =&\displaystyle \sum_{k=1}^n(X_{t_k}-X_{s_k})+(X_T-X_{s_{n+1}\wedge T})\smallskip\\ &\displaystyle \ge &\displaystyle (b-a)U[a,b]-\max(a-X_T,0). \end{array}$

The process ${\xi}$ takes only the values 0 and 1, so is equal to ${\xi=1_A}$ for an elementary predictable set of the form (2). This gives the following bound for the upcrossings of a process which, by the results of the previous post, is particularly suited to martingale convergence results.

Lemma 2 Let ${X_t}$ be a stochastic process with time ${t}$ running over the finite index set ${\mathbb{T}\subseteq{\mathbb R}}$ , and set ${T=\max\mathbb{T}}$ . Then there exists an elementary set A of the form (2) such that

$\displaystyle (b-a)U[a,b]\le \int 1_A\,dX+\max(a-X_T,0)$ (3)

Martingale Convergence

The considerations above lead to the following bound on the expected number of upcrossings of a martingale.

Lemma 3 (Doob’s upcrossing lemma) Let ${X_t}$ be a supermartingale with time ${t}$ running through a countable index set ${\mathbb{T}}$ . The number of upcrossings of any ${a<b}$ satisfies

$\displaystyle (b-a){\mathbb E}\left[U[a,b]\right]\le\sup_{t\in\mathbb{T}}{\mathbb E}\left[(a-X_t)\vee 0\right].$

Proof: It is enough to prove this for finite index sets ${\mathbb{T}}$ . The result for countably infinite sets then follows by taking a sequence ${\mathbb{T}_n\subseteq\mathbb{T}}$ of finite sets increasing to ${\mathbb{T}}$ and applying monotone convergence.

So, suppose that ${\mathbb{T}}$ is finite and set ${T=\max\mathbb{T}}$ . Equation (3) can be applied.

$\displaystyle (b-a){\mathbb E}\left[U[a,b]\right]\le{\mathbb E}\left[\int 1_A\,dX\right]+{\mathbb E}\left[(a-X_T)\vee 0\right]\le{\mathbb E}\left[(a-X_T)\vee 0\right].$

The second inequality follows from the fact that ${X}$ is a supermartingale (equivalently, ${-X}$ is a submartingale) and ${1_A}$ is a bounded nonnegative elementary predictable process. ⬜

Martingale convergence is a consequence of the upcrossing lemma. The following says that any ${L^1}$ -bounded martingale ${X_n}$ in discrete time converges almost surely.

Theorem 4 (Doob’s Forward Convergence Theorem) Let ${(X_n)_{n=1,2,\ldots}}$ be a martingale (or submartingale, or supermartingale) such that ${\mathbb{E}[|X_n|]}$ is bounded over all ${n\in\mathbb{N}}$ . Then, with probability one, the limit ${X_\infty=\lim_{n\rightarrow\infty}X_n}$ exists and is finite.

Proof: It is enough to consider the case where ${X}$ is a supermartingale, as the submartingale case then follows by applying the result to ${-X}$ . In this case, Lemma 3 shows that the expected number of upcrossings of any ${a<b}$ is finite, so ${U[a,b]<\infty}$ almost surely. By countable additivity, ${U[a,b]<\infty}$ simultaneously for all rational ${a<b}$ (and therefore, for all real ${a<b}$ ) with probability one. Consequently, the limit ${X_\infty=\lim_nX_n}$ exists in the extended real numbers, and Fatou’s lemma gives

$\displaystyle {\mathbb E}[|X_\infty|]\le\limsup_{n\rightarrow\infty}{\mathbb E}[|X_n|]<\infty,$

so ${X_\infty}$ is almost surely finite. ⬜

A process X is said to be uniformly integrable if the set of random variables ${\{X_t\colon t\in\mathbb{T}\}}$ is uniformly integrable. This case is particularly nice.

Corollary 5 Let ${(X_n)_{n=1,2,\ldots}}$ be a uniformly integrable martingale and let ${\mathcal{F}_\infty=\sigma(\bigcup_n\mathcal{F}_n)}$ be the sigma-algebra at infinity. Then, there is an almost-surely unique and integrable ${\mathcal{F}_\infty}$ -measurable random variable ${X_\infty}$ such that ${X_n={\mathbb E}[X_\infty\mid\mathcal{F}_n]}$ for each ${n}$ . Furthermore, ${X_n\rightarrow X_\infty}$ as ${n\rightarrow\infty}$ , with probability one.

Proof: First, by Doob’s forward convergence theorem, we can set ${X_\infty=\lim_nX_n}$ , which exists with probability one. By uniform integrability, this converges in ${L^1}$ and it follows that ${X_n={\mathbb E}[X_m\mid\mathcal{F}_n]}$ converges to ${{\mathbb E}[X_\infty\mid\mathcal{F}_n]}$ as ${m\rightarrow\infty}$ . So, ${X_\infty}$ satisfies the required properties.

Suppose ${X^\prime_\infty}$ is any other random variable satisfying the required properties. Then, ${{\mathbb E}[1_AX_\infty]={\mathbb E}[1_AX^\prime_\infty]={\mathbb E}[1_AX_n]}$ for any ${n}$ and ${A\in\mathcal{F}_n}$ . By the monotone class theorem, this extends to all ${A\in\mathcal{F}_\infty}$ . As ${X_\infty,X^\prime_\infty}$ are ${\mathcal{F}_\infty}$ -measurable, it follows that they are almost surely equal. ⬜

The condition that ${X_n}$ is ${L^1}$ -bounded in Doob’s forward convergence theorem is automatically satisfied in many cases. In particular, if ${X}$ is a non-negative supermartingale then ${\mathbb{E}[|X_n|]=\mathbb{E}[X_n]\le\mathbb{E}[X_1]}$ for all ${n\ge 1}$ , so ${\mathbb{E}[|X_n|]}$ is bounded, giving the following corollary.

Corollary 6 Let ${(X_n)_{n\in\mathbb{N}}}$ be a non-negative martingale (or supermartingale). Then, with probability one, the limit ${X_\infty=\lim_{n\rightarrow\infty}X_n}$ exists and is finite.

As an example application of the martingale convergence theorem, it is easy to show that a standard random walk started started at ${0}$ will visit every level with probability one.

Corollary 7 Let ${(X_n)_{n\in\mathbb{N}}}$ be a standard random walk. That is, ${X_1=0}$ and

$\displaystyle \mathbb{P}(X_{n+1}=X_n+1\mid \mathcal{F}_n)=\mathbb{P}(X_{n+1}=X_n-1\mid\mathcal{F}_n) = 1/2.$

Then, for every integer ${a}$ , with probability one ${X_n=a}$ for some ${n}$ .

Proof: Without loss of generality, suppose that ${a\le 0}$ . Let ${T:\Omega\rightarrow\mathbb{N}\cup\{\infty\}}$ be the first time ${n}$ for which ${X_n=a}$ . It is easy to see that the stopped process ${X^T_n}$ defined by ${X^T_n=X_{\min(n,T)}}$ is a martingale and ${X^T-a}$ is non-negative. Therefore, by the martingale convergence theorem, the limit ${X^T_\infty=\lim_{n\rightarrow\infty}X^T_n}$ exists and is finite (almost surely). In particular, ${|X^T_{n+1}-X^T_n|}$ converges to ${0}$ and must be less than ${1}$ for large ${n}$ . However, ${|X^T_{n+1}-X^T_n|=1}$ whenever ${n < T}$ , so we have ${T<\infty}$ and therefore ${X_n=a}$ for some ${n}$ . ⬜

Levy’s Upwards and Downwards Theorems

A very useful application of martingale convergence is to the following results concerning limits of conditional expectations for a limit of increasing or decreasing sigma-algebras.

Theorem 8 (Levy’s upward theorem) Let ${(\Omega,\mathcal{F},{\mathbb P})}$ be a probability space and ${\{\mathcal{F}_n\}_{n\in{\mathbb N}}}$ be an increasing sequence of sub-sigma-algebras of ${\mathcal{F}}$ . Set ${\mathcal{F}_\infty\equiv\sigma\left(\bigcup_n\mathcal{F}_n\right)}$ . For any integrable random variable ${X}$ , the following limit holds with probability one,

$\displaystyle {\mathbb E}[X\mid\mathcal{F}_n]\rightarrow{\mathbb E}[X\mid\mathcal{F}_\infty]$

as ${n\rightarrow\infty}$ . This limit also holds under ${L^1}$ -convergence.

Theorem 9 (Levy’s downward theorem) Let ${(\Omega,\mathcal{F},{\mathbb P})}$ be a probability space and ${\{\mathcal{F}_n\}_{n\in{\mathbb N}}}$ be a decreasing sequence of sub-sigma-algebras of ${\mathcal{F}}$ . Set ${\mathcal{F}_\infty\equiv\bigcap_n\mathcal{F}_n}$ . For any integrable random variable ${X}$ , the following limit holds with probability one,

$\displaystyle {\mathbb E}[X\mid\mathcal{F}_n]\rightarrow{\mathbb E}[X\mid\mathcal{F}_\infty]$

as ${n\rightarrow\infty}$ . This limit also holds under ${L^1}$ -convergence.

The upwards theorem is nothing more than a direct application of the convergence theorem for uniformly integrable martingales. The downwards theorem follows in a similar way.

For each negative integer ${n}$ , set ${\mathcal{G}_n=\mathcal{F}_{-n}}$ and ${X_n={\mathbb E}[X\mid\mathcal{G}_n]}$ . This is a martingale with respect to the filtration ${\mathcal{G}_n}$ and, by Doob’s upcrossing lemma, almost surely has finitely many upcrossings of any interval ${a<b}$ . So the limit ${X_{-\infty}=\lim_{n\rightarrow-\infty}X_n}$ exists almost-surely. By uniform integrability of conditional expectations, this must also converge in the ${L^1}$ -norm. In particular, ${X_{-\infty}}$ is integrable, and taking limits of the equality ${{\mathbb E}[X\mid\mathcal{F}_\infty]={\mathbb E}[X_{-n}\mid\mathcal{F}_\infty]}$ gives

$\displaystyle {\mathbb E}[X\mid\mathcal{F}_\infty]=\lim_{n\rightarrow\infty}{\mathbb E}[X_{-n}\mid\mathcal{F}_{\infty}]={\mathbb E}[X_{-\infty}\mid\mathcal{F}_\infty]=X_{-\infty},$

proving Levy’s downwards theorem.

Note that, due to the uniformly integrability of conditional expectations, ${L^1}$ -convergence immediately follows from almost-sure convergence in Levy’s upwards and downwards theorems.

The Strong Law of Large Numbers

Roughly speaking, the strong law of large numbers says that the sample mean of a set of independent and identically distributed random variables tends to the mean, with probability one, as the sample size tends to infinity.

More precisely, this can be stated as follows. Suppose that ${X_1,X_2,\ldots}$ is a sequence of IID random variables. Set ${S_n\equiv X_1+X_2+\cdots+X_n}$ . If the random variables ${X_k}$ are integrable with mean ${\mu}$ then

$\displaystyle S_n/n\rightarrow\mu$

with probability one as ${n\rightarrow\infty}$ . There is also a weak law of large numbers which states that the limit above holds in probability. However, as convergence in probability always follows from almost sure convergence, the weak law is a direct consequence of the strong law.

I mention the strong law as an example of a well-known result which is quite hard to prove from elementary ideas, but follows easily from martingale convergence. The strong law actually follows from Levy’s downwards theorem.

For each ${n}$ set ${\mathcal{F}_n=\sigma(S_{n},S_{n+1},\ldots)}$ . Symmetry under permuting ${X_1,X_2,\ldots,X_n}$ gives

$\displaystyle {\mathbb E}[X_1\mid\mathcal{F}_n]={\mathbb E}[X_2\mid\mathcal{F}_n]=\cdots={\mathbb E}[X_n\mid\mathcal{F}_n].$

Taking the average of these terms,

$\displaystyle {\mathbb E}[X_1\mid\mathcal{F}_n]=S_n/n.$

So, setting ${\mathcal{F}_\infty=\bigcap_n\mathcal{F}_n}$ , Levy’s downwards theorem shows that ${S_n/n\rightarrow{\mathbb E}[X_1\mid\mathcal{F}_\infty]}$ with probability one, and this limit is a random variable with mean ${\mu}$ . The final step is to apply Kolmogorov’s zero-one law. This implies that the limit of ${S_n/n}$ is almost-surely constant, so must equal ${\mu}$ .

Published by George Lowther

View all posts by George Lowther

Published 6 December 0928 February 23

19 thoughts on “Upcrossings, Downcrossings, and Martingale Convergence”

TheBridge says:

17 October 11 at 2:41 PM

Hi,

As I was reading (once more) your blog, I have a few remarks about this article,

I noticed that you mention a set $B$ in lemma 2 which does not appear (anymore ?) in the equation (3) (or (4) ?) .

(Maybe related to the preceding remark) In the proof of lemma 3, you mention a second inequality which is missing in the claim.

After the proof of Theorem 4, you make the following statement that I don’t really understand :

“A process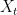 $X_t$ is uniformly integrable if each of the random variables 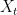$X_t$ are uniformly integrable.” As uniform integrability is usually about a family of random variables, I don’t really see what you mean by “each 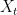$X_t$ is uniformly integrable unless this is only the statement that an integrable random variable is uniformly integrable.

Best Regards

Reply
1. George Lowther says:
  
  18 October 11 at 1:15 AM
  
  Yeah, this is rather sloppy. I’ll edit it when I have time. [Edit: This is fixed now] About the uniform integrability, I should have said “…if the set of random variables {X_t: t ∈ R₊} is uniformly integrable”. And, the set B isn’t used, it should be deleted. Thanks for pointing these out.
  
  Reply
nguyen says:

4 November 11 at 5:14 PM

Dear George

thanks for your great block, I learn a lot from your blog. I would like to have a question :
you wrote
symmetry under permuting ${X_1,X_2,\ldots,X_n}$ gives

$\displaystyle {\mathbb E}[X_1\mid\mathcal{F}_n]={\mathbb E}[X_2\mid\mathcal{F}_n]=\cdots={\mathbb E}[X_n\mid\mathcal{F}_n].$

can you explain more on this ? why you have above “equal signs” ?

thanks

Reply
1. TheBridge says:
  
  7 November 11 at 2:45 PM
  
  Hi ngyuen,
  
  This follows from the following lemma :
  
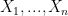  If you are given a symmetric function $f(x_1,...,x_n)$ and $X_1,...,X_n$ i.i.d. integrable random variables (or positive) then $\mathbb{E}[X_i|\sigma(f(X_1,...,X_n))]=\mathbb{E}[X_j | \sigma(f(X_1,...,X_n))]$ almost surely for every $i,j=1,...n$ .
  
  Then take $n.f(x_1,...,x_n)=\sum_{i=1}^{n} x_i=S_n$ and you have almost what you are looking for. To finish the work neatly you have to notice that $\mathbb{E}[ X_i |\mathcal{F}_n]=\mathbb{E}[ X_i |\sigma(f(X_1,...,X_n))]$ almost surely for $i=1,...,n$ by noting that $\mathcal{F}_n= \sigma(S_n) \vee \sigma( (X_j)_{j>n} )$ , and that $X_j$ is independent of $S_n$ for every $j>n$ .
  
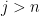  You should try to prove the lemma by going back to definition of conditional expectation, using the symmetry of $f$ and the fact that $X_i$ are i.i.d. and integrable together with the following hint :
  
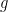  when conditioning with respect to some real integrable random variable $Y$ , for every bounded random variable $X$ then there exists a measurable function $g$ such that $E[X| Y]=g(Y)$ almost surely.
  
  I hope it helps you and that this reply will save some time to George Lowther so he can write some new great posts 😉
  
  Best regards
  
  Reply
  1. George Lowther says:
    
    7 November 11 at 9:52 PM
    
    TheBridge: Thanks! I’ll add that here we have f(X₁,…,X_n) = X₁+ ⋯ +X_n. So, the equality come down to showing that 𝔼[X_i g(X₁+⋯+X_n)] = 𝔼[X_j g(X₁+⋯+X_n)] for bounded measurable functions g. This follows from symmetry of the distribution of (X₁,…,X_n).
    
    Reply
Tigran says:

7 December 11 at 6:39 PM

Dear Goerge,

I am curious as to whether we don’t need to make sure that the times at which an elementary process has jumps need to be stopping times in order for this process to be adapted.
For example, the times s_k and t_k defined before lemma 2 don’t seem to be necessarily stopping times, and so I am somewhat confused as to what the filtration F_{s_k} and F_{t_k} would be.
By the way thanks again for the reply about the joint measurability in a previous post. It was very useful.

Reply
1. Tigran says:
  
  8 December 11 at 9:39 AM
  
  Actually the problem is resolved if the time domain of X_t is finite, which might be what you are assuming implicitly.
  
  Reply
  1. TheBridge says:
    
    8 December 11 at 12:51 PM
    
    Hi Tigran,
    
    Here all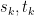 $s_k,t_k$ are deterministic and bounded by T, so there is no stopping time issue (notice however that so they are trivial stopping times).
    George Lowther might confirm this, but in the context of these notes, elementary predictable processes do not use stopping times in their definition, only deterministic times (check “Martingales and Elementary Integrals” post). But it is true that other authers use them to define elementary process (for example in Protter’s book) maybe this is where your question is coming from.
    
    Best Regards
    
    Reply
    1. George Lowther says:
      
      8 December 11 at 1:52 PM
      
      TheBridge: Thanks for that comment, it more or less covers what I was thinking too. I’ll add also that, in lemma 2 (and the bit just before its statement) the times are stopping times. This only works because the index set here is finite. Also, because the index set is finite, the set in (2) can be written as a union over a finite set of deterministic times, so is elementary (I could have stated this more clearly in the post).
      
      As you mention, the definition of elementary sets and processes is not standardised and differs between texts. Sometimes “simple” is used instead. I tend to use elementary to refer to processes defined using a finite set of deterministic times and simple for the same thing with stopping times. There was no need to consider simple processes here, so I haven’t used them in these notes.
    2. Tigran says:
      
      10 December 11 at 1:58 PM
      
      Thanks for your feedback. The reason I asked is that this also comes up further in the notes (e.g. the proof of cadlag versions in the next post), where things seem to rely on the finiteness of the index set to make the hitting times of X_t stopping times, and then extend it to countable sets using the MCT.
ConradoConrado says:

29 September 17 at 10:02 AM

Hi,
Where one reads

“Note that between any two upcrossings there is a downcrossing and, similarly, there is a downcrossing between any two upcrossings.”

Shouldn’t it be

Note that between any two upcrossings there is a downcrossing and, similarly, there is a upcrossing between any two downcrossing.

?

Reply
1. George Lowther says:
  
  29 September 17 at 10:51 AM
  
  Ha! Of course. I’ll correct it. Thanks
  
  Reply
Pingback: How to compute the time of upward movement of a Brownian motion – Math Solution
RozaTh says:

26 April 22 at 6:48 AM

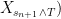Hi, The second line of the equations before Lemma 2, reads $\displaystyle \sum_{k=1}^n(X_{t_k}-X_{s_k})+(X_T-X_{s_n\wedge T})$ . Shouldn’t the last term be $\displaystyle X_{s_{n+1}\wedge T})$ ?

Reply
1. George Lowther says:
  
  27 April 22 at 9:24 PM
  
  Fixed. Thanks!
  
  Reply
Pingback: stochastic processes - Martigale that maximizes its expected number of upcrossings/downcrossings Answer - Lord Web
ARS says:

4 February 23 at 8:30 AM

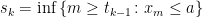Hey! Really nice post and blog! When you say $s_k=\inf\left\{m\ge t_{k-1}\colon X_{m}\le a\right\}$ , I think it should be $s_k=\inf\left\{m\ge t_{k-1}\colon x_{m}\le a\right\}$ , idem for $t.$

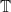Also, the “proposition” if ${X_{s}\le a<b\le X_{t}}$ for times $s<t$ in $\mathbb{T}$ , then ${s\le s_k0$ , right? Otherwise, as $t_0=0$ , one can construct trivial counterexamples isn’t it?

Reply
1. ARS says:
  
  5 February 23 at 8:57 AM
  
  It should read: […] then $s \le s_k<t_k \le t$ for some $k$ , is only true if $s\ge0$ , right? […]
  
  Reply
2. George Lowther says:
  
  28 February 23 at 2:09 AM
  
  Thanks! I fixed the first point. For the second, I was assuming the time index set starts at 0 for part of the proof, but I had relaxed this assumption so it is a bit inconsistent. I will reword it when ‘I have some time
  
  Reply

	Harry on Filtrations and Adapted P…
	Anonymous on Analytic Sets
	Daniel on Analytic Sets
	Sid on Martingale Convergence
	northwiz on Preservation of the Local Mart…
	George Lowther on Martingale Convergence
	Sid on Martingale Convergence
	George Lowther on The Burkholder-Davis-Gundy Ine…
	George Lowther on Preservation of the Local Mart…
	northwiz on Preservation of the Local Mart…

Martingale Convergence

Levy’s Upwards and Downwards Theorems

The Strong Law of Large Numbers

Like this:

Related

Published by George Lowther

19 thoughts on “Upcrossings, Downcrossings, and Martingale Convergence”

Leave a Reply to George Lowther Cancel reply