Tag: Martingale

Martingale Marginals

[This post originates from twitter threads posted on 9 Sep 21 and 2 Feb 22.]

A while ago, I proved the result: A continuous strong Markov martingale is uniquely determined by its marginal distributions. This is discussed in a recent paper by Beiglböck, Pammer, and Schachermayer.

Time for a thread discussing some of these ideas, which have been studied for decades in both stochastic calculus and mathematical finance. Continue reading “Martingale Marginals” →

A Process With Hidden Drift

Consider a stochastic process X of the form

\displaystyle X_t=W_t+\int_0^t\xi_sds, (1)

for a standard Brownian motion W and predictable process {\xi}, defined with respect to a filtered probability space {(\Omega,\mathcal F,\{\mathcal F_t\}_{t\in{\mathbb R}_+},{\mathbb P})}. For this to make sense, we must assume that {\int_0^t\lvert\xi_s\rvert ds} is almost surely finite at all times, and I will suppose that {\mathcal F_\cdot} is the filtration generated by W.

The question is whether the drift {\xi} can be backed out from knowledge of the process X alone. As I will show with an example, this is not possible. In fact, in our example, X will itself be a standard Brownian motion, even though the drift {\xi} is non-trivial (that is, {\int\xi dt} is not almost surely zero). In this case X has exactly the same distribution as W, so cannot be distinguished from the driftless case with {\xi=0} by looking at the distribution of X alone.

On the face of it, this seems rather counter-intuitive. By standard semimartingale decomposition, it is known that we can always decompose

\displaystyle X=M+A (2)

for a unique continuous local martingale M starting from zero, and unique continuous FV process A. By uniqueness, {M=W} and {A=\int\xi dt}. This allows us to back out the drift {\xi} and, in particular, if the drift is non-trivial then X cannot be a martingale. However, in the semimartingale decomposition, it is required that M is a martingale with respect to the original filtration {\mathcal F_\cdot}. If we do not know the filtration {\mathcal F_\cdot}, then it might not be possible to construct decomposition (2) from knowledge of X alone. As mentioned above, we will give an example where X is a standard Brownian motion which, in particular, means that it is a martingale under its natural filtration. By the semimartingale decomposition result, it is not possible for X to be an {\mathcal F_\cdot}-martingale. A consequence of this is that the natural filtration of X must be strictly smaller than the natural filtration of W.

The inspiration for this post was a comment by Gabe posing the following question: If we take {\mathbb F} to be the filtration generated by a standard Brownian motion W in {(\Omega,\mathcal F,{\mathbb P})}, and we define {\tilde W_t=W_t+\int_0^t\Theta_udu}, can we find an {\mathbb F}-adapted {\Theta} such that the filtration generated by {\tilde W} is smaller than {\mathbb F}? Our example gives an affirmative answer. Continue reading “A Process With Hidden Drift” →

A Martingale Which Moves Along a Deterministic Path

Sample Paths
Figure 1: Sample paths

In this post I will construct a continuous and non-constant martingale M which only varies on the path of a deterministic function {f\colon{\mathbb R}_+\rightarrow{\mathbb R}}. That is, {M_t=f(t)} at all times outside of the set of nontrivial intervals on which M is constant. Expressed in terms of the stochastic integral, {dM_t=0} on the set {\{t\colon M_t\not=f(t)\}} and,

\displaystyle M_t = \int_0^t 1_{\{M_s=f(s)\}}\,dM_s. (1)

In the example given here, f will be right-continuous. Examples with continuous f do exist, although the constructions I know of are considerably more complicated. At first sight, these properties appear to contradict what we know about continuous martingales. They vary unpredictably, behaving completely unlike any deterministic function. It is certainly the case that we cannot have {M_t=f(t)} across any interval on which M is not constant.

By a stochastic time-change, any Brownian motion B can be transformed to have the same distribution as M. This means that there exists an increasing and right-continuous process A adapted to the same filtration as B and such that {B_t=M_{A_t}} where M is a martingale as above. From this, we can infer that

\displaystyle B_t=f(A_t),

expressing Brownian motion as a function of an increasing process. Continue reading “A Martingale Which Moves Along a Deterministic Path” →

Do Convex and Decreasing Functions Preserve the Semimartingale Property?

Some years ago, I spent considerable effort trying to prove the hypothesis below. After failing at this, I spent time trying to find a counterexample, but also with no success. I did post this as a question on mathoverflow, but it has so far received no conclusive answers. So, as far as I am aware, the following statement remains unproven either way.

Hypothesis H1 Let {f\colon{\mathbb R}_+\times{\mathbb R}\rightarrow{\mathbb R}} be such that {f(t,x)} is convex in x and right-continuous and decreasing in t. Then, for any semimartingale X, {f(t,X_t)} is a semimartingale.

It is well known that convex functions of semimartingales are themselves semimartingales. See, for example, the Ito-Tanaka formula. More generally, if {f(t,x)} was increasing in t rather than decreasing, then it can be shown without much difficulty that {f(t,X_t)} is a semimartingale. Consider decomposing {f(t,X_t)} as

\displaystyle f(t,X_t)=\int_0^tf_x(s,X_{s-})\,dX_s+V_t, (1)

for some process V. By convexity, the right hand derivative of {f(t,x)} with respect to x always exists, and I am denoting this by {f_x}. In the case where f is twice continuously differentiable then the process V is given by Ito’s formula which, in particular, shows that it is a finite variation process. If {f(t,x)} is convex in x and increasing in t, then the terms in Ito’s formula for V are all increasing and, so, it is an increasing process. By taking limits of smooth functions, it follows that V is increasing even when the differentiability constraints are dropped, so {f(t,X_t)} is a semimartingale. Now, returning to the case where {f(t,x)} is decreasing in t, Ito’s formula is only able to say that V is of finite variation, and is generally not monotonic. As limits of finite variation processes need not be of finite variation themselves, this does not say anything about the case when f is not assumed to be differentiable, and does not help us to determine whether or not {f(t,X_t)} is a semimartingale.

Hypothesis H1 can be weakened by restricting to continuous functions of continuous martingales.

Hypothesis H2 Let {f\colon{\mathbb R}_+\times{\mathbb R}\rightarrow{\mathbb R}} be such that {f(t,x)} is convex in x and continuous and decreasing in t. Then, for any continuous martingale X, {f(t,X_t)} is a semimartingale.

As continuous martingales are special cases of semimartingales, hypothesis H1 implies H2. In fact, the reverse implication also holds so that hypotheses H1 and H2 are equivalent.

Hypotheses H1 and H2 can also be recast as a simple real analysis statement which makes no reference to stochastic processes.

Hypothesis H3 Let {f\colon{\mathbb R}_+\times{\mathbb R}\rightarrow{\mathbb R}} be such that {f(t,x)} is convex in x and decreasing in t. Then, {f=g-h} where {g(t,x)} and {h(t,x)} are convex in x and increasing in t.

Continue reading “Do Convex and Decreasing Functions Preserve the Semimartingale Property?” →

Failure of the Martingale Property For Stochastic Integration

If X is a cadlag martingale and {\xi} is a uniformly bounded predictable process, then is the integral

\displaystyle Y=\int\xi\,dX (1)

a martingale? If {\xi} is elementary this is one of most basic properties of martingales. If X is a square integrable martingale, then so is Y. More generally, if X is an {L^p}-integrable martingale, any {p > 1}, then so is Y. Furthermore, integrability of the maximum {\sup_{s\le t}\lvert X_s\rvert} is enough to guarantee that Y is a martingale. Also, it is a fundamental result of stochastic integration that Y is at least a local martingale and, for this to be true, it is only necessary for X to be a local martingale and {\xi} to be locally bounded. In the general situation for cadlag martingales X and bounded predictable {\xi}, it need not be the case that Y is a martingale. In this post I will construct an example showing that Y can fail to be a martingale. Continue reading “Failure of the Martingale Property For Stochastic Integration” →

Martingales with Non-Integrable Maximum

It is a consequence of Doob’s maximal inequality that any {L^p}-integrable martingale has a maximum, up to a finite time, which is also {L^p}-integrable for any {p > 1}. Using {X^*_t\equiv\sup_{s\le t}\lvert X_s\rvert} to denote the running absolute maximum of a cadlag martingale X, then {X^*} is {L^p}-integrable whenever {X} is. It is natural to ask whether this also holds for {p=1}. As martingales are integrable by definition, this is just asking whether cadlag martingales necessarily have an integrable maximum. Integrability of the maximum process does have some important consequences in the theory of martingales. By the Burkholder-Davis-Gundy inequality, it is equivalent to the square-root of the quadratic variation, {[X]^{1/2}}, being integrable. Stochastic integration over bounded integrands preserves the martingale property, so long as the martingale has integrable maximal process. The continuous and purely discontinuous parts of a martingale X are themselves local martingales, but are not guaranteed to be proper martingales unless X has integrable maximum process.

The aim of this post is to show, by means of some examples, that a cadlag martingale need not have an integrable maximum. Continue reading “Martingales with Non-Integrable Maximum” →

The Optimality of Doob’s Maximal Inequality

One of the most fundamental and useful results in the theory of martingales is Doob’s maximal inequality. Use {X^*_t\equiv\sup_{s\le t}\lvert X_s\rvert} to denote the running (absolute) maximum of a process X. Then, Doob’s {L^p} maximal inequality states that, for any cadlag martingale or nonnegative submartingale X and real {p > 1},

\displaystyle \lVert X^*_t\rVert_p\le c_p \lVert X_t\rVert_p (1)

with {c_p=p/(p-1)}. Here, {\lVert\cdot\rVert_p} denotes the standard Lp-norm, {\lVert U\rVert_p\equiv{\mathbb E}[U^p]^{1/p}}.

An obvious question to ask is whether it is possible to do any better. That is, can the constant {c_p} in (1) be replaced by a smaller number. This is especially pertinent in the case of small p, since {c_p} diverges to infinity as p approaches 1. The purpose of this post is to show, by means of an example, that the answer is no. The constant {c_p} in Doob’s inequality is optimal. We will construct an example as follows.

Example 1 For any {p > 1} and constant {1 \le c < c_p} there exists a strictly positive cadlag {L^p}-integrable martingale {\{X_t\}_{t\in[0,1]}} with {X^*_1=cX_1}.

For X as in the example, we have {\lVert X^*_1\rVert_p=c\lVert X_1\rVert_p}. So, supposing that (1) holds with any other constant {\tilde c_p} in place of {c_p}, we must have {\tilde c_p\ge c}. By choosing {c} as close to {c_p} as we like, this means that {\tilde c_p\ge c_p} and {c_p} is indeed optimal in (1). Continue reading “The Optimality of Doob’s Maximal Inequality” →

The Maximum Maximum of Martingales with Known Terminal Distribution

In this post I will be concerned with the following problem — given a martingale X for which we know the distribution at a fixed time, and we are given nothing else, what is the best bound we can obtain for the maximum of X up until that time? This is a question with a long history, starting with Doob’s inequalities which bound the maximum in the 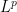{L^p} norms and in probability. Later, Blackwell and Dubins (3), Dubins and Gilat (5) and Azema and Yor (1,2) showed that the maximum is bounded above, in stochastic order, by the Hardy-Littlewood transform of the terminal distribution. Furthermore, this bound is the best possible in the sense that there do exists martingales for which it can be attained, for any permissible terminal distribution. Hobson (7,8) considered the case where the starting law is also known, and this was further generalized to the case with a specified distribution at an intermediate time by Brown, Hobson and Rogers (4). Finally, Henry-Labordère, Obłój, Spoida and Touzi (6) considered the case where the distribution of the martingale is specified at an arbitrary set of times. In this post, I will look at the case where only the terminal distribution is specified. This leads to interesting constructions of martingales and, in particular, of continuous martingales with specified terminal distributions, with close connections to the Skorokhod embedding problem.

I will be concerned with the maximum process of a cadlag martingale X,

\displaystyle X^*_t=\sup_{s\le t}X_s,

which is increasing and adapted. We can state and prove the bound on 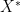{X^*} relatively easily, although showing that it is optimal is more difficult. As the result holds more generally for submartingales, I state it in this case, although I am more concerned with martingales here.

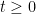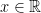Theorem 1 If X is a cadlag submartingale then, for each {t\ge0} and {x\in{\mathbb R}},

\displaystyle {\mathbb P}\left(X^*_t\ge x\right)\le\inf_{y < x}\frac{{\mathbb E}\left[(X_t-y)_+\right]}{x-y}. (1)

Proof: We just need to show that the inequality holds for each 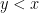{y < x}, and then it immediately follows for the infimum. Choosing {y < x^\prime < x}, consider the stopping time

\displaystyle \tau=\inf\{s\ge0\colon X_s\ge x^\prime\}.

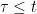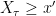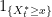Then, {\tau \le t} and {X_\tau\ge x^\prime} whenever {X^*_t \ge x}. As {f(z)\equiv(z-y)_+} is nonnegative and increasing in z, this means that {1_{\{X^*_t\ge x\}}} is bounded above by {f(X_{\tau\wedge t})/f(x^\prime)}. Taking expectations,

\displaystyle {\mathbb P}\left(X^*_t\ge x\right)\le{\mathbb E}\left[f(X_{\tau\wedge t})\right]/f(x^\prime).

Since f is convex and increasing, {f(X)} is a submartingale so, using optional sampling,

\displaystyle {\mathbb P}\left(X^*_t\ge x\right)\le{\mathbb E}\left[f(X_t)\right]/f(x^\prime).

Letting {x^\prime} increase to {x} gives the result. ⬜

The bound stated in Theorem 1 is also optimal, and can be achieved by a continuous martingale. In this post, all measures on 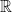{{\mathbb R}} are defined with respect to the Borel sigma-algebra.

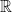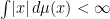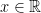Theorem 2 If {\mu} is a probability measure on {{\mathbb R}} with {\int\lvert x\rvert\,d\mu(x) < \infty} and {t > 0} then there exists a continuous martingale X (defined on some filtered probability space) such that {X_t} has distribution {\mu} and (1) is an equality for all {x\in{\mathbb R}}.

Continue reading “The Maximum Maximum of Martingales with Known Terminal Distribution” →

The Doob-Meyer Decomposition for Quasimartingales

As previously discussed, for discrete-time processes the Doob decomposition is a simple, but very useful, technique which allows us to decompose any integrable process into the sum of a martingale and a predictable process. If {\{X_n\}_{n=0,1,2,\ldots}} is an integrable discrete-time process adapted to a filtration {\{\mathcal{F}_n\}_{n=0,1,2,\ldots}}, then the Doob decomposition expresses X as

\displaystyle \setlength\arraycolsep{2pt} \begin{array}{rl} \displaystyle X_n&\displaystyle=M_n+A_n,\smallskip\\ \displaystyle A_n&\displaystyle=\sum_{k=1}^n{\mathbb E}\left[X_k-X_{k-1}\;\vert\mathcal{F}_{k-1}\right]. \end{array} (1)

Then, M is then a martingale and A is an integrable process which is also predictable, in the sense that {A_n} is {\mathcal{F}_{n-1}}-measurable for each {n > 0}. The expected value of the variation of A can be computed in terms of X,

\displaystyle {\mathbb E}\left[\sum_{k=1}^n\lvert A_k-A_{k-1}\rvert\right] ={\mathbb E}\left[\sum_{k=1}^n\left\lvert {\mathbb E}[X_k-X_{k-1}\vert\;\mathcal{F}_{k-1}]\right\rvert\right].

This is the mean variation of X.

In continuous time, the situation is rather more complex, and will require constraints on the process X other than just integrability. We have already discussed the case for submartingales — the Doob-Meyer decomposition. This decomposes a submartingale into a local martingale and a predictable increasing process.

A natural setting for further generalising the Doob-Meyer decomposition is that of quasimartingales. In continuous time, the appropriate class of processes to use for the component A of the decomposition is the predictable FV processes. Decomposition (2) below is the same as that in the previous post on special semimartingales. This is not surprising, as we have already seen that the class of special semimartingales is identical to the class of local quasimartingales. The difference with the current setting is that we can express the expected variation of A in terms of the mean variation of X, and obtain a necessary and sufficient condition for the local martingale component to be a proper martingale.

As was noted in an earlier post, historically, decomposition (2) for quasimartingales played an important part in the development of stochastic calculus and, in particular, in the proof of the Bichteler-Dellacherie theorem. That is not the case in these notes, however, as we have already proven the main results without requiring quasimartingales. As always, any two processes are identified whenever they are equivalent up to evanescence.

Theorem 1 Every cadlag quasimartingale X uniquely decomposes as

\displaystyle X=M+A (2)

where M is a local martingale and A is a predictable FV process with {A_0=0}. Then, A has integrable variation over each finite time interval {[0,t]} satisfying

\displaystyle {\rm Var}_t(X)={\rm Var}_t(M)+{\mathbb E}\left[\int_0^t\,\vert dA\vert\right]. (3)

so that, in particular,

\displaystyle {\mathbb E}\left[\int_0^t\,\vert dA\vert\right]\le{\rm Var}_t(X). (4)

Furthermore, the following are equivalent,

  1. X is of class (DL).
  2. M is a proper martingale.
  3. inequality (4) is an equality for all times t.

Continue reading “The Doob-Meyer Decomposition for Quasimartingales” →

Properties of Quasimartingales

The previous two posts introduced the concept of quasimartingales, and noted that they can be considered as a generalization of submartingales and supermartingales. In this post we prove various basic properties of quasimartingales and of the mean variation, extending results of martingale theory to this situation.

We start with a version of optional stopping which applies for quasimartingales. For now, we just consider simple stopping times, which are stopping times taking values in a finite subset of the nonnegative extended reals {\bar{\mathbb R}_+=[0,\infty]}. Stopping a process can only decrease its mean variation (recall the alternative definitions {{\rm Var}} and {{\rm Var}^*} for the mean variation). For example, a process X is a martingale if and only if {{\rm Var}(X)=0}, so in this case the following result says that stopped martingales are martingales.

Lemma 1 Let X be an adapted process and {\tau} be a simple stopping time. Then

\displaystyle {\rm Var}^*(X^\tau)\le{\rm Var}^*(X). (1)

Assuming, furthermore, that X is integrable,

\displaystyle {\rm Var}(X^\tau)\le{\rm Var}(X). (2)

and, more precisely,

\displaystyle {\rm Var}(X)={\rm Var}(X^\tau)+{\rm Var}(X-X^\tau) (3)

Continue reading “Properties of Quasimartingales” →