A major difference between standard integral calculus and stochastic calculus is the existence of quadratic variations and covariations. Such terms show up, for example, in the stochastic version of the integration by parts formula.
For motivation, let us start by considering a standard argument for differentiable processes. The increment of a process over a time step
can be written as
. The following identity is easily verified,
| (1) |
Now, divide the time interval into
equal parts. That is, set
for
. Then, using
and summing equation (1) over these times,
| (2) |
If the processes are continuously differentiable, then the final term on the right hand side is a sum of terms, each of order
, and therefore is of order
. This vanishes in the limit
, leading to the integration by parts formula
Now, suppose that are standard Brownian motions. Then,
are normal random variables with standard deviation
. It follows that the final term on the right hand side of (2) is a sum of
terms each of which is, on average, of order
. So, even in the limit as
goes to infinity, it does not vanish. Consequently, in stochastic calculus, the integration by parts formula requires an additional term, which is called the quadratic covariation (or, just covariation) of
and
.
There are several methods of defining quadratic variations, but my preferred approach is to use limits along partitions. A stochastic partition of the nonnegative real numbers
is taken to mean a sequence of stopping times, starting at zero and increasing to infinity in the limit,
| (3) |
Along such a partition, the approximation to the quadratic variation of
and the approximation
to the covariation of
and
is,
| (4) |
Note that the times are eventually constant and equal to
, so the sums above only contain finitely many nonzero terms. If
is a stochastic partition of
then
is a partition of the interval
. Its mesh is the longest subinterval
For stochastic partitions, this is a random variable. The quadratic variation and covariation are then equal to the limit of the approximations (4) as the mesh goes to zero. At any fixed time, this limit converges in probability. However, looking at the paths of the processes, the stronger property of uniform convergence on compacts in probability (ucp) is obtained. The proof is given further below.
Theorem 1 (Quadratic Variations and Covariations) Let
be semimartingales. Then, there exist cadlag adapted processes
and
satisfying the following.
For any sequence
of stochastic partitions of
such that, for each
, the mesh
tends to zero in probability as
, the following limits hold
(5) as
. Furthermore, convergence also holds in the semimartingale topology.
The process is called the quadratic variation of
and
is the (quadratic) covariation of
and
. Note that, as
is symmetric and bilinear in
with
, then the same holds for
. That is,
for semimartingales and real numbers
. It is clear that
. The following properties also follow easily from the definition. Recall that an FV process is a cadlag adapted process with almost surely finite variation over all bounded time intervals, and such processes are semimartingales.
Lemma 2
- If
is a semimartingale then
is a cadlag adapted and increasing processes.
- If
are semimartingales then
is an FV process.
Proof: Choose times . If
is any stochastic partition as in (3) with
for some
then,
Taking limits of such partitions gives as required. Then, the polarization identity expresses
as the difference of increasing processes and, as such, is an FV process. ⬜
In particular, quadratic variations variations and covariations are semimartingales. The following differential notation is sometimes used,
The stochastic version of the integration by parts formula is as follows. Sometimes, this result is used as the definition of quadratic covariations instead of using partitions as above.
Theorem 3 (Integration by Parts) If
are semimartingales then
(6)
The proof of this is given along with the existence of quadratic variations below. The special case with is often useful,
| (7) |
Note that, in differential notation (6) is simply
which is the stochastic differential version of equation (1). As is a semimartingale, the following corollary of the integration by parts formula is obtained.
Corollary 4 If
are semimartingales, then so is
.
Quadratic Variation of Brownian motion
As standard Brownian motion, , is a semimartingale, Theorem 1 guarantees the existence of the quadratic variation. To calculate
, any sequence of partitions whose mesh goes to zero can be used. For each
, the quadratic variation on a partition of
equally spaced subintervals of
is
The terms are normal with zero mean and variance
. So, their squares have mean
and variance
, giving the following for
,
The variance vanishes as goes to infinity,
. This gives the quadratic variation as simply
| (8) |
Using bilinearity of quadratic covariations, this result can be generalized to obtain the quadratic covariations of correlated Brownian motions. Two Brownian motions have correlation
if, for each
,
and
are independent of
and jointly normal with correlation
. That is, their covariance is
. If
for a constant
then it follows that
is normal with variance
If we choose then this shows that
is a standard Brownian motion, with quadratic variation given by (8). Bilinearity of covariations can be applied,
Substituting back in , rearranging this expression gives the following for the covariation of the correlated Brownian motions,
In particular, independent Brownian motions have zero covariation.
Existence of Quadratic Variations
It remains to prove that the quadratic variations and covariations defined by Theorem 1 do indeed exist, and then that the integration by parts formula is satisfied. In fact, it is easier to first define to be the unique process satisfying equation (6), and then show that the limit stated by Theorem 1 holds. It follows directly from this definition that
is a cadlag adapted process. Taking
then it is enough to prove the limit
. The corresponding limit for the covariation will follow from the polarization identities
and
.
The method of proof will be to express as a stochastic integral, so that the dominated convergence theorem can be used to show that this tends to zero as the mesh of the partition vanishes. Fixing a time
and partition
, as in equation (3), the square of the change in
across an interval,
, can be rearranged as
The last term on the right can be expressed as the integral of with respect to
between the limits
and
. Also substituting in the integration by parts formula (7) for the first two terms,
If we sum this expression over , then the integrand in the final term becomes
giving the following expression for the quadratic variation along a partition
| (9) |
Now, let be a sequence of such partitions whose mesh
goes to zero as
. It is clear from the left continuity of
that
. Furthermore,
, which is locally bounded. Then, the dominated convergence theorem says that
, converging ucp and in the semimartingale topology. Putting this into (9) gives
as required.
This proves the result in the case where everywhere for all
. The final thing to do is to generalize to the case where
only goes to zero in probability. However, in that case it is possible to pass to a subsequence
satisfying
for all
. The Borel-Cantelli lemma guarantees that
almost everywhere for all
. The above proof then shows that
, converging ucp and in the semimartingale topology. Then, by this same argument, every subsequence of
itself has a subsequence converging to
. As the cadlag processes under the ucp and semimartingale topologies is a metric space, this is enough to guarantee convergence of the original sequence.
Dear George,
do the partitions need to be nested in order to define the quadratic variation. I still remember having done one exercise in Peres’ book on Brownian motion that showed that some weird stuffs can happen for non-nested partitions. On the other hand, it seems like you do not need this assumption here, and I remember that the first time I learned my stochastic analysis it was not needed as well. I guess I am missing something, somewhere …
Many thanks,
Alekk
No, the partitions do not need to be nested.
You can show that, if they are nested and fixed times are used ( rather than stopping times) then, for Brownian motion, you get almost sure convergence to the quadratic variation. This follows from martingale convergence. That probably what the exercise was referring to.
The weaker notion of convergence in probability is used in my post. This works for all semimartingales and does not need nested partitions.
It is something a little bit more annoying: it can be shown (see in Peres’s book, http://www.stat.berkeley.edu/~peres/) that they exist (necessarily non-nested) sequences of deterministic partitions such that almost surely,
such that almost surely, ![\limsup [B]^{P_N}_t = +\infty](https://s0.wp.com/latex.php?latex=%5Climsup+%5BB%5D%5E%7BP_N%7D_t+%3D+%2B%5Cinfty&bg=ffffff&fg=000000&s=0&c=20201002) . Indeed, this is not a contradiction with the convergence in probability, but I just find it quite deranging.
. Indeed, this is not a contradiction with the convergence in probability, but I just find it quite deranging.
I just read again this passage of Peres’ book (exercice 1.13): there even exist random sequences of partitions such that
such that ![\lim [B]^{P_N}_t = +\infty](https://s0.wp.com/latex.php?latex=%5Clim+%5BB%5D%5E%7BP_N%7D_t+%3D+%2B%5Cinfty&bg=ffffff&fg=000000&s=0&c=20201002) : this time this is even more annoying, isnt it ? (I have not done myself this exercice with random partitions, though)
: this time this is even more annoying, isnt it ? (I have not done myself this exercice with random partitions, though)
Well, whether you find that annoying depends on your point of view, but I don’t think it should be too surprising. Convergence in probability does not usually tell you much about convergence at individual points of the probability space.
E.g., take any sequence of IID random variables with unbounded support (normal, say). Even though it will be bounded in probability, their limsup will be infinite. Then, multiplying them by a sequence of real numbers converging to zero slowly enough gives a sequence of rvs tending to zero in probability but whose limsup is infinite, and there will be a (random) subsequence which goes to infinity.
Also, given a sample path of BM, with probability one there will be a sequence of nested partitions along which its QV is infinite. There will also be nested partitions along which its QV is zero (as for any continuous function) and any number in between. So, you can construct nested random partitions partitions along which the QV is any nonnegative number you like.
Similar things happen for other situations where you have convergence in probability. E.g., there are sequences of predictable integrands converging uniformly to zero such that
converging uniformly to zero such that 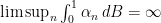 . The dominated convergence theorem gives convergence in probability, but not almost sure convergence (although almost sure convergence does occur for monotone sequences of integrands).
. The dominated convergence theorem gives convergence in probability, but not almost sure convergence (although almost sure convergence does occur for monotone sequences of integrands).
If a sequence converges in probability quickly enough, then Borel-Cantelli gives almost sure convergence. Otherwise you need something special, such as martingale convergence.
thank you very much for these explanations!
I always thought of the concept of quadratic variation as something very stable and robust, and this is why I was a little bit annoyed about these kind of pathologies. Also, from a practical point of view, this might be a little bit annoying: if we observe an unknown stochastic process, a diffusion say, and want to do some kind of inference on the volatility function, we might want to have good properties for the quadratic variation function. In general, I think that this is a difficult (and important) statistical problem.
Dear George,
I was wondering how to interpret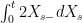 ,
, 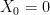 . The explicit solution when
. The explicit solution when 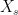 is geometric Brownian motion or a jump-diffusion (Levy process), is
is geometric Brownian motion or a jump-diffusion (Levy process), is  . But I do not have an intuitive understanding of why this is so (and, therefore, why it isn’t for alternative processes).
. But I do not have an intuitive understanding of why this is so (and, therefore, why it isn’t for alternative processes).
Thanks!,
Nikunj
Hi,
I’m not sure quite what you are asking. The explicit solution is![X_t^2-[X]_t](https://s0.wp.com/latex.php?latex=X_t%5E2-%5BX%5D_t&bg=ffffff&fg=000000&s=0&c=20201002) . That’s stochastic, and not the same thing as
. That’s stochastic, and not the same thing as  .
.
Maybe I can help if you clarify your question? (and apologies for being slow to respond.)
My bad; I forgot to add in the expectation. I meant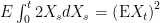 . So, for example, suppose
. So, for example, suppose 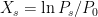 where
where  with
with 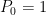 . Then,
. Then,  .
.
ah, ok. That is equivalent to![\mathbb{E}\left[ [X]_t\right] = {\rm Var}(X_t)](https://s0.wp.com/latex.php?latex=%5Cmathbb%7BE%7D%5Cleft%5B+%5BX%5D_t%5Cright%5D+%3D+%7B%5Crm+Var%7D%28X_t%29&bg=ffffff&fg=000000&s=0&c=20201002) . This holds for any square integrable martingale (it’s just the Ito Isometry). It also holds for any process of the form
. This holds for any square integrable martingale (it’s just the Ito Isometry). It also holds for any process of the form 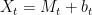 where M is a square integrable martingale and
where M is a square integrable martingale and 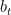 is a deterministic FV process (which does not affect either the variance or quadratic variation). This includes Brownian motion plus drift and square integrable Lévy processes. It’s a consequence of ‘orthogonality’ of increments, so that
is a deterministic FV process (which does not affect either the variance or quadratic variation). This includes Brownian motion plus drift and square integrable Lévy processes. It’s a consequence of ‘orthogonality’ of increments, so that
for times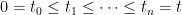 . Letting the mesh
. Letting the mesh 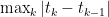 go to zero (and assuming nice integrability properties), the right hand side will converge to
go to zero (and assuming nice integrability properties), the right hand side will converge to ![\mathbb{E}\left[ [X]_t\right]](https://s0.wp.com/latex.php?latex=%5Cmathbb%7BE%7D%5Cleft%5B+%5BX%5D_t%5Cright%5D&bg=ffffff&fg=000000&s=0&c=20201002) .
.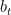 is stochastic will not satisfy this. E.g.,
is stochastic will not satisfy this. E.g., 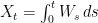 has zero quadratic variation, but nonzero variance.
has zero quadratic variation, but nonzero variance.
Processes where the drift term
Thank you very much! This is really helpful!
🙂
I have a question on something that has really been troubling me about quadratic variations…if you could help, it would really be awesome..
It says on http://planetmath.org/encyclopedia/QuadraticVariation.html that ” it can be shown if any continuous deterministic process has a well defined quadratic variation along all partitions, then it is zero.” A brownian motion almost surely has quadratic variation t. However, suppose we generate a Brownian motion path and take it as fixed. Now, it is a deterministic path and should have zero quadratic variation??
More specifically, suppose we have the process d X_t = X_t d B_t + X_t d Z_t, where B_t and Z_t are independent Brownian motions. Suppose we condition X_t in [0,T] on a particular path B_{[0,T]}. So the path of B_t is now deterministic. Then, would we still use Ito for d f(X_t) (which follows from quadratic variation)??
would d f(X_t) = f_x(X_t) dX_t + .5 X_t^2 f_xx(X_t) dt or d f(X_t) = f_x(X_t) dX_t + X_t^2 f_xx(X_t) dt ??
My intuition tells me it should be the former since why would we apply Ito to a (now) deterministic process B_t ?
Thank you very much in advance for your insight into this..
Actually, individual sample paths of Brownian motion do not have well defined quadratic variation. At least, not if you define the quadratic variation along arbitrary partitions. You can (almost-surely) find a sequence partitions with mesh going to zero on which the quadratic variation tends to zero, and other partitions on which the quadratic variation tends to infinity. See, also, the discussion with Alekk above.
thank you. that’s quite interesting.
For applications this seems quite strange. one often poses a model and we then try to fit it to past data. the model may include a brownian motion (or similar path) which we assume we have observed completely from past data. (for instance, in the simple example I’ve given above, suppose B_t is observed and we wish to find the conditional distribution of the function f(X_t) given its observed path.)
If the quadratic variation is not well-defined for any sample path (and we assume the historical data comes from such a sample path), how can we even approach such a problem?
thank you again for any insight!
The quadratic variation can be defined on each sample path if you use a fixed sequence of partitions, independently of the values on the particular path. Although, it still might not converge on individual paths if the mesh doesnt go to zero fast enough. Practically, that doesn’t matter. Pick your partition, sample the process at those times and calculate the quadratic variation with the necessary error bounds. It is only if you were going to choose the partition in a way depending on the values that the process samples take that it would be possible to go wrong.
Thank you. Your answers have been very helpful as I try to understand this.
So, are you saying, even if I choose a deterministic partition a priori, it is not guaranteed that the quadratic variation for a single path of a Brownian motion will converge as i refine my mesh?
Also, since B_t is a realization of a single path, the integral f(X_t) = […..] + f'(X_t) d B_t is not well-defined (where X_t = Z_t + B_t and I observe B_t, as earlier). It is not well-defined in the mean square sense and obviously not the lebesgue-stieljes sense (even if the function f has nice properties, I believe). I realize there has been some theoretical work on pathwise construction of such integrals. However, more importantly, how do we know a standard euler method converges to the correct integral?
These questions seems to be brushed under the rug in the literature since; for instance, the Zakai equation also integrates against a single observed path of a Brownian motion, but I see no mention of this technical issue in the literature (they appear to just use Euler).
Hi. Sorry about being a bit slow to respond. Its a bit late to be writing a long response right now, but I’ll just mention that convergence of the (approximations to) the integral is no problem, as long as your partitions use deterministic times or stopping times, and you are happy with convergence in probability. For Euler schemes, convergence in probability is what you probably want (or maybe L2 convergence or similar for technical reasons). On individual paths, you are not guaranteed convergence if your sequence of partitions does not go to zero fast enough. However, any single fine enough partition will give you a tight confidence interval for the integral, if you want to do it in a precise way.
If we are to get d where X Y and Z are continuous semimartingales, what would that evaluate to? Also, how would one go about proving Doob’s L2 inequality?
Hi George,
I have been reading your blog for a while as it has been a great source for me to understand stochastic calculus. I have the following question regarding quadratic covariation:
Let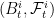 ,
,  be two Brownian motions. Suppose the filtration
be two Brownian motions. Suppose the filtration 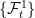 is contained in the filtration
is contained in the filtration  . As a result,
. As a result,  may not be adapted to
may not be adapted to 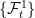 , while
, while 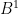 may not be a semi-martingale with respect to
may not be a semi-martingale with respect to  .
.
1. Is there a way to define (or make sense of ) the quadratic covariation process![[B^1,B^2]](https://s0.wp.com/latex.php?latex=%5BB%5E1%2CB%5E2%5D&bg=ffffff&fg=000000&s=0&c=20201002) ?
?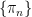 with
with  , does the Riemann sum
, does the Riemann sum 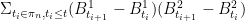 converge in an sense?(say in probability,etc)
converge in an sense?(say in probability,etc)
2. Given a sequence of refining partitions
I have looked up things like Young integral and Follmer’s pathwise integral and none of those seem to be applicable in this case. Any help and suggestion would be greatly appreciated!
Hi.
You can always define the quadratic covariation using a sequence of partitions. It is not guaranteed to exist – I think I could come up with counterexamples for which it fails to converge in your situation.
Hi George,
Thank you for your reply. It’s not clear to me how a counterexample can be constructed. In most cases, the limit fails to exist due to its blowing up to infinity. In my case, the sequence of Riemann sums are already bounded in L2. If you have any idea on disproving convergence, please kindly let me know!
best,
Ryan
Hi.
I don’t have time to post a detailed construction right now, but there do exist examples where the correlation is -1 on some timescales and +1 on others. Computed along a sequence of partitions, the covariation will oscillate between +t and -t.
I agree that one can construct two Brownian motions such that, almost surely, the approximating sums converge to different limits along different sequence of partitions (I tried the Levy Ciesielski construction which seemed to work out nicely). However, the natural filtrations of those two Brownian motions does not necessarily satisfy the condition that one must be contained in the other, and I am not sure how to get away with this issue. Could you point me to some reference on the construction you mentioned? Thank you so much!
I did think of a construction satisfying your properties, in response to your question. I should get time to post it later this weekend.
That’s great! I’m looking forward to seeing your construction!
Hey. Apologies that I have not had chance yet to post the construction. It is a bit tricky, and I wasn’t 100% sure about it at first. I have given it a bit more thought though, and I think my construction works fine. I’ll try and post it later tonight.
No hurry! I’m also working on something similar. Please let me know once you have your construction posted.
Hi Geroge,
Sorry to bother you again. I am just wondering if you have made use of any sort of ergodic theory or theory of stationary sequence in your construction. I have tried many things and none of them worked, so I am hoping you can provide me some idea and insight into your construction. Thanks in advance!
Ryan
Sorry, haven’t had much time to write it out. But, the idea is to use Brownian bridge constructions on smaller and smaller timescales for which the correlations between the processes alternates between 1 and -1. Essentially, given an initial choice for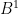 , use a small rescaling of time such that on some fine enough partition,
, use a small rescaling of time such that on some fine enough partition, 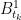 is
is  -measurable. Then interpolate between these times by linear interpolation plus a Browian bridge with correlation 1 or -1 with
-measurable. Then interpolate between these times by linear interpolation plus a Browian bridge with correlation 1 or -1 with  . This is a bit tricky, but I think it all works out and, taking the limit of such constructions gives a Brownian motion with correlation alternating between 1 and -1 in different timescales.
. This is a bit tricky, but I think it all works out and, taking the limit of such constructions gives a Brownian motion with correlation alternating between 1 and -1 in different timescales.
Thanks for your reply! I am assuming that you fix and
and 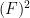 and construct
and construct 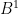 . It seems to be crucial to require
. It seems to be crucial to require 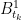 to be measurable with respect to
to be measurable with respect to  at each step to make sure the interpolation term is adpated. However, when you add in the Brownian bridge term, it seems that the property of
at each step to make sure the interpolation term is adpated. However, when you add in the Brownian bridge term, it seems that the property of 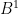 being measurable one mesh size ahead w.r.t.
being measurable one mesh size ahead w.r.t.  is destroyed. Is my understanding correct or am I missing something?
is destroyed. Is my understanding correct or am I missing something?
Ryan
You are correct, which is the point of the rescaling of time. i.e., before doing the Brownian Bridge interpolation, replace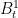 by
by 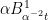 for
for  slightly greater than one.
slightly greater than one.
Hi George,
I think i understand most of your idea of construction, but still cannot get it correctly. I guess I will wait and see if you have time to post it. Thank you very much for your help!
Dear George,
Very sorry to bother you again as I still have some questions…
1.My understanding of the Brownian bridge construction is that at every step of the construction, the approximating process, when evaluated at the mesh points, has the same joint distribution as a Brownian motion. This seems to fail after the time rescaling. Based on my understanding, to go from step n to n+1, you first replace $B_t^{1,n}$ by $\alpha B_{t/\alpha^2}^{1,n}$, then set $B_t^{1,n+1}=\frac{t-t_k^n}{t_{k+1}^n-t_k^n}B_{t_{k+1}^n}^{1,n}+\frac{t_{k+1}^n-t}{t_{k+1}^n-t_k^n}B_{t_k^n}^{1,n}+(-1)^n (t_{k+1}^n-t)\int_{t_k^n}^t \frac{\,dB_u^2}{t_{k+1}^n-u}$ for t \in [t_k^n,t_{k+1}^n]$. A time-rescaling seems to change the joint distribution of such process.
2. I guess you have to start the construction somewhere away from time 0? Since rescaling of time by $\alpha$ close to 1 will not give you the desired “one mesh size ahead” measurability” at the first few mesh point.
3. As you apply time-rescaling at each step of the construction, it’s not obvious if one can write down a formula describing the relation between the limiting process and the approximating process when evaluated at corresponding partition points.(as oppose to the standard case where the values are fixed from step to step) I am therefore wondering how do you compute covariation along different timescales and show they go to different limit.
Again very sorry to bother you as this problem has puzzled me for quite a while and i really want to have a definite answer of it.
Thanks!
Hey, sorry, I really have not had much time to respond here. I do intend to answer this though.
– Start by fixing the Brownian motion on a (fixed) filtered probability space
on a (fixed) filtered probability space ![(\Omega,\mathcal{F},\{\mathcal{F}^2_t\}_{t\in[0,1]},\mathbb{P})](https://s0.wp.com/latex.php?latex=%28%5COmega%2C%5Cmathcal%7BF%7D%2C%5C%7B%5Cmathcal%7BF%7D%5E2_t%5C%7D_%7Bt%5Cin%5B0%2C1%5D%7D%2C%5Cmathbb%7BP%7D%29&bg=ffffff&fg=000000&s=0&c=20201002) . I will drop the superscript 2 just to make it easier to type. I’m also restricting the time index to [0,1] for simplicity.
. I will drop the superscript 2 just to make it easier to type. I’m also restricting the time index to [0,1] for simplicity.
– We need to construct a process W, which is a Brownian motion under its natural filtration, and is adapted (but not a BM) w.r.t. the filtration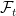 .
.
If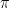 is a partition of [0,1], write
is a partition of [0,1], write ![[B,W]^\pi](https://s0.wp.com/latex.php?latex=%5BB%2CW%5D%5E%5Cpi&bg=ffffff&fg=000000&s=0&c=20201002) for the covariation computed along
for the covariation computed along 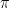 . For the required counterexample, we want a sequence of partitions with mesh going to zero but where $[B,W]^\pi$ does not converge in probability.
. For the required counterexample, we want a sequence of partitions with mesh going to zero but where $[B,W]^\pi$ does not converge in probability.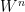 , adapted to the filtration, such that, for each n,
, adapted to the filtration, such that, for each n,  can be chosen as close as we like to
can be chosen as close as we like to 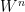 (ucp) and with
(ucp) and with ![[B,W^{n+1}]_1=(-1)^n](https://s0.wp.com/latex.php?latex=%5BB%2CW%5E%7Bn%2B1%7D%5D_1%3D%28-1%29%5En&bg=ffffff&fg=000000&s=0&c=20201002) .
.
To do this, it is enough to have a method of constructing sequences of Brownian motions
If we can do this, then simultaneously choose partitions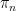 and
and 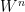 as follows. Once
as follows. Once 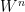 is chosen,
is chosen, close enough to
close enough to 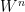 to guarantee convergence of the sequence. e.g.,
to guarantee convergence of the sequence. e.g., 
![[B,W^{n+1}]^{\pi_k}](https://s0.wp.com/latex.php?latex=%5BB%2CW%5E%7Bn%2B1%7D%5D%5E%7B%5Cpi_k%7D&bg=ffffff&fg=000000&s=0&c=20201002) is very close to
is very close to ![[B,W^{n}]^{\pi_k}](https://s0.wp.com/latex.php?latex=%5BB%2CW%5E%7Bn%7D%5D%5E%7B%5Cpi_k%7D&bg=ffffff&fg=000000&s=0&c=20201002) for each
for each  . For example,
. For example, ![\mathbb{P}(\sup_t\lvert [B,W^{n+1}]^{\pi_k}-[B,W^{n}]^{\pi_k}\rvert > 2^{-n}) < 2^{-n}](https://s0.wp.com/latex.php?latex=%5Cmathbb%7BP%7D%28%5Csup_t%5Clvert+%5BB%2CW%5E%7Bn%2B1%7D%5D%5E%7B%5Cpi_k%7D-%5BB%2CW%5E%7Bn%7D%5D%5E%7B%5Cpi_k%7D%5Crvert+%3E+2%5E%7B-n%7D%29+%3C+2%5E%7B-n%7D&bg=ffffff&fg=000000&s=0&c=20201002) .
. so that
so that ![[B,W^{n+1}]^{\pi_{n+1}}](https://s0.wp.com/latex.php?latex=%5BB%2CW%5E%7Bn%2B1%7D%5D%5E%7B%5Cpi_%7Bn%2B1%7D%7D&bg=ffffff&fg=000000&s=0&c=20201002) is very close to
is very close to 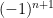 . For example,
. For example, ![\mathbb{P}(\lvert[B,W^{n+1}]^{\pi_{n+1}}-(-1)^{n+1}\rvert > 2^{-n})< 2^{-n}. Then, it can be seen that](https://s0.wp.com/latex.php?latex=%5Cmathbb%7BP%7D%28%5Clvert%5BB%2CW%5E%7Bn%2B1%7D%5D%5E%7B%5Cpi_%7Bn%2B1%7D%7D-%28-1%29%5E%7Bn%2B1%7D%5Crvert+%3E+2%5E%7B-n%7D%29%3C+2%5E%7B-n%7D.++Then%2C+it+can+be+seen+that+&bg=ffffff&fg=000000&s=0&c=20201002) latex W^n$ converges everywhere almost surely to a Brownian motion W. Furthermore,
latex W^n$ converges everywhere almost surely to a Brownian motion W. Furthermore, ![(-1)^n[B,W]^{\pi_n}\to1](https://s0.wp.com/latex.php?latex=%28-1%29%5En%5BB%2CW%5D%5E%7B%5Cpi_n%7D%5Cto1&bg=ffffff&fg=000000&s=0&c=20201002) , so
, so ![[B,W]^{\pi_n}](https://s0.wp.com/latex.php?latex=%5BB%2CW%5D%5E%7B%5Cpi_n%7D&bg=ffffff&fg=000000&s=0&c=20201002) does not converge.
does not converge.
– choose
– choose it close enough that
– choose the partition
Dear George,
Thanks for your reply! I am a little bit confused on where the Brownian bridge construction(time rescaling+brownian bridge interpolation) comes into play in your construction. I am also very curious on how to choose the partition. In my attempt the partition is fixed apriori to be the dyadic rationals.
I have posted my question on MO:
http://mathoverflow.net/questions/254788/brownian-motions-under-different-filtrations-quadratic-covariation-convergence
You can share your solution there whenever you have some time. Thanks!
Ryan
Hi. I’ve seen your mathoverflow post, and will get to it when I have some time. Unfortunately, I can’t at the moment, but will get back to it soon.
Dear George,
I am not sure if you remember, that six months ago, I consulted you this question on Brownian Motions under different filtrations and existence of quadratic covariation as limit of Riemann sum. You mentioned that you had a counter-example where the Riemann sum diverged.
This problem has remained a mystery to me until now. I have so far not been able to construct an counterexample, nor can I prove convergence. I am therefore wondering if you will have time to revisit this problem.
Thanks in advance!
Best,
Ryan
Hi George,
first: thank you a lot for this blog, it’s an amazing source for stochastic calculus!
I am seriously confused about one point where your definition of the quadratic variation seems to be different from the one in Protter’s book. Apparently Protter defines the quadratic variation (and quadratic covariation) such that there is an additional term X_0 Y_0. Do you know what I mean? Otherwise I can provide more details… But there are a lot of instances there where it really makes a difference if one integrates over [0, t] or (0, t], for example… Is it possible that there are different conventions in the literature?
Hi Jakob,
Yes, this is just a matter of convention about what you do at time 0. Obviously any statement using one convention can be converted to an equivalent statement using the other. I’ll have to check for explicit definitions in the literature, but I am sure both are used. Similar issues occur in many places, such as the integral (as you mentioned), the definition of predictable processes and stopping times, the Doob-Meyer decomposition, dual projections, etc. In a way, you could consider extending your processes to negative times, by either being constant equal to their time 0 values, or equal to 0 there. I.e, do you consider your processes to have a jump at time zero or not? I made a choice (no jump at time 0) and stuck to it throughout these notes.
Thanks
George
I checked a few sources. Rogers & Williams (Diffusions, Markov Processes, and Martingales), Metivier (Semimartingales), Jacod & Shiryaev (Limit Theorems for stochastic processes), Kallenberg (Foundations of Modern Probability) all have quadratic variation starting from 0. Protter is the outlier here, but either convention is fine IMO as long as you are consistent.
In Theorem 3, the integrals make sense due to “consequence” to Lemma 5 in “Properties of…”. However, when one reads your notes non-linearly, this reduction is quite hard to find! It seems that a hyperlink would help a lot… Thanks!
I was a bit confused about your derivation of (2). I think maybe you meant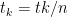 ?
?
I did mean that, thanks!
Fixed.
I am not sure how you get the inequality in the final proof. For instance if you have
in the final proof. For instance if you have  then
then  , which may not be zero. How do you explicitly get this inequality for all
, which may not be zero. How do you explicitly get this inequality for all  ?
?
Well spotted! This was a typo really, I should have used the running maximum of X rather than X itself. I fixed it.