The Stochastic Fubini Theorem

Fubini’s theorem states that, subject to precise conditions, it is possible to switch the order of integration when computing double integrals. In the theory of stochastic calculus, we also encounter double integrals and would like to be able to commute their order. However, since these can involve stochastic integration rather than the usual deterministic case, the classical results are not always applicable. To help with such cases, we could do with a new stochastic version of Fubini’s theorem. Here, I will consider the situation where one integral is of the standard kind with respect to a finite measure, and the other is stochastic. To start, recall the classical Fubini theorem.

Theorem 1 (Fubini) Let ${(E,\mathcal E,\mu)}$ and ${(F,\mathcal F,\nu)}$ be finite measure spaces, and ${f\colon E\times F\rightarrow{\mathbb R}}$ be a bounded ${\mathcal E\otimes\mathcal F}$ -measurable function. Then,

$\displaystyle y\mapsto\int f(x,y)d\mu(x)$

is ${\mathcal F}$ -measurable,

$\displaystyle x\mapsto\int f(x,y)d\nu(y)$

is ${\mathcal E}$ -measurable, and,

$\displaystyle \int\int f(x,y)d\mu(x)d\nu(y)=\int\int f(x,y)d\nu(x)d\mu(y).$ (1)

Continue reading “The Stochastic Fubini Theorem” →

Purely Discontinuous Semimartingales

As stated by the Bichteler-Dellacherie theorem, all semimartingales can be decomposed as the sum of a local martingale and an FV process. However, as the terms are only determined up to the addition of an FV local martingale, this decomposition is not unique. In the case of continuous semimartingales, we do obtain uniqueness, by requiring the terms in the decomposition to also be continuous. Furthermore, the decomposition into continuous terms is preserved by stochastic integration. Looking at non-continuous processes, there does exist a unique decomposition into local martingale and predictable FV processes, so long as we impose the slight restriction that the semimartingale is locally integrable.

In this post, I look at another decomposition which holds for all semimartingales and, moreover, is uniquely determined. This is the decomposition into continuous local martingale and purely discontinuous terms which, as we will see, is preserved by the stochastic integral. This is distinct from each of the decompositions mentioned above, except for the case of continuous semimartingales, in which case it coincides with the sum of continuous local martingale and FV components. Before proving the decomposition, I will start by describing the class of purely discontinuous semimartingales which, although they need not have finite variation, do have many of the properties of FV processes. In fact, they comprise precisely of the closure of the set of FV processes under the semimartingale topology. The terminology can be a bit confusing, and it should be noted that purely discontinuous processes need not actually have any discontinuities. For example, all continuous FV processes are purely discontinuous. For this reason, the term `quadratic pure jump semimartingale’ is sometimes used instead, referring to the fact that their quadratic variation is a pure jump process. Recall that quadratic variations and covariations can be written as the sum of continuous and pure jump parts,

$\displaystyle \setlength\arraycolsep{2pt} \begin{array}{rl} \displaystyle [X]_t&\displaystyle=[X]^c_t+\sum_{s\le t}(\Delta X_s)^2,\smallskip\\ \displaystyle [X,Y]_t&\displaystyle=[X,Y]^c_t+\sum_{s\le t}\Delta X_s\Delta Y_s. \end{array}$

(1)

The statement that the quadratic variation is a pure jump process is equivalent to saying that its continuous part, ${[X]^c}$ , is zero. As the only difference between the generalized Ito formula for semimartingales and for FV processes is in the terms involving continuous parts of the quadratic variations and covariations, purely discontinuous semimartingales behave much like FV processes under changes of variables and integration by parts. Yet another characterisation of purely discontinuous semimartingales is as sums of purely discontinuous local martingales — which were studied in the previous post — and of FV processes.

Rather than starting by choosing one specific property to use as the definition, I prove the equivalence of various statements, any of which can be taken to define the purely discontinuous semimartingales.

Theorem 1 For a semimartingale X, the following are equivalent.

${[X]^c=0}$ .

${[X,Y]^c=0}$ for all semimartingales Y.

${[X,Y]=0}$ for all continuous semimartingales Y.

${[X,M]=0}$ for all continuous local martingales M.

${X=M+V}$ for a purely discontinuous local martingale M and FV process V.

there exists a sequence ${\{X^n\}_{n=1,2,\ldots}}$ of FV processes such that ${X^n\rightarrow X}$ in the semimartingale topology.

Continue reading “Purely Discontinuous Semimartingales” →

The Burkholder-Davis-Gundy Inequality

The Burkholder-Davis-Gundy inequality is a remarkable result relating the maximum of a local martingale with its quadratic variation. Recall that [X] denotes the quadratic variation of a process X, and ${X^*_t\equiv\sup_{s\le t}\vert X_s\vert}$ is its maximum process.

Theorem 1 (Burkholder-Davis-Gundy) For any ${1\le p<\infty}$ there exist positive constants ${c_p,C_p}$ such that, for all local martingales X with ${X_0=0}$ and stopping times ${\tau}$ , the following inequality holds.

$\displaystyle c_p{\mathbb E}\left[ [X]^{p/2}_\tau\right]\le{\mathbb E}\left[(X^*_\tau)^p\right]\le C_p{\mathbb E}\left[ [X]^{p/2}_\tau\right].$ (1)

Furthermore, for continuous local martingales, this statement holds for all ${0<p<\infty}$ .

A proof of this result is given below. For ${p\ge 1}$ , the theorem can also be stated as follows. The set of all cadlag martingales X starting from zero for which ${{\mathbb E}[(X^*_\infty)^p]}$ is finite is a vector space, and the BDG inequality states that the norms ${X\mapsto\Vert X^*_\infty\Vert_p={\mathbb E}[(X^*_\infty)^p]^{1/p}}$ and ${X\mapsto\Vert[X]^{1/2}_\infty\Vert_p}$ are equivalent.

The special case p=2 is the easiest to handle, and we have previously seen that the BDG inequality does indeed hold in this case with constants ${c_2=1}$ , ${C_2=4}$ . The significance of Theorem 1, then, is that this extends to all ${p\ge1}$ .

One reason why the BDG inequality is useful in the theory of stochastic integration is as follows. Whereas the behaviour of the maximum of a stochastic integral is difficult to describe, the quadratic variation satisfies the simple identity ${\left[\int\xi\,dX\right]=\int\xi^2\,d[X]}$ . Recall, also, that stochastic integration preserves the local martingale property. Stochastic integration does not preserve the martingale property. In general, integration with respect to a martingale only results in a local martingale, even for bounded integrands. In many cases, however, stochastic integrals are indeed proper martingales. The Ito isometry shows that this is true for square integrable martingales, and the BDG inequality allows us to extend the result to all ${L^p}$ -integrable martingales, for ${p> 1}$ .

Theorem 2 Let X be a cadlag ${L^p}$ -integrable martingale for some ${1<p<\infty}$ , so that ${{\mathbb E}[\vert X_t\vert^p]<\infty}$ for each t. Then, for any bounded predictable process ${\xi}$ , ${Y\equiv\int\xi\,dX}$ is also an ${L^p}$ -integrable martingale.

Continue reading “The Burkholder-Davis-Gundy Inequality” →

Continuous Local Martingales

Continuous local martingales are a particularly well behaved subset of the class of all local martingales, and the results of the previous two posts become much simpler in this case. First, the continuous local martingale property is always preserved by stochastic integration.

Theorem 1 If X is a continuous local martingale and ${\xi}$ is X-integrable, then ${\int\xi\,dX}$ is a continuous local martingale.

Proof: As X is continuous, ${Y\equiv\int\xi\,dX}$ will also be continuous and, therefore, locally bounded. Then, by preservation of the local martingale property, Y is a local martingale. ⬜

Next, the quadratic variation of a continuous local martingale X provides us with a necessary and sufficient condition for X-integrability.

Theorem 2 Let X be a continuous local martingale. Then, a predictable process ${\xi}$ is X-integrable if and only if

$\displaystyle \int_0^t\xi^2\,d[X]<\infty$

for all ${t>0}$ .

Continue reading “Continuous Local Martingales” →

Quadratic Variations and the Ito Isometry

As local martingales are semimartingales, they have a well-defined quadratic variation. These satisfy several useful and well known properties, such as the Ito isometry, which are the subject of this post. First, the covariation [X,Y] allows the product XY of local martingales to be decomposed into local martingale and FV terms. Consider, for example, a standard Brownian motion B. This has quadratic variation ${[B]_t=t}$ and it is easily checked that ${B^2_t-t}$ is a martingale.

Lemma 1 If X and Y are local martingales then XY-[X,Y] is a local martingale.

In particular, ${X^2-[X]}$ is a local martingale for all local martingales X.

Proof: Integration by parts gives

$\displaystyle XY-[X,Y] = X_0Y_0+\int X_-\,dY+\int Y_-\,dX$

which, by preservation of the local martingale property, is a local martingale. ⬜

Continue reading “Quadratic Variations and the Ito Isometry” →

Preservation of the Local Martingale Property

Now that it has been shown that stochastic integration can be performed with respect to any local martingale, we can move on to the following important result. Stochastic integration preserves the local martingale property. At least, this is true under very mild hypotheses. That the martingale property is preserved under integration of bounded elementary processes is straightforward. The generalization to predictable integrands can be achieved using a limiting argument. It is necessary, however, to restrict to locally bounded integrands and, for the sake of generality, I start with local sub and supermartingales.

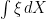Theorem 1 Let X be a local submartingale (resp., local supermartingale) and ${\xi}$ be a nonnegative and locally bounded predictable process. Then, ${\int\xi\,dX}$ is a local submartingale (resp., local supermartingale).

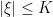Proof: We only need to consider the case where X is a local submartingale, as the result will also follow for supermartingales by applying to -X. By localization, we may suppose that ${\xi}$ is uniformly bounded and that X is a proper submartingale. So, ${\vert\xi\vert\le K}$ for some constant K. 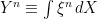Then, as previously shown there exists a sequence of elementary predictable processes ${\vert\xi^n\vert\le K}$ such that ${Y^n\equiv\int\xi^n\,dX}$ converges to 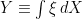${Y\equiv\int\xi\,dX}$ in the semimartingale topology and, hence, converges ucp. We may replace 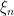${\xi_n}$ by ${\xi_n\vee0}$ if necessary so that, being nonnegative elementary integrals of a submartingale, ${Y^n}$ will be submartingales. 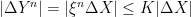Also, ${\vert\Delta Y^n\vert=\vert\xi^n\Delta X\vert\le K\vert\Delta X\vert}$ . Recall that a cadlag adapted process X is locally integrable if and only its jump process ${\Delta X}$ is locally integrable, and all local submartingales are locally integrable. So,

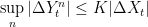
$\displaystyle \sup_n\vert\Delta Y^n_t\vert\le K\vert\Delta X_t\vert$

is locally integrable. Then, by ucp convergence for local submartingales, Y will satisfy the local submartingale property. ⬜

For local martingales, applying this result to ${\pm X}$ gives,

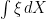Theorem 2 Let X be a local martingale and ${\xi}$ be a locally bounded predictable process. Then, ${\int\xi\,dX}$ is a local martingale.

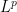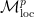This result can immediately be extended to the class of local ${L^p}$ -integrable martingales, denoted by ${\mathcal{M}^p_{\rm loc}}$ .

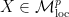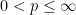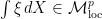Corollary 3 Let ${X\in\mathcal{M}^p_{\rm loc}}$ for some ${0< p\le\infty}$ and ${\xi}$ be a locally bounded predictable process. Then, ${\int\xi\,dX\in\mathcal{M}^p_{\rm loc}}$ .

Continue reading “Preservation of the Local Martingale Property” →

Martingales are Integrators

A major foundational result in stochastic calculus is that integration can be performed with respect to any local martingale. In these notes, a semimartingale was defined to be a cadlag adapted process with respect to which a stochastic integral exists satisfying some simple desired properties. Namely, the integral must agree with the explicit formula for elementary integrands and satisfy bounded convergence in probability. Then, the existence of integrals with respect to local martingales can be stated as follows.

Theorem 1 Every local martingale is a semimartingale.

This result can be combined directly with the fact that FV processes are semimartingales.

Corollary 2 Every process of the form X=M+V for a local martingale M and FV process V is a semimartingale.

Working from the classical definition of semimartingales as sums of local martingales and FV processes, the statements of Theorem 1 and Corollary 2 would be tautologies. Then, the aim of this post is to show that stochastic integration is well defined for all classical semimartingales. Put in another way, Corollary 2 is equivalent to the statement that classical semimartingales satisfy the semimartingale definition used in these notes. The converse statement will be proven in a later post on the Bichteler-Dellacherie theorem, so the two semimartingale definitions do indeed agree.

Continue reading “Martingales are Integrators” →

Semimartingale Completeness

A sequence of stochastic processes, ${X^n}$ , is said to converge to a process X under the semimartingale topology, as n goes to infinity, if the following conditions are met. First, ${X^n_0}$ should tend to ${X_0}$ in probability. Also, for every sequence ${\xi^n}$ of elementary predictable processes with ${\vert\xi^n\vert\le 1}$ ,

$\displaystyle \int_0^t\xi^n\,dX^n-\int_0^t\xi^n\,dX\rightarrow 0$

in probability for all times t. For short, this will be denoted by ${X^n\xrightarrow{\rm sm}X}$ .

The semimartingale topology is particularly well suited to the class of semimartingales, and to stochastic integration. Previously, it was shown that the cadlag and adapted processes are complete under semimartingale convergence. In this post, it will be shown that the set of semimartingales is also complete. That is, if a sequence ${X^n}$ of semimartingales converge to a limit X under the semimartingale topology, then X is also a semimartingale.

Theorem 1 The space of semimartingales is complete under the semimartingale topology.

The same is true of the space of stochastic integrals defined with respect to any given semimartingale. In fact, for a semimartingale X, the set of all processes which can be expressed as a stochastic integral ${\int\xi\,dX}$ can be characterized as follows; it is precisely the closure, under the semimartingale topology, of the set of elementary integrals of X. This result was originally due to Memin, using a rather different proof to the one given here. The method used in this post only relies on the elementary properties of stochastic integrals, such as the dominated convergence theorem.

Theorem 2 Let X be a semimartingale. Then, a process Y is of the form ${Y=\int\xi\,dX}$ for some ${\xi\in L^1(X)}$ if and only if there is a sequence ${\xi^n}$ of bounded elementary processes with ${\int\xi^n\,dX\xrightarrow{\rm sm}Y}$ .

Writing S for the set of processes of the form ${\int\xi\,dX}$ for bounded elementary ${\xi}$ , and ${\bar S}$ for its closure under the semimartingale topology, the statement of the theorem is equivalent to

$\displaystyle \bar S=\left\{\int\xi\,dX\colon \xi\in L^1(X)\right\}.$

(1)

Continue reading “Semimartingale Completeness” →

Further Properties of the Stochastic Integral

We move on to properties of stochastic integration which, while being fairly elementary, are rather difficult to prove directly from the definitions.

First, recall that for a semimartingale X, the X-integrable processes ${L^1(X)}$ were defined to be predictable processes ${\xi}$ which are ‘good dominators’. That is, if ${\xi^n}$ are bounded predictable processes with ${\vert\xi^n\vert\le\vert\xi\vert}$ and ${\xi^n\rightarrow 0}$ pointwise, then ${\int_0^t\xi^n\,dX}$ tends to zero in probability. This definition is a bit messy. Fortunately, the following result gives a much cleaner characterization of X-integrability.

Theorem 1 Let X be a semimartingale. Then, a predictable process ${\xi}$ is X-integrable if and only if the set

$\displaystyle \left\{\int_0^t\zeta\,dX\colon\zeta\in{\rm b}\mathcal{P},\vert\zeta\vert\le\vert\xi\vert\right\}$ (1)

is bounded in probability for each ${t\ge 0}$ .

Continue reading “Further Properties of the Stochastic Integral” →

Existence of the Stochastic Integral 2 – Vector Valued Measures

The construction of the stochastic integral given in the previous post made use of a result showing that certain linear maps can be extended to vector valued measures. This result, Theorem 1 below, was separated out from the main argument in the construction of the integral, as it only involves pure measure theory and no stochastic calculus. For completeness of these notes, I provide a proof of this now.

Given a measurable space ${(E,\mathcal{E})}$ , ${{\rm b}\mathcal{E}}$ denotes the bounded ${\mathcal{E}}$ -measurable functions ${E\rightarrow{\mathbb R}}$ . For a topological vector space V, the term V-valued measure refers to linear maps ${\mu\colon{\rm b}\mathcal{E}\rightarrow V}$ satisfying the following bounded convergence property; if a sequence ${\alpha_n\in{\rm b}\mathcal{E}}$ (n=1,2,…) is uniformly bounded, so that ${\vert\alpha_n\vert\le K}$ for a constant K, and converges pointwise to a limit ${\alpha}$ , then ${\mu(\alpha_n)\rightarrow\mu(\alpha)}$ in V.

This differs slightly from the definition of V-valued measures as set functions ${\mu\colon\mathcal{E}\rightarrow V}$ satisfying countable additivity. However, any such set function also defines an integral ${\mu(\alpha)\equiv\int\alpha\,d\mu}$ satisfying bounded convergence and, conversely, any linear map ${\mu\colon{\rm b}\mathcal{E}\rightarrow V}$ satisfying bounded convergence defines a countably additive set function ${\mu(A)\equiv \mu(1_A)}$ . So, these definitions are essentially the same, but for the purposes of these notes it is more useful to represent V-valued measures in terms of their integrals rather than the values on measurable sets.

In the following, a subalgebra of ${{\rm b}\mathcal{E}}$ is a subset closed under linear combinations and pointwise multiplication, and containing the constant functions.

Theorem 1 Let ${(E,\mathcal{E})}$ be a measurable space, ${\mathcal{A}}$ be a subalgebra of ${{\rm b}\mathcal{E}}$ generating ${\mathcal{E}}$ , and V be a complete vector space. Then, a linear map ${\mu\colon\mathcal{A}\rightarrow V}$ extends to a V-valued measure on ${(E,\mathcal{E})}$ if and only if it satisfies the following properties for sequences ${\alpha_n\in\mathcal{A}}$ .

If ${\alpha_n\downarrow 0}$ then ${\mu(\alpha_n)\rightarrow 0}$ .

If ${\sum_n\vert\alpha_n\vert\le 1}$ , then ${\mu(\alpha_n)\rightarrow 0}$ .

Continue reading “Existence of the Stochastic Integral 2 – Vector Valued Measures” →

	Anonymous on About
	Anonymous on About
	Anonymous on The Stochastic Integral
	Anonymous on Bessel Processes
	Anonymous on Bessel Processes
	Stat Prof on Pathwise Regularity of Optiona…
	Yang Chu on Spitzer’s Formula
	Anonymous on About
	Anonymous on Continuous Processes with Inde…
	Anonymous on Continuous Processes with Inde…