Quadratic Variations and the Ito Isometry

As local martingales are semimartingales, they have a well-defined quadratic variation. These satisfy several useful and well known properties, such as the Ito isometry, which are the subject of this post. First, the covariation [X,Y] allows the product XY of local martingales to be decomposed into local martingale and FV terms. Consider, for example, a standard Brownian motion B. This has quadratic variation ${[B]_t=t}$ and it is easily checked that ${B^2_t-t}$ is a martingale.

Lemma 1 If X and Y are local martingales then XY-[X,Y] is a local martingale.

In particular, ${X^2-[X]}$ is a local martingale for all local martingales X.

Proof: Integration by parts gives

$\displaystyle XY-[X,Y] = X_0Y_0+\int X_-\,dY+\int Y_-\,dX$

which, by preservation of the local martingale property, is a local martingale. ⬜

For square integrable martingales, it is possible to drop the `local’ from the statement above. That is, ${X^2-[X]}$ will be a proper martingale. Before proving this, the following simple inequality will be useful. This is actually a special case of the much more general Burkholder-Davis-Gundy inequalities, which will be covered in a later post. Recall that ${X^*_t\equiv\sup_{s\le t}\vert X_s\vert}$ denotes the maximum process of X.

Lemma 2 Let X be a local martingale with ${X_0=0}$ . Then,

$\displaystyle {\mathbb E}\left[[X]_t\right]\le{\mathbb E}\left[(X^*_t)^2\right]\le 4{\mathbb E}\left[[X]_t\right].$ (1)

Proof: By Lemma 1 there exist stopping times ${\tau_n\uparrow\infty}$ such that the stopped processes ${(X^2-[X])^{\tau_n}}$ and ${X^{\tau_n}}$ are martingales. So, ${{\mathbb E}[[X]_{t\wedge\tau_n}]={\mathbb E}[X_{t\wedge\tau_n}^2]}$ . Also, ${{\mathbb E}[(X^*_{t\wedge\tau_n})^2]\le 4{\mathbb E}[X^2_{t\wedge\tau_n}]}$ by Doob’s inequality, giving

$\displaystyle {\mathbb E}\left[[X]_{t\wedge\tau_n}\right]\le{\mathbb E}\left[(X^*_{t\wedge\tau_n})^2\right]\le 4{\mathbb E}\left[X_{t\wedge\tau_n}^2\right]=4{\mathbb E}\left[[X]_{t\wedge\tau_n}\right].$

Letting n increase to infinity and applying monotone convergence gives (1). ⬜

With the aid of this inequality, we can now prove that for square integrable martingales, ${X^2-[X]}$ will be a proper martingale. In fact, we obtain a necessary and sufficient condition for any local martingale to be a square integrable martingale.

Lemma 3 A local martingale X is a square integrable martingale if and only if ${{\mathbb E}[X_0^2]<\infty}$ and [X] is integrable, in which case ${X^2-[X]}$ is a martingale.

Proof: Replacing X by ${X-X_0}$ , we may suppose that ${X_0=0}$ . If [X] is integrable then Lemma 2 gives ${{\mathbb E}[(X^*_t)^2]<\infty}$ , so ${X^2_t-[X]_t}$ is a local martingale (by Lemma 1) and dominated by the integrable random variable ${(X^*_T)^2+[X]_T}$ (for ${t\le T}$ ). Hence, it is a proper martingale. Conversely, suppose that X is a square integrable martingale. Then, Doobs inequality shows that ${{\mathbb E}[(X^*_t)^2]\le 4{\mathbb E}[X_t^2]}$ is finite and, by Lemma 2, [X] is integrable. ⬜

In one direction, the above lemma generalizes in the obvious way to products of square integrable martingales.

Lemma 4 Let X and Y be cadlag square integrable martingales. Then, [X,Y] has integrable variation over any bounded time interval, and XY-[X,Y] is a martingale.

Proof: By the polarization identity, ${[X,Y]=([X+Y]-[X-Y])/4}$ . So, [X,Y] has variation bounded by ${([X+Y]_t+[X-Y]_t)/4}$ over any interval [0,t] which, by Lemma 2, is integrable. Then

$\displaystyle XY-[X,Y] = \left((X+Y)^2-[X+Y]\right)/4 - \left((X-Y)^2-[X-Y]\right)/4$

is a martingale, again using Lemma 2. ⬜

Recall that quadratic variations of stochastic integrals satisfy the following fundamental identity

$\displaystyle \left[\int\xi\,dX\right]=\int\xi^2\,d[X].$

Putting this together with the results above gives the Ito Isometry. In the following theorem, the random variable ${\int_0^\infty\xi\,dX}$ has zero mean, by the martingale property, and (2) gives a simple expression for the variance. Historically, the Ito isometry was first established for a Brownian motion B in which case it reads,

$\displaystyle {\mathbb E}\left[\left(\int_0^\infty\xi\,dB\right)^2\right]={\mathbb E}\left[\int_0^\infty\xi^2_t\,dt\right].$

Equation (2) represents an extension to more general local martingales.

Theorem 5 (Ito Isometry) Let X be a local martingale and ${\xi}$ be a predictable process such that ${\int_0^\infty\xi^2\,d[X]}$ has finite expectation. Then, ${\xi}$ is X-integrable, ${M\equiv\int\xi\,dX}$ is an ${L^2}$ -bounded martingale and

$\displaystyle {\mathbb E}\left[\left(\int_0^\infty\xi\,dX\right)^2\right] = {\mathbb E}\left[\int_0^\infty\xi^2\,d[X]\right].$ (2)

By martingale convergence, the limit ${M_\infty\equiv\lim_{t\rightarrow\infty}M_t}$ of the ${L^2}$ -bounded martingale M exists almost surely. So, there is no problem with integrating up to infinity in (2). Also, replacing ${\xi}$ by ${1_{(0,\tau]}\xi}$ for any stopping time ${\tau}$ shows that (2) still holds if instead we integrate up to an arbitrary stopping time.

Proof: Let us first assume that ${\xi}$ is X-integrable and set ${M=\int\xi\,dX}$ . Then, ${[M]=\int\xi^2\,d[X]}$ is integrable. So ${(\Delta M)^2=\Delta[M]}$ is locally integrable and, therefore, M is locally square integrable. By preservation of the local martingale property, M is a local martingale. By (1),

$\displaystyle {\mathbb E}\left[(M^*_\infty)^2\right]\le 4{\mathbb E}\left[[M]_\infty\right]<\infty$

so M is a uniformly ${L^2}$ -bounded martingale and Lemma 3 says that ${M^2-[M]}$ is a martingale giving,

$\displaystyle \setlength\arraycolsep{2pt} \begin{array}{rl} \displaystyle{\mathbb E}\left[M^2_\infty\right]&\displaystyle=\lim_{t\rightarrow\infty}{\mathbb E}\left[M^2_t\right]=\lim_{t\rightarrow\infty}{\mathbb E}\left[[M]_t\right]\smallskip\\ &\displaystyle={\mathbb E}\left[[M]_\infty\right]={\mathbb E}\left[\int_0^\infty\xi^2\,d[X]\right]. \end{array}$

as required.

Now, suppose that ${\xi}$ is any predictable process such that ${U\equiv\int_0^\infty\xi^2\,d[X]}$ is integrable. It just needs to be shown that if ${\vert\xi^n\vert\le\vert\xi\vert}$ is a sequence of bounded predictable processes tending to zero then ${\int_0^t\xi^n\,dX}$ tends to zero in probability, so that ${\xi}$ is X-integrable. However, by the above argument,

$\displaystyle {\mathbb E}\left[\left(\int_0^t\xi^n\,dX\right)^2\right]={\mathbb E}\left[\int_0^t(\xi^n)^2\,d[X]\right]$

By dominated convergence for Lebesgue-Stieltjes integration, ${\int_0^t(\xi^n)^2\,d[X]}$ tends to zero, and is dominated by U. Then dominated convergence for sequences of random variables says that ${{\mathbb E}[\int_0^t(\xi^n)^2\,d[X]]\rightarrow 0}$ , so ${\int_0^t\xi^n\,dX}$ tends to zero in ${L^2}$ and, therefore, also in probability. ⬜

More generally, the Ito isometry can be used to express the covariance between two stochastic integrals.

Theorem 6 Let X, Y be local martingales and ${\alpha,\beta}$ be predictable processes such that ${\int_0^\infty\alpha^2\,d[X]}$ and ${\int_0^\infty\beta^2\,d[Y]}$ are integrable. Then, ${\alpha,\beta}$ are respectively X-integrable and Y-integrable, ${\int\alpha\beta\,d[X,Y]}$ has integrable variation and,

$\displaystyle {\mathbb E}\left[\int_0^\infty\alpha\,dX\int_0^\infty\beta\,dY\right] = {\mathbb E}\left[\int_0^\infty\alpha\beta\,d[X,Y]\right].$ (3)

Proof: Theorem 5 says that ${\alpha}$ is X-integrable, ${\beta}$ is Y integrable and ${M\equiv\int\alpha\,dX}$ , ${N\equiv\int\beta\,dY}$ are ${L^2}$ -bounded martingales. The Kunita-Watanabe inequality shows that the variation of ${[M,N]=\int\alpha\beta\,d[X,Y]}$ is bounded by

$\displaystyle \int_0^\infty\,\vert d[M,N]\vert\le\sqrt{\int_0^\infty\alpha^2\,d[X]\int_0^\infty\beta^2\,d[Y]},$

which is integrable. Furthermore, by Lemma 4, ${MN-[M,N]}$ is a martingale and

$\displaystyle {\mathbb E}[M_\infty N_\infty]=\lim_{t\rightarrow\infty}{\mathbb E}[M_tN_t]=\lim_{t\rightarrow\infty}{\mathbb E}\left[[M,N]_t\right]={\mathbb E}\left[[M,N]_\infty\right]$

giving (3). ⬜

We now show that for any local martingale X and predictable process ${\xi}$ , local integrability of ${\int\xi^2\,d[X]}$ is sufficient to guarantee that ${\xi}$ is X-integrable. In fact, it is enough that ${(\int\xi^2\,d[X])^{1/2}}$ is locally integrable, which is a weaker condition, but the proof of that will have to wait until we have covered the Burkholder-Davis-Gundy inequalities.

Lemma 7 For any local martingale X and predictable process ${\xi}$ , the following are equivalent.

${\xi}$ is X-integrable and ${\int\xi\,dX\in\mathcal{M}^2_{\rm loc}}$ .

${\int\xi^2\,d[X]}$ is locally integrable.

Proof: Suppose that the first property is satisfied. Then, ${M=\int\xi\,dX}$ is locally square integrable. So, ${\Delta [M]=(\Delta M)^2}$ is locally integrable showing that ${[M]=\int\xi^2\,d[X]}$ is locally integrable.

Conversely, suppose that 2 is satisfied. Then, there are stopping times ${\tau_n\uparrow\infty}$ such that ${\int_0^{\tau_n}\xi^2\,d[X]}$ have finite expectation. So Theorem 5 says that ${1_{(0,\tau_n]}\xi}$ are X-integrable. As X-integrability is a local property, this shows that ${\xi}$ is X-integrable and, by preservation of the local martingale property, ${M=\int\xi\,dX}$ is a local martingale. Finally, ${(\Delta M)^2=\Delta[M]}$ is locally integrable, so ${M\in\mathcal{M}^2_{\rm loc}}$ . ⬜

It is not true that, for a local martingale X and predictable process ${\xi}$ , finiteness of ${\int\xi^2\,d[X]}$ at all times implies that ${\xi}$ is X-integrable. Consider the following counter-example. Let ${\tau}$ be an exponentially distributed random variable, so ${{\mathbb P}(\tau>t)=\exp(-t)}$ , and set ${X_t=1_{\{t\ge\tau\}}-t\wedge\tau}$ . This is a martingale under its natural filtration ${\{\mathcal{F}_t\}_{t\ge 0}}$ , and its quadratic variation is ${[X]_t=1_{\{t\ge\tau\}}}$ . If ${\xi_t=t^{-1}}$ then ${\int_0^t\xi^2\,d[X]=1_{\{t\ge \tau\}}\tau^{-2}}$ is finite. However, ${\xi}$ cannot be X-integrable, because, that would lead to

$\displaystyle \int_t^\tau\xi\,dX = \tau^{-1}-\int_t^\tau s^{-1}\,ds = \tau^{-1}-\log(\tau/t)$

whenever ${\tau\ge t}$ , which diverges as t decreases to zero.

It is true on the other hand, that finiteness of ${\int_0^t\xi^2\,d[X]}$ implies X-integrability for continuous local martingales, since continuous processes are locally bounded and Lemma 7 can be applied.

Finally, note that Lemma 1 can be strengthened to uniquely determine the covariation of local martingales. In fact, this is sometimes used as the initial definition of quadratic covariations.

Lemma 8 Let X, Y be local martingales. Then, [X,Y] is the unique FV process starting at 0 and satisfying the following.

XY-[X,Y] is a local martingale.

${\Delta [X,Y]=\Delta X\Delta Y}$ .

Proof: That [X,Y] satisfies property 1 is given by Lemma 1, and 2 is a basic property of the covariation. Conversely, suppose that V is any other FV process starting at zero and satisfying properties 1 and 2. Then ${W\equiv [X,Y]-V}$ will be a continuous local martingale. As it is a continuous FV process, W will have zero quadratic variation. So Lemma 3 says that ${W^2}$ is a martingale, giving ${{\mathbb E}[W_t^2]=0}$ , and V=[X,Y]. ⬜

7 thoughts on “Quadratic Variations and the Ito Isometry”

Alex says:

1 May 11 at 3:45 PM

Dear Almost Sure,
thank you very much for your notes. I have a question. If we consider the Ito’s Isometry for the Brownian Motion then we will have expected value of squared stochastic integral is equal to the expected value of the integral of the squared function. Is the latter integral in the Riemann or Lebesgue sense?
Thank you.
Sincerely,
Alex.

1. George Lowther says:
  
  2 May 11 at 12:57 AM
  
  The latter integral is in the Lebesgue sense — which is equivalent to the Riemann sense if the paths of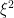 $\xi^2$ are Riemann integrable (but that is not a requirement).
  
Alex says:

12 October 11 at 5:50 PM

Dear Almost Sure,
I was reading your notes on stochastic calculus and I was wondering if there is an expression for the Riemann integral (with respect to t) of a Poisson Process or Compound Poisson Process? What is this integral equal to?
Is it also true (by Fubini Theorem) that the expectation of this integral is equal to the integral of the expectation?
Thank you.
Sincerely,
Alex.

Ilya Zakharevich says:

26 March 21 at 5:45 AM

You write:

> “which, by preservation of the local martingale property, “…

In fact, this link does not seem to help here: the assumptions there are too strict. Moreover, here too (as I wrote in a different place already) a reference to “consequence” to Lemma 5 in “Properties of…” would be quite helpful!

1. George Lowther says:
  
  26 March 21 at 1:20 PM
  
  On your first comment, this does help. X- and Y- are locally bounded, so the assumptions in the link are fine. Maybe there is confusion over the term ‘locally bounded’? All left-continuous adapted processes with right limits are locally bounded. See Localization. Or, maybe the notation X- for the left limits of the cadlag process X is the source of misunderstanding, but I use this throughout my notes.
  
  1. Ilya Zakharevich says:
    
    17 April 21 at 3:48 AM
    
    You wrote:
    > “See Localization.”
    This was indeed a very keen remark! Well, almost!
    
    I think you wanted to (essentially) refer to the argument in the proof of Lemma 13 (https://almostsuremath.com/2009/12/23/localization/#scn_local_lem13), correct?
    
    it was indeed what I have been missing. On the other hand, Google can find NO OTHER PLACE in your notes where you refer to this lemma, or provide the link from your reply. Given that a lot of people are going to read your notes non-linearly, IMO giving more cross-references would be VERY helpful!
    
    > “this does help.”
    
    — but only when one is fluent with the notions and/or when one is reading your notes IN ORDER… Given that your notes are SO GREAT even when reads them “in random order” (as in “after googling”), a few extra crosslinks would make the reading yet MORE GREAT ;–) !!! Thanks!
    
Anonymous says:

28 November 21 at 5:52 PM

Dear almost sure,

I was looking for some theorem regarding the product of two Ito integrals with different differentials, but could not find it on the book of Shreve. I think it should look like theorem 6, but may I ask where I can find this theorem? (on which book?) And would you like to recommend me some books except for the one by Shreve?

	Anonymous on About
	Anonymous on About
	Anonymous on The Stochastic Integral
	Anonymous on Bessel Processes
	Anonymous on Bessel Processes
	Stat Prof on Pathwise Regularity of Optiona…
	Yang Chu on Spitzer’s Formula
	Anonymous on About
	Anonymous on Continuous Processes with Inde…
	Anonymous on Continuous Processes with Inde…

Quadratic Variations and the Ito Isometry

Published by George Lowther

7 thoughts on “Quadratic Variations and the Ito Isometry”

Leave a comment Cancel reply

Related

Published by George Lowther

7 thoughts on “Quadratic Variations and the Ito Isometry”

Leave a comment Cancel reply