Existence of the Stochastic Integral 2 – Vector Valued Measures

The construction of the stochastic integral given in the previous post made use of a result showing that certain linear maps can be extended to vector valued measures. This result, Theorem 1 below, was separated out from the main argument in the construction of the integral, as it only involves pure measure theory and no stochastic calculus. For completeness of these notes, I provide a proof of this now.

Given a measurable space ${(E,\mathcal{E})}$ , ${{\rm b}\mathcal{E}}$ denotes the bounded ${\mathcal{E}}$ -measurable functions ${E\rightarrow{\mathbb R}}$ . For a topological vector space V, the term V-valued measure refers to linear maps ${\mu\colon{\rm b}\mathcal{E}\rightarrow V}$ satisfying the following bounded convergence property; if a sequence ${\alpha_n\in{\rm b}\mathcal{E}}$ (n=1,2,…) is uniformly bounded, so that ${\vert\alpha_n\vert\le K}$ for a constant K, and converges pointwise to a limit ${\alpha}$ , then ${\mu(\alpha_n)\rightarrow\mu(\alpha)}$ in V.

This differs slightly from the definition of V-valued measures as set functions ${\mu\colon\mathcal{E}\rightarrow V}$ satisfying countable additivity. However, any such set function also defines an integral ${\mu(\alpha)\equiv\int\alpha\,d\mu}$ satisfying bounded convergence and, conversely, any linear map ${\mu\colon{\rm b}\mathcal{E}\rightarrow V}$ satisfying bounded convergence defines a countably additive set function ${\mu(A)\equiv \mu(1_A)}$ . So, these definitions are essentially the same, but for the purposes of these notes it is more useful to represent V-valued measures in terms of their integrals rather than the values on measurable sets.

In the following, a subalgebra of ${{\rm b}\mathcal{E}}$ is a subset closed under linear combinations and pointwise multiplication, and containing the constant functions.

Theorem 1 Let ${(E,\mathcal{E})}$ be a measurable space, ${\mathcal{A}}$ be a subalgebra of ${{\rm b}\mathcal{E}}$ generating ${\mathcal{E}}$ , and V be a complete vector space. Then, a linear map ${\mu\colon\mathcal{A}\rightarrow V}$ extends to a V-valued measure on ${(E,\mathcal{E})}$ if and only if it satisfies the following properties for sequences ${\alpha_n\in\mathcal{A}}$ .

If ${\alpha_n\downarrow 0}$ then ${\mu(\alpha_n)\rightarrow 0}$ .

If ${\sum_n\vert\alpha_n\vert\le 1}$ , then ${\mu(\alpha_n)\rightarrow 0}$ .

The conditions stated are necessary for the existence of an extension to a V-valued measure because, in both cases, ${\alpha_n}$ is a uniformly bounded sequence converging to 0. Note the similarity of this result to Carathéodory’s extension theorem for standard (real-valued) measures. Suppose that ${\mathcal{A}}$ are linear combinations of indicator functions 1_A for A in some subset ${\mathcal{E}_0\subseteq\mathcal{E}}$ which is closed under finite intersections and under complements. Then, setting ${\mu(A)\equiv\mu(1_A)}$ , the conditions of the theorem are equivalent to the requirement that ${\mu(A_n)\rightarrow 0}$ whenever ${A_n\in\mathcal{E}_0}$ are either pairwise disjoint or decreasing to the empty set.

The construction of the stochastic integral only made use of the special case where ${(E,\mathcal{E})=({\mathbb R}_+\times\Omega,\mathcal{P})}$ is the predictable sigma algebra, ${V=L^0(\Omega,\mathcal{F},{\mathbb P})}$ is the space of random variables (up to almost sure equivalence) under convergence in probability, and ${\mathcal{A}}$ is the set of uniformly bounded continuous and adapted processes. However, it is not much more difficult to prove Theorem 1 in full generality, which we do here.

First, if ${\alpha_n\in{\rm b}\mathcal{E}}$ satisfy ${\vert \alpha_n\vert\le 2^{-n}}$ then ${\sum_n\vert\alpha_n\vert\le 1}$ so that, by the second condition of the theorem, ${\mu(\alpha_n)\rightarrow 0}$ . It follows that ${\mu}$ is continuous under the topology of uniform convergence on ${{\rm b}\mathcal{E}}$ and, by continuous linear extensions, extends uniquely to a continuous linear function from the closure ${\mathcal{A^*}}$ of ${\mathcal{A}}$ under uniform convergence. As ${\mathcal{A^*}}$ is an algebra, ${p(\alpha)\in\mathcal{A^*}}$ for every polynomial p and ${\alpha\in\mathcal{A^*}}$ . The Stone-Weierstrass theorem states that continuous functions on a bounded interval can be uniformly approximated by polynomials, so ${f(\alpha)\in\mathcal{A^*}}$ for all continuous functions ${f\colon{\mathbb R}\rightarrow{\mathbb R}}$ and ${\alpha\in\mathcal{A^*}}$ . Furthermore, this extension of ${\mu}$ still satisfies the conditions of the theorem. If ${\alpha_n\in\mathcal{A^*}}$ , then choose ${\beta_n\in\mathcal{A}}$ with ${\vert\alpha_n-\beta_n\vert\le 2^{-n}}$ . If ${\alpha_n\downarrow 0}$ then ${\beta_n+2^{2-n}\in\mathcal{A}}$ will also be decreasing to zero, giving ${\mu(\beta_n)\rightarrow 0}$ . Alternatively, if ${\sum_n\vert\alpha_n\vert\le 1}$ then ${\sum_n\vert\beta_n\vert\le 2}$ , again giving ${\mu(\beta_n)\rightarrow 0}$ . In either case, ${\mu(\alpha_n)=\mu(\beta_n)+\mu(\alpha_n-\beta_n)}$ tends to zero as required. So, by passing to the closure ${\mathcal{A^*}}$ if necessary, it may be assumed that ${\mathcal{A}}$ is closed under uniform convergence.

Throughout the remainder of this post, it is assumed that ${\mathcal{A}}$ is closed under uniform convergence. So, ${f(\alpha)\in\mathcal{A}}$ for continuous functions ${f\colon{\mathbb R}\rightarrow{\mathbb R}}$ and ${\alpha\in\mathcal{A}}$ . In particular, we make use of the fact that the absolute value ${\vert\alpha\vert}$ of any ${\alpha\in\mathcal{A}}$ is itself in ${\mathcal{A}}$ .

The proof I give here is close to the construction of the stochastic integral given by Bichteler in Stochastic Integration and L^p-Theory of Semimartingales and in his book, `Stochastic Integration with Jumps’. The idea is to define a semimetric D^* on the bounded measurable functions, referred to by Bichteler as the Daniell mean. Once it is shown that ${\mu}$ is continuous under this metric, a continuous linear extension to the whole of ${{\rm b}\mathcal{E}}$ can be used. Let us suppose that the topology on V is given by a translation invariant metric ${(u,v)\mapsto D(u-v)}$ . This is indeed true in the construction of the stochastic integral, where ${V=L^0(\Omega,\mathcal{F},{\mathbb P})}$ and ${D(U)\equiv{\mathbb E}[\vert U\vert\wedge 1]}$ generates the topology of convergence in probability. Generalizing to arbitrary complete vector spaces is straightforward, as demonstrated in the subsection below. By the standard metric properties, D must satisfy ${D(u+v)\le D(u)+D(v)}$ and ${D(-u)=D(u)}$ for all u,v in V. Furthermore, replacing D(v) by min(D(v),1) if required, we suppose that D is bounded.

For any ${\alpha\in\mathcal{A}}$ , define

$\displaystyle D^0(\alpha)\equiv\sup\left\{D(\mu(\beta))\colon\beta\in\mathcal{A},\vert\beta\vert\le\vert\alpha\vert\right\}$

Then, define ${D^*\colon{\rm b}\mathcal{E}\rightarrow{\mathbb R}_+}$ by

$\displaystyle D^*(\alpha)\equiv\inf\left\{\sum_{n=1}^\infty D^0(\alpha_n)\colon \{\alpha_n\}_{n\in{\mathbb N}}\in\mathcal{A}{\rm\ and\ }\vert\alpha\vert\le\sum_{n=1}^\infty \vert\alpha_n\vert\right\}.$

(1)

Although I have used a slightly different definition, this is the quantity referred to as the Daniell mean by Bichteler. In fact, D^* and D⁰ will agree on ${\mathcal{A}}$ , as we show in a moment. Countable subadditivity follows from this definition in a straightforward way, as given by the following lemma. In particular, the triangle inequality ${D^*(\alpha+\beta)\le D^*(\alpha)+D^*(\beta)}$ is satisfied, so D^* defines a translation invariant semimetric on ${{\rm b}\mathcal{E}}$ .

Lemma 2 Suppose that ${\alpha,\{\alpha_n\}_{n\in{\mathbb N}}\in{\rm b}\mathcal{E}}$ satisfy ${\vert\alpha\vert\le\sum_n\vert\alpha_n\vert}$ . Then,

$\displaystyle D^*(\alpha)\le\sum_{n=1}^\infty D^*(\alpha_n).$ (2)

Proof: Using (1), for any ${\epsilon>0}$ there exist ${\alpha_{n,m}\in\mathcal{A}}$ satisfying ${\sum_m\vert\alpha_{n,m}\vert\ge\vert\alpha_n\vert}$ and

$\displaystyle \sum_{m=1}^\infty D^0(\alpha_{n,m})\le D^*(\alpha_n)+2^{-n}\epsilon.$

As ${\vert\alpha\vert\le\sum_{n,m}\vert\alpha_{n,m}\vert}$ ,

$\displaystyle D^*(\alpha)\le\sum_{n,m}D^0(\alpha_{n,m})\le\sum_n(D^*(\alpha_n)+2^{-n}\epsilon)=\sum_nD^*(\alpha_n)+\epsilon.$

As ${\epsilon>0}$ was arbitrary, (2) follows. ⬜

Let us also show that D^* and D⁰ agree on ${\mathcal{A}}$ . In particular, this gives ${D(\mu(\alpha))\le D^*(\alpha)}$ , so that ${\mu}$ is continuous with respect to the semimetric D^*.

Lemma 3 For any ${\alpha\in\mathcal{A}}$ ,

$\displaystyle D^*(\alpha)=D^0(\alpha)=\sup\left\{D(\mu(\beta))\colon \beta\in\mathcal{A},\vert\beta\vert\le\vert\alpha\vert\right\}.$

Proof: Setting ${\alpha_1=\alpha}$ and ${\alpha_n=0}$ for n=2,3,… in (1) gives ${D^*(\alpha)\le D^0(\alpha)}$ , so only the reverse inequality needs to be shown.

Given any ${\beta_1,\beta_2,\gamma\in\mathcal{A}}$ with ${\vert\gamma\vert\le\vert\beta_1+\beta_2\vert}$ , setting ${\gamma_1=(\gamma\wedge\vert\beta_1\vert)\vee(-\vert\beta_1\vert)}$ and ${\gamma_2=\gamma-\gamma_1}$ gives ${\vert\gamma_1\vert\le\vert\beta_1\vert}$ and ${\vert\gamma_2\vert\le\vert\beta_2\vert}$ . So,

$\displaystyle D(\mu(\gamma))\le D(\mu(\gamma_1))+D(\mu(\gamma_2))\le D^0(\beta_1)+D^0(\beta_2).$

Taking the supremum over all ${\vert\gamma\vert\le\vert\beta_1+\beta_2\vert}$ gives the triangle inequality,

$\displaystyle D^0(\beta_1+\beta_2)\le D^0(\beta_1)+D^0(\beta_2).$

Now choose a sequence ${\alpha_n\in\mathcal{A}}$ with ${\vert\alpha\vert\le\sum_n\vert\alpha_n\vert}$ and set ${\beta_n=\sum_{k=1}^n\vert\alpha_k\vert}$ . For any ${\gamma\in\mathcal{A}}$ with ${\vert\gamma\vert\le\vert\alpha\vert}$ , set ${\gamma_n=(\gamma\wedge\beta_n)\vee(-\beta_n)}$ so that ${\vert\gamma_n\vert\le \vert\beta_n\vert}$ .

Then, ${(\gamma-\gamma_n)\vee 0}$ and ${(\gamma_n-\gamma)\vee 0}$ decrease monotonically to zero. So, by the first property of Theorem 1,

$\displaystyle \mu(\gamma)-\mu(\gamma_n)=\mu((\gamma-\gamma_n)\vee 0)-\mu((\gamma_n-\gamma)\vee 0)\rightarrow 0.$

Then, applying the triangle inequality for D⁰, we obtain the following

$\displaystyle \setlength\arraycolsep{2pt} \begin{array}{rl} \displaystyle D(\mu(\gamma)) &\displaystyle=\lim_{n\rightarrow\infty}D(\mu(\gamma_n))\le\lim_{n\rightarrow\infty}D^0(\beta_n)\smallskip\\ &\displaystyle\le \lim_{n\rightarrow\infty}\sum_{k=1}^n D^0(\alpha_k)=\sum_{n=1}^\infty D^0(\alpha_n). \end{array}$

Taking the infimum over all such ${\alpha_n}$ and applying (1) gives ${D(\mu(\gamma))\le D^*(\alpha)}$ . Then taking the supremum over ${\vert\gamma\vert\le\vert\alpha\vert}$ gives ${D^0(\alpha)\le D^*(\alpha)}$ as required. ⬜

Now, let ${\mathcal{\bar A}\subseteq{\rm b}\mathcal{E}}$ be the closure of ${\mathcal{A}}$ with respect to the topology generated by the semimetric D^*. That is, ${\alpha\in\mathcal{\bar A}}$ if and only if there is a sequence ${\alpha_n\in\mathcal{A}}$ such that ${D^*(\alpha-\alpha_n)\rightarrow 0}$ . Then, D^* satisfies monotone convergence on ${\mathcal{\bar A}}$ .

Lemma 4 Let ${\alpha_n\in\mathcal{\bar A}}$ and ${\alpha\in{\rm b}\mathcal{E}}$ be such that ${0\le\alpha_n\uparrow\alpha}$ . Then, ${\alpha\in\mathcal{\bar A}}$ and ${D^*(\alpha-\alpha_n)\rightarrow 0}$ .

Proof: First, let us show that ${D^*(\alpha_n-\alpha_m)\rightarrow 0}$ as m,n go to infinity. Choose any ${\epsilon>0}$ and ${\beta_n\in\mathcal{A}}$ with ${D^*(\beta_n-\alpha_n)<2^{-n}\epsilon}$ . Suppose that ${\alpha\le K}$ for some constant K. Replacing ${\beta_n}$ by ${(\beta_n\wedge K)\vee 0}$ if necessary, we may suppose that ${0\le\beta_n\le K}$ . Then, setting ${\gamma_n=\beta_1\vee\cdots\vee\beta_n}$ ,

$\displaystyle \setlength\arraycolsep{2pt} \begin{array}{rl} \displaystyle\gamma_n-\alpha_n &\displaystyle=\gamma_{n-1}\vee\beta_n-\alpha_n =(\gamma_{n-1}-\alpha_n)\vee(\beta_n-\alpha_n)\smallskip\\ &\displaystyle\le(\gamma_{n-1}-\alpha_{n-1})\vee(\beta_n-\alpha_n). \end{array}$

So, ${\gamma_n-\alpha_n}$ is bounded below by ${\beta_n-\alpha_n}$ and above by ${\vert\gamma_{n-1}-\alpha_{n-1}\vert+\vert\beta_n-\alpha_n\vert}$ . Applying the triangle inequality,

$\displaystyle \setlength\arraycolsep{2pt} \begin{array}{rl} \displaystyle D^*(\gamma_n-\alpha_n)&\displaystyle\le D^*(\gamma_{n-1} - \alpha_{n-1})+D^*(\beta_n-\alpha_n)\smallskip\\ &\displaystyle\le D^*(\gamma_{n-1} - \alpha_{n-1})+2^{-n}\epsilon. \end{array}$

Summing over n=2,…,m gives

$\displaystyle D^*(\gamma_m-\alpha_m)\le \epsilon.$

Now, choose any sequence ${n_k\uparrow\infty}$ . As ${0\le\gamma_n\le K}$ is increasing, ${\gamma_{n_k}-\gamma_{n_{k-1}}\in\mathcal{A}}$ has a sum bounded by K. So, any ${\tilde\gamma_k\in\mathcal{A}}$ with ${\vert\tilde\gamma_k\vert\le\vert\gamma_{n_k}-\gamma_{n_{k-1}}\vert}$ also have a sum bounded by K and, by the second condition of Theorem 1, ${\mu(\tilde\gamma_k)\rightarrow 0}$ . By Lemma 3, we can choose ${D(\mu(\tilde\gamma_k))\ge D^*(\gamma_{n_k}-\gamma_{n_{k-1}})-2^{-k}}$ , showing that ${D^*(\gamma_{n_k}-\gamma_{n_{k-1}})\rightarrow 0}$ . Since the sequence ${n_k\uparrow\infty}$ was arbitrary, this shows that ${D^*(\gamma_m-\gamma_n)\rightarrow 0}$ as m,n go to infinity. So,

$\displaystyle \limsup_{m,n\rightarrow\infty}D^*(\alpha_m-\alpha_n)\le 2\epsilon + \limsup_{m,n\rightarrow\infty}D(\gamma_m-\gamma_n)\le 2\epsilon.$

As ${\epsilon>0}$ was arbitrary, this shows that ${D^*(\alpha_m-\alpha_n)\rightarrow 0}$ as required.

Now choosing ${n_k\uparrow\infty}$ such that ${D^*(\alpha_m-\alpha_n)<2^{-k}}$ whenever ${m,n\ge n_k}$ then, for ${n\ge n_k}$ , countable subadditivity (Lemma 2) gives

$\displaystyle D^*(\alpha-\alpha_n) \le \sum_{j=k}^\infty D^*(\alpha_{n_{j+1}}-\alpha_{n_j})\le\sum_{j=k}^\infty 2^{-j}=2^{1-k},$

which goes to 0 as k increases to infinity. ⬜

Putting together the previous lemmas, it is now straightforward to show that ${\mathcal{\bar A}}$ is the whole of ${{\rm b}\mathcal{E}}$ and that D^* satisfies bounded convergence.

Lemma 5 The equality ${\mathcal{\bar A}={\rm b}\mathcal{E}}$ holds. Furthermore, suppose that ${\alpha_n\in{\rm b}\mathcal{E}}$ are uniformly bounded by some constant K, so that ${\vert\alpha_n\vert\le K}$ , and ${\alpha_n\rightarrow\alpha\in{\rm b}\mathcal{E}}$ pointwise as n goes to infinity. Then, ${D^*(\alpha-\alpha_n)\rightarrow 0}$ .

Proof: As ${\mathcal{\bar A}\subseteq{\rm b}\mathcal{E}}$ is a linear space closed under monotone limits (by Lemma 4), and contains the algebra ${\mathcal{A}}$ generating ${\mathcal{E}}$ , the monotone class theorem says that ${\mathcal{\bar A}={\rm b}\mathcal{E}}$ .

Now, suppose that ${\alpha_n\in\mathcal{A}}$ satisfy ${\vert\alpha_n\vert\le K}$ and ${\alpha_n\rightarrow\alpha}$ . The sequence ${\beta_n=\sup_{m\ge n}\vert\alpha-\alpha_m\vert}$ decreases monotonically to zero. So, ${\beta_1-\beta_m\uparrow\beta_1}$ and Lemma 4 gives ${D^*(\beta_m)\rightarrow 0}$ . Therefore,

$\displaystyle D^*(\alpha_n-\alpha)\le D^*(\beta_n)\rightarrow 0$

as required. ⬜

The extension of ${\mu}$ to a V-valued measure is finally given by a continuous linear extension, completing the proof of Theorem 1.

Lemma 6 Let V be a complete vector space, with translation invariant metric D. Then, assuming the conditions of Theorem 1, ${\mu}$ extends uniquely to a V-valued measure on ${(E,\mathcal{E})}$ .

Proof: Define the semimetric D^* on ${{\rm b}\mathcal{E}}$ as in (1). By Lemma 3, ${D(\mu(\alpha))\le D^*(\alpha)}$ . So, ${\mu}$ is D^*/D-continuous and extends uniquely to a continuous linear function ${\mu^*\colon{\rm b}\mathcal{E}\rightarrow V}$ which, by Lemma 5, satisfies the bounded convergence property. ⬜

Generalizing to arbitrary complete vector spaces

The proof of Theorem 1 can be extended to arbitrary complete vector spaces, not given by a translation invariant metric. This is not needed for the construction of the stochastic integral, but it is not difficult, and I do this now for the sake of giving a full proof of the theorem as stated. We can use the result that any vector topology is given by a collection of translation invariant semimetrics ${\{D_i\}_{i\in I}}$ . As above, replacing D_i(v) by min(D_i(v),1), we may suppose that D_i are bounded. Then, by the above argument, there is a collection ${\{D^*_i\}_{i\in I}}$ of semimetrics on ${{\rm b}\mathcal{E}}$ such that ${D_i(\mu(\alpha))\le D^*_i(\alpha)}$ for all ${\alpha\in\mathcal{A}}$ , and satisfying bounded convergence as in Lemma 5.

Then, the closure ${\mathcal{\bar A}\subseteq{\rm b}\mathcal{E}}$ of ${\mathcal{A}}$ with respect to the topology generated by ${\{D_i\}_{i\in I}}$ is a linear space closed under monotone convergence (by Lemma 4) and, by the monotone class theorem, is the whole of ${{\rm b}\mathcal{E}}$ . By continuous linear extensions, ${\mu}$ extends uniquely to a continuous linear function ${\mu^*\colon{\rm b}\mathcal{E}\rightarrow V}$ . By Lemma 5, ${\mu^*}$ satisfies bounded convergence and hence is a V-valued measure.

The statement that all vector topologies are generated by a set of translation invariant semimetrics needs some explanation. It is a standard result of functional analysis that a vector topology is given by such a semimetric if and only if it has a countable base of neighborhoods of the origin. Then, for an aribitrary vector topology ${\mathcal{T}}$ , let ${\{U_i\}_{i\in I}}$ be a base of balanced neighborhoods of the origin. For each i, by the properties of vector topologies, there is a sequence of balanced neighborhoods of the origin U_i,n such that ${U_{i,{n+1}}+U_{i,{n+1}}\subseteq U_{i,n}}$ and U_i,n=U_i. Again, by standard results of functional analysis, ${\{U_{i,n}\colon n=1,2,\ldots\}}$ generate a vector topology which will then be generated by some translation invariant semimetric D_i. The set ${\{D_i\}_{i\in I}}$ generates ${\mathcal{T}}$ as required.

3 thoughts on “Existence of the Stochastic Integral 2 – Vector Valued Measures”

kebabroyal says:

6 December 11 at 8:39 AM

Hi

Two questions, on this very interesting topic:
– What do you mean exactly by “generating $\mathcal{E}$ in Theorem 1 ?
– Where can I find a book where this theorem is stated ? This is the first time I see integration presented this way.

Regards

1. George Lowther says:
  
  7 December 11 at 2:47 AM
  
  Hi.
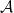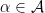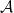  By saying that $\mathcal{A}$ generates $\mathcal{E}$ I mean that $\mathcal{E}$ is the smallest σ-algebra with respect to which every $\alpha\in\mathcal{A}$ is measurable. By the monotone class theorem, this is equivalent to $b\mathcal{E}$ being the smallest collection of functions $E\to\mathbb{R}$ containing $\mathcal{A}$ and closed under taking limits of uniformly bounded monotone sequences.
  
  I don’t have a precise reference for Theorem 1.
  The treatment of stochastic integration in this and the previous post is based very roughly on that given by Bichteler in the book Stochastic Integration with Jumps, and he has a freely downloadable version on his website. However, the way in which I arrange the proof here is largely my own, so Theorem 1 is not quoted from any other source. The main trick which I used here from Bichteler’s method is the use of the Khintchine inequality (Lemma 3 of the previous post). This guarantees that the stochastic integral satisfies the second statement of Theorem 1 above. My proof of existence of the stochastic integral is organized rather differently from Bichteler’s though. I split out the part of the construction which depends on the specific properties of the stochastic integral (in the previous post) from the part which works for arbitrary vector valued measures (Theorem 1 above).
  
  You could take a look at The Carathéodory extension theorem for vector valued measures. The main theorem quoted there is very similar to Theorem 1, except that it is stated for Banach spaces (so not L⁰) and is for actual vector measures, rather than the σ-additive linear functions here.
  
Jens says:

9 June 14 at 7:32 AM

Just as the Riemann–Stieltjes integral can be equivalently defined as a Lebesgue integral with the corresponding Lebesgue–Stieltjes measure, I am looking for similar/corresponding results for the relationship between Stochastic integrals (both Ito and Stratonovich) and Bochner Integrals (or any other integral taking values in Banach spaces). I’m also looking for results on the corresponding measure defined on the relevant Banach Spaces.

Information pertaining to Stochastic integrals with integration with respect to Brownian motion is more than welcome, but I am looking for results pertaining more to integrals with integration in respect to more general semi-martingales. Any references or results you can forward to me is greatly appreciated. Thanks.

	Harry on Filtrations and Adapted P…
	Anonymous on Analytic Sets
	Daniel on Analytic Sets
	Sid on Martingale Convergence
	northwiz on Preservation of the Local Mart…
	George Lowther on Martingale Convergence
	Sid on Martingale Convergence
	George Lowther on The Burkholder-Davis-Gundy Ine…
	George Lowther on Preservation of the Local Mart…
	northwiz on Preservation of the Local Mart…

Existence of the Stochastic Integral 2 – Vector Valued Measures

Generalizing to arbitrary complete vector spaces

Published by George Lowther

3 thoughts on “Existence of the Stochastic Integral 2 – Vector Valued Measures”

Leave a Reply Cancel reply

Generalizing to arbitrary complete vector spaces

Like this:

Related

Published by George Lowther

3 thoughts on “Existence of the Stochastic Integral 2 – Vector Valued Measures”

Leave a Reply Cancel reply