The martingale property is strong enough to ensure that, under relatively weak conditions, we are guaranteed convergence of the processes as time goes to infinity. In a previous post, I used Doob’s upcrossing inequality to show that, with probability one, discrete-time martingales will converge at infinity under the extra condition of -boundedness. Here, I consider continuous-time martingales. This is a more general situation, because it considers limits as time runs through the uncountably infinite set of positive reals instead of the countable set of positive integer times. Although these results can also be proven in a similar way by counting the upcrossings of a process, I instead show how they follow directly from the existence of cadlag modifications. We work with respect to a complete filtered probability space
.
Recall that a stochastic process is
-bounded if the set
is
-bounded. That is,
is bounded above by some finite value as
runs through the positive reals.
Theorem 1 Let
be a cadlag and
-bounded martingale (or submartingale, or supermartingale). Then, the limit
exists and is finite, with probability one.
Proof: It suffices to consider submartingales, as the martingale and supermartingale cases follow from applying the result to . So, suppose that
is a submartingale such that
is bounded above by some real number
. Define the process
by
and the filtration for
and
otherwise. Clearly
is right-continuous and is a submartingale with respect to this filtration over the range
. The idea is to use the results of the post on cadlag modifications to show that it has a cadlag version, in which case the limit
exists almost surely.
Consider an elementary process of the form
for a finite sequence of times ,
-measurable random variables
and
-measurable random variable
. If
then
. Also, let
be the first of the times satisfying
. Then, using the submartingale property for
,
So the set of expectations of elementary integrals for
is bounded by
, and it follows that
has a cadlag modification. ⬜
A particularly simple consequence of this is that nonnegative martingales and supermartingales always have well defined limits at infinity.
Corollary 2 If
is a nonnegative cadlag martingale (or supermartingale) then the limit
exists and is finite, with probability one.
Proof: The supermartingale property gives showing that
is
bounded. So the previous result applies. ⬜
For uniformly integrable random variables, the following stronger result is obtained. Recall that a process is uniformly integrable if the set of random variables
is uniformly integrable.
Theorem 3 Let
be a uniformly integrable cadlag martingale. Then, the limit
exists with probability one. Furthermore, this is the unique (up to a zero probability set) integrable and
-measurable random variable such that
for each
.
Proof: As uniformly integrable sets are -bounded, Theorem 1 shows that the limit
exists and is almost surely finite. Uniform integrability allows us to take the limit
in the equality
to obtain
. It only remains to show that this is the only integrable
-measurable random variable with this property. So, suppose that
for all
and some integrable and
-measurable
. Then
for all and
. The monotone class theorem extends this to all
from which it follows that
almost surely. ⬜
Continuous martingales
Even stronger convergence results exist for continuous martingales.
Theorem 4 Let
be a continuous martingale. Then, almost surely, one of the following is satisfied
exists and is finite.
and
. In this case, the process hits every value in
at arbitrarily large times.
In the second statement above, the property that the process hits every value at arbitrarily large times is nothing more than the intermediate value theorem applied to and
.
Consider, for example, a standard Brownian motion . The sequence
of random variables are independent with the standard normal distribution, so
cannot converge in the limit as
goes to infinity. Consequently, the second statement of Theorem 4 holds, showing that, with probability one, Brownian motion hits every real value at arbitrarily large times.
Theorem 4 follows from applying the following to both and
.
Lemma 5 Let
be a continuous submartingale. Then, almost surely, one of the following is satisfied.
exists and is finite.
.
Proof: Let be the sequence of stopping times
Then, is a nonnegative supermartingale and Corollary 2 says that it must converge at infinity. This can only happen if either
converges or if
. Letting
increase to infinity gives the result. ⬜
Although it is possible to generalize Theorem 4 to discontinuous process, it would still be necessary to put restrictions on the size of the jumps . The result does not hold for arbitrary cadlag processes. To see this, consider the following example.
Choose a sequence such that
. For example, we could take
. Then let
be a sequence of independent random variables satisfying
and
. By the Borel Cantelli lemma,
for all large
(with probability one). The process
is a martingale with respect to its natural filtration. However, with probability one, it ends up by forever oscillating up and down by unit jumps, so never converges and never diverges to infinity.
Dear George,
I’m curious as to why exactly ythe cadlag property is required for Theorem 1. The proof seems to hold without any use of it.
Thanks,
Tigran
The proof uses the fact that the constructed process Y is right-continuous and, as any two right-continuous modifications of the same process are equal (up to evanescence), Y must equal its cadlag modification and, hence, have left-limits.
So, you need right-continuity. For martingales, right-continuity is equivalent to being cadlag.
I am wondering how you get that![X_t={\mathbb E}[X_\infty\mid\mathcal{F}_t]](https://s0.wp.com/latex.php?latex=X_t%3D%7B%5Cmathbb+E%7D%5BX_%5Cinfty%5Cmid%5Cmathcal%7BF%7D_t%5D&bg=ffffff&fg=000000&s=0&c=20201002) follows from uniform convergence in the proof of theorem 3 since
follows from uniform convergence in the proof of theorem 3 since  uniformly integrable and
uniformly integrable and  does not necessarily imply
does not necessarily imply ![E[Y_t\mid\mathcal{G}]\rightarrow E[Y_\infty\mid \mathcal{G}]](https://s0.wp.com/latex.php?latex=E%5BY_t%5Cmid%5Cmathcal%7BG%7D%5D%5Crightarrow+E%5BY_%5Cinfty%5Cmid+%5Cmathcal%7BG%7D%5D&bg=ffffff&fg=000000&s=0&c=20201002) ?
?
I think it does imply![E[Y_t\mid\mathcal{G}]\rightarrow E[Y_\infty\mid \mathcal{G}]](https://s0.wp.com/latex.php?latex=E%5BY_t%5Cmid%5Cmathcal%7BG%7D%5D%5Crightarrow+E%5BY_%5Cinfty%5Cmid+%5Cmathcal%7BG%7D%5D&bg=ffffff&fg=000000&s=0&c=20201002) , with
, with  convergence.
convergence.
Dear George,
For theorem 4 and lemma 5, we require the martingale to be continuous. You have given an example of a cadlag martingale for which which inferences of the theorem 4 fails.
However, in the proof of lemma 5, where have you used the fact that submartingale is continuous? For the sequence of hitting times to be stopping times we just require right continuity(Debut theorem).
This is implicit in the statement that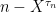 is nonnegative. If X was not continuous, it could jump right past the level n resulting in
is nonnegative. If X was not continuous, it could jump right past the level n resulting in 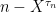 going negative.
going negative.
Actually, to be strict, I should have assumed (wlog) that X starts from 0, just to ensure that it does not start from above n [Update: I fixed the proof to address this].
Thank you for the response.
Dear George,
I recently encountered a discrete version of Theorem 4 in Exercise 8.12 of “Exercices de probabilités: Licence, master, écoles d’ingénieurs” (2016). It states:
Let $(X_n){n in mathbb{N}}$ be a martingale such that $mathbb{E}[sup{n in mathbb{N}} |X_n – X_{n-1}|] < +infty$, where $X_{-1} := 0$. Define: $A_1 := {lim_{n to +infty} X_n text{ exists and is finite}}$ $A_2 := {liminf_{n to +infty} X_n = -infty text{ and } limsup_{n to +infty} X_n = +infty}$ Then $mathbb{P}(A_1 sqcup A_2) = 1$.
I realized the condition $mathbb{E}[sup_{n in mathbb{N}} |X_n – X_{n-1}|] < +infty$ can be omitted in the continuous-time setting with continuous martingale paths, which led me to your post.
Could you provide a reference for Theorem 4? I’m interested in finding its original source.
Thank you in advance.