Special classes of processes, such as martingales, are very important to the study of stochastic calculus. In many cases, however, processes under consideration `almost’ satisfy the martingale property, but are not actually martingales. This occurs, for example, when taking limits or stochastic integrals with respect to martingales. It is necessary to generalize the martingale concept to that of local martingales. More generally, localization is a method of extending a given property to a larger class of processes. In this post I mention a few definitions and simple results concerning localization, and look more closely at local martingales in the next post.
Definition 1 Let P be a class of stochastic processes. Then, a process X is locally in P if there exists a sequence of stopping times
such that the stopped processes
are in P. The sequence
is called a localizing sequence for X (w.r.t. P).
I write for the processes locally in P. Choosing the sequence
of stopping times shows that
. A class of processes is said to be stable if
is in P whenever X is, for all stopping times
. For example, the optional stopping theorem shows that the classes of cadlag martingales, cadlag submartingales and cadlag supermartingales are all stable.
Definition 2 A process is a
- a local martingale if it is locally in the class of cadlag martingales.
- a local submartingale if it is locally in the class of cadlag submartingales.
- a local supermartingale if it is locally in the class of cadlag supermartingales.
The class of cadlag martingales is denoted by , and the class of local martingales is written as
. Furthermore, for
, a martingale X is said to be
-integrable if
is
-integrable for each time. That is
. Then,
denotes the cadlag
-integrable martingales, and
the local
-integrable and cadlag martingales.
Another property which is frequently useful in a local form is that of uniformly bounded processes. A process X is uniformly bounded if, almost surely, for all times t and some constant K.
Definition 3 A process is locally bounded if it is locally in the class of uniformly bounded processes.
As an example, all continuous adapted processes are locally bounded, with the localizing sequence . More generally, for right-continuous filtrations, this holds for left-continuous adapted processes which are almost surely bounded on every finite time interval, including all left-continuous adapted process with right limits.
A process X is integrable if is integrable at each time t. Furthermore, for any
, it is
integrable if
is
-integrable at all times. For
this means that
is finite, and for
it means that
is uniformly bounded. Unfortunately, these definitions do not give stable classes. Instead, I define local integrability as follows. Recall that, for a process X, its maximum process is
.
Definition 4 A process X is locally integrable if
is locally in the class of integrable processes.
More generally, for any, X is locally
-integrable if
is locally in the class of
-integrable processes.
Equivalently, for , the process X is locally
-integrable iff
is locally integrable. Similarly, it is locally
-integrable iff it is locally bounded. As the class of processes whose maximum process is
-integrable is stable, they behave well under localization and the definition of local integrability given above works well. Also, for nonnegative increasing processes,
, in which case it is not necessary to refer to the maximum process in the definition above. The textbook definition of local integrability is often only applied to increasing processes, and the definition I state above is a useful generalization to arbitrary processes.
Localizing a pair of properties separately is equivalent to localizing the combination of the properties. For example, is equal to the space of processes which are both a local martingale and also locally
-integrable.
Lemma 5 If P,Q are stable classes of processes then
Proof: The inclusion is trivial. Conversely, suppose that the process X is in
. Let
be localizing sequences with respect to P and Q respectively. By stability of P,
So, . Similarly,
. ⬜
Localizing a property is something which only needs to be done at most once, as repeated localization has no effect, as stated in the following result. For example, the space of processes which are locally in is just the same thing as the space of local martingales.
Lemma 6 If P is a stable vector space of processes then
.
Proof: If then there is a sequence
of stopping times such that
Then, there are sequences
of stopping times increasing to infinity as
for each fixed
, and
. Setting
gives a countable set of stopping times with
, and
by the following lemma. ⬜
Lemma 7 Let P be a stable vector space of processes. Then, a process X is locally in P if and only if there is a sequence
of stopping times with
and such that
.
Proof: If X is locally in P, then any localizing sequence satisfies the required properties. Conversely, suppose that
satisfy the required properties. Then,
are stopping times increasing to infinity. It just needs to be shown that
are in P. Using induction, suppose that this is true for a given n.
By the induction hypothesis and stability of P, each of the terms on the right hand side is in P and, as this is a vector space, so is the left hand side. Therefore, is a localizing sequence. ⬜
Local integrability
As was noted above, continuous and adapted processes are always locally bounded and, hence, locally integrable. More generally, for cadlag adapted processes, local integrability can be described in terms of the jumps of the process.
Lemma 8 For any
then a cadlag adapted process X is locally
-integrable if and only if
is locally
-integrable.
Proof: Note that is
-integrable whenever
is. Therefore,
is locally
-integrable whenever X is.
Conversely, suppose that is
-integrable. Defining the stopping times
gives
whenever , which is
integrable. Then,
is a localizing sequence showing that X is locally
-integrable. So, applying Lemma 6, X is locally
-integrable whenever
is. ⬜
The class (D) property is easily seen to be stable, and should localize nicely. However, this just leads to local integrability.
Lemma 9 For a cadlag adapted process X, the following are equivalent.
- X is locally integrable.
- X is locally of class (DL).
- X is locally of class (D).
Proof: First, if is integrable then, for each time
, the set of random variables
for stopping times
is dominated by the integrable variable
, and hence is uniformly integrable. So, X is of class (DL). Localizing, all locally integrable processes are locally of class (DL).
Any process X of class (DL) is locally of class (D), using the localizing sequence .
Now, suppose that X is cadlag, adapted, and of class (D). Setting gives
| (1) |
which, by integrability of , is integrable. So, X is locally integrable and, applying Lemma 6, this still holds whenever X is locally of class (D). ⬜
It is useful to know that local martingales, submartingales and supermartingales are locally integrable.
Lemma 10 Every local martingale, local submartingale and local supermartingale is locally integrable.
Proof: Let X be a local martingale, submartingale or supermartingale. By stability of the local integrability property, it is enough to show that X is locally a locally integrable process. So, we can suppose that X is a proper submartingale or supermartingale. Define the stopping times
for each positive integer n, and set . These times increase to infinity as n goes to infinity and inequality (1) holds. So, it just needs to be shown that
is integrable. However, as
are bounded stopping times, this is stated by optional sampling. ⬜
It is frequently useful to be able to take conditional expectations of a process at a stopping time. In general, for this to be well-defined requires the process to satisfy some integrability properties. The following lemma shows that local integrability of the process is sufficient.
Lemma 11 If X is locally
-integrable then, for any stopping time
, the conditional expectations
are almost surely-finite.
Proof: By local integrability, there exist stopping times increasing to infinity such that
is
-integrable for all n. As
and
are
-measurable,
As n goes to infinity, we have for large enough n whenever
. So, the conditional expectation on the left hand side is almost-surely finite when
. Exactly the same argument holds with
in place of
. ⬜
Prelocal integrability
Finally, I will mention that sometimes it is useful to localize a process by stopping just before stopping times , rather than at those times. This is called prelocalization, and can be useful to avoid sudden jumps in the process at inaccessible times. I do not make much use of prelocalization in these notes, but will now briefly look at prelocally integrability. Compare the following with Definition 4 above. Here,
is used to denote the left limits of the process
,
and we take to be 0.
Definition 12 A process X is prelocally integrable if
is locally in the class of integrable processes.
More generally, for any, X is prelocally
-integrable if
is locally in the class of
-integrable processes.
As , it should be clear that prelocal integrability is a weaker property than local integrability. In fact, all cadlag adapted processes are prelocally integrable.
Lemma 13 If X is a right-continuous adapted process such that, for each time t,
is almost surely finite, then X is prelocally
-integrable.
In particular, every cadlag adapted process is prelocally-integrable.
Proof: Define the stopping times
As for n greater than
, the sequence
increases to infinity under the hypothesis of the lemma. Also,
is bounded by n, so is
-integrable, and X is prelocally
-integrable.
As is finite for any cadlag process X, cadlag adapted processes are prelocally
-integrable. ⬜
Finally, Lemma 11 extends to prelocally integrable processes, although the conclusion is only of any use if X is not a progressively measurable process (e.g., if it is not adapted).
Lemma 14 If X is prelocally
-integrable then, for any stopping time
, the conditional expectation
is almost surely-finite.
Proof: The proof is almost identical to that above for Lemma 11. By prelocal integrability, there exist stopping times increasing to infinity such that
is
-integrable for all n. As
is
-measurable,
As n goes to infinity, we have for large enough n whenever
. So, the conditional expectation on the left hand side is almost-surely finite when
. ⬜
Hi,
I was wondering why is it necessary to multiply the stopped process by the indicator function over the events of the form in definition 1, then setting the resulting process to 0 over this type of events ?
in definition 1, then setting the resulting process to 0 over this type of events ?
Best regards
If you don’t do that then processes fail to be local martingales (etc) which you would really hope are of this class. Taking something really simple, suppose that X is a constant process. That is, Xt = X0 for all times t ≥ 0, where X0 is any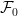 -measurable random variable. Is X a local martingale, a local submartingale, locally integrable, etc? If you don’t multiply by the indicator function {τn > 0} in the definition of localization then it will be none of these unless X0 is integrable. If you do multiply by the indicator function, then X is all of these. That’s really the reason for it. Just to make the localized classes of processes large enough that they include such simple processes.
-measurable random variable. Is X a local martingale, a local submartingale, locally integrable, etc? If you don’t multiply by the indicator function {τn > 0} in the definition of localization then it will be none of these unless X0 is integrable. If you do multiply by the indicator function, then X is all of these. That’s really the reason for it. Just to make the localized classes of processes large enough that they include such simple processes.
Got it thank’s
Very clear explanations as usual
Best Regards
Hi, I don’t yet understand your explanation of why multiplying the indicator function, can you just explain it more specifically? I would appreciate your help, thanks.
if we don’t multiply the indicator function, it would be the stopped process itself, I can’t find the difference between the stopped process and the one with indicator function
The stopped process is constant but not necessarily zero, whereas the one with the indicator function is zero whenever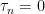 . For example, look at a constant
. For example, look at a constant 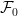 -measurable process
-measurable process  . Setting
. Setting 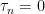 when
when  and
and 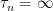 otherwise, the process
otherwise, the process  is bounded by n and is trivially a martingale, so X is a local martingale. On the other hand,
is bounded by n and is trivially a martingale, so X is a local martingale. On the other hand,  need not be integrable, and X would not be a local martingale if it is not integrable.
need not be integrable, and X would not be a local martingale if it is not integrable.
First, thank you very much for your reply. and I am so sorry for my poor basic knowledge, here is my new question: in your example, a constant \mathcal{F}_0-measurable process X_t=X_0. Setting \tau_n=0 when \lvert X_0\rvert\le n and \tau_n=\infty otherwise. So when \lvert X_0\rvert\le n , X^{\tau_n}=X_0 and its absolute value is less than n, otherwise X^{\tau_n}=X_t=X_0 and its absolute value is bigger than n. so the process 1_{\{\tau_n > 0\}}X^{\tau_n} is either zero or X_t which equals to X_0 and is bigger than n. because the process X_t=X_0 is constant, so whatever X_0 is, the expectation of X_t conditioning X_0 is X_0, which is the definition of the martingale, so either the process 1_{\{\tau_n > 0\}}X^{\tau_n} or the process X^{\tau_n}=X satisfies the martingale definition, and we can get that the process X_t is local martingale. this is my understand and I don not know where is the mistake, I hope your reply, thank you very much
The mistake is that you seem to be missing the integrability condition in the definition of a martingale. is not a martingale because
is not a martingale because ![{\mathbb E}[\lvert M_t\rvert]](https://s0.wp.com/latex.php?latex=%7B%5Cmathbb+E%7D%5B%5Clvert+M_t%5Crvert%5D&bg=ffffff&fg=000000&s=0&c=20201002) is infinite.
is infinite.
oh, I seem to understand it more, but not totally. And the example of constant process you set before is great, but maybe it should be the condition where τn is infinite when |X0| =0}Xτn is bounded by n and integrable so it’s a martingale. And you set τn is 0 when |X0| =0}Xτn maybe not integrable. Am I right?
Best regards
oh, I seem to understand it more, but not totally. And the example of constant process you set before is great, but maybe it should be the condition where τn is infinite when |X0|0}Xτn is bounded by n and integrable so it’s a martingale. And you set τn is 0 when |X0| 0}Xτn maybe not integrable. Am I right? thanks
sorry, there’s something wrong with the post, I can not type some signs regularly, so may I have your email? I would appreciate it if I could ask you some questions via email
You have mail
Update: I added a proof that local martingales, submartingales and supermartingales are locally integrable. This is a fairly basic property, and very useful, but wasn’t previously stated in these notes.
Dear George,
I was wondering why \tau_n = inf{t: |X_t| => n } goes to infinity as n goes to infinity (which seems to be implied when saying that it is a localizing sequence) for cadlag X.
Say take f(x) = 1/(1-x) * I_{x \infty holds.
But I wasn’t sure how to handle that issue in the proof of locally (D) being locally integrable in lemma 9.
Thanks again. These notes make martingale theory much more manageable to learn.
Tigran
The sequence must tend to infinity, otherwise there would be a time T for which
must tend to infinity, otherwise there would be a time T for which  holds infinitely often. This would imply that X is unbounded on the interval [0,T]. But, cadlag functions on compact intervals are always bounded.
holds infinitely often. This would imply that X is unbounded on the interval [0,T]. But, cadlag functions on compact intervals are always bounded.
Thanks for the reply. I realise that I didn’t fully write down the example I had in mind.
Take a function which continuously goes to infinity asymptotically from the left (e.g. g(x) = 1/(1-x) ). Now construct a function f(x) to be equal to g(x) that from on x in [0,1) and to be zero for x => 1. Then the function is cadlag (unless cadlag excludes limits going to infinity), but not bounded on compacts.
That example is not cadlag, because it doesn’t have a left limit at x=1. And, yes, cadlag excludes limits going to infinity.
Dear George,
I have a question related to local martingales which I thought that you might be able to answer. Your help would be very much appreciated. The question is the following:
Assume that S is a continuous loc-mtg with respect to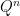 (whose radon-nikodym derivatives with respect to P are denoted by
(whose radon-nikodym derivatives with respect to P are denoted by  ),
),  . Assume that
. Assume that  P-a.s. and let Q be the measure corresponding to Z. Then, my question is if S is a local martingale wrt Q as well?
P-a.s. and let Q be the measure corresponding to Z. Then, my question is if S is a local martingale wrt Q as well?
If is a bounded mtg with respect to P for all n, then, I see that the result follows by use of e.g. dominated convergence and bayes rule. Hence, if I can find a localizing sequence
is a bounded mtg with respect to P for all n, then, I see that the result follows by use of e.g. dominated convergence and bayes rule. Hence, if I can find a localizing sequence 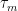 such that
such that  is a martingale for all n, then I’m done.
is a martingale for all n, then I’m done.
By assumption I know that there exists localizing sequences such that
such that  is a P-martingale. However, how do I know that there exists a localizing sequence
is a P-martingale. However, how do I know that there exists a localizing sequence 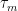 which holds for all n ?! If not, is there some other way to proceed?
which holds for all n ?! If not, is there some other way to proceed?
Would be very very happy for your help,
Best,
Hi.
Yes, S is a local martingale wrt Q. You can take the localizing sequence . Then,
. Then, 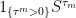 is a local Qn martingale for each n and is uniformly bounded (by m). So, it a Qn martingale and is a Q-martingale by what you said above.
is a local Qn martingale for each n and is uniformly bounded (by m). So, it a Qn martingale and is a Q-martingale by what you said above.
This just works because S is continuous. If it wasn’t, then the question is rather trickier.
(Technical note: really, the relevant mode of convergence is that in L1 but, assuming that Z has expectation 1, this is implied by almost sure convergence anyway).
in L1 but, assuming that Z has expectation 1, this is implied by almost sure convergence anyway).
Hi!
Thanks!! I have to agree with all the people saying this is one of the best blogs ever 🙂
However, now I really started wondering: If S is not continuous but a locally bounded local martingale, would it then be possible to find a sequence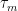 , which would work for all n as above?
, which would work for all n as above?
Very nice exposition, thank you! I think there’s a typo in the definition of the localizing sequence of stopping times under definition 3: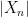 should exceed an increasing constant, say
should exceed an increasing constant, say  , instead of the fixed
, instead of the fixed  , otherwise
, otherwise  would not necessarily become infinite.
would not necessarily become infinite.
Well spotted! Thanks, I have fixed it now.
Dear George, thank you for your website! I am studying Stochastic Integration and I have a question to Definition 3. How to understand the class of uniformly bdd processes? And most importantly I do not understand an example:
you say that all continuous adapted processes are locally bounded, with the localizing sequence you mentioned. I do not see how this sequence makes something bdd. I see that saying that absolute value is $\geq n$ makes only situation worse. I.e. all r.v.-s because of this of a process $X^\{tau_n} = { X^{t_1}_1,\ldots,X^{t_\infty}_{\infty}}$ are saying that each r.v. of this sequence are bdd from below!
Could you please shed some light on my basic, probably not smart, question?
Dear George,
thanks a lot for this amazing work! I do have a question through regarding your statement that left-continuous adapted processes which are almost surely bounded on every finite time interval are automatically locally bounded. I have no problem with that statement whenever the underlying filtration is right-continuous, as I can use first-hitting times of say [n,\infty) to localise, but those would typically fail to be stopping times when the filtration is not right-continuous.
I tried to think of a counter-example: take a process which is 0 until time 1 (included) and then equal to some unbounded random variable Y after (strictly) time 1. Take F to be the natural filtration of that process, which is not right-continuous unless I am mistaken. The process is càglàd, and I expect that one can describe more or less explicitly any F-stopping time as being either deterministic or some measurable function f(Y), with f valued in (1,\infty), and I haven’t been able to create any localising sequence from this. But I could of course be missing something!
I am mainly asking as you’re using in a later post the fact that left-limits of F-adapted càdlàg processes are always locally bounded and thus in L^1(X) for any F-semimartingale X, and it could be that this statement either requires right-continuous filtrations, or maybe a different argument.
Would be happy to hear your thoughts on that!
You are right, and that is a mistake. It should hold if the filtration is right-continuous though, so the statement about being in L^1(X) will still hold true (passing to the right-continuous filtration will not change which processes are in L^1(X)).
I fixed the wording. Thanks!
Thanks a lot for getting back to me on this! I also agree that L^1(X) doesn’t change whether we consider it for F or F^+ (as long as X is adapted to F of course).
I kept going through your notes, and there are other spots where I think this may change slightly some of your statements. More precisely, in your post on « Quadratic Variations and the Itō isometry », in Lemmas 3 and 4, I have only been able to show in general that X^2 – [X] and XY – [X,Y] are F^+-martingales (since the stochastic integrals of the left-limit processes are then naturally F^+-martingales). Do you have any idea if this can be fixed?
Maybe a bit more important, you also use this in the post on « Preservation of the martingale property » during the proof of Theorem 5. When proving that 3 implies 1, you use that Y_{t-} is left-continuous to deduce that it is locally integrable, but this is again not correct in general (one can use the same counter-example as for contradicting the local-boundedness, just take a non-integrable jump size). Any thoughts on that would also be greatly appreciated!
In any case, thanks again for the beautiful work!
In all the cases mentioned, the integrands are left-limits of cadlag adapted processes, which is sufficient to show that they are locally bounded. I don’t think there is a problem. I will have to go over the wording when I have a few moments though.
Thanks for your help!
In addition, the F^+ martingales are clearly F-adapted, which is sufficient to show that they are F-martingales. However, I don’t think that it is necessary to pass to the right-continuous filtration even as an intermediate step.
I have a small doubt. In lemma 8 how did you make use of lemma 6 to prove the the converse direction i.e is locally integrable implies that
is locally integrable implies that  is locally integrable
is locally integrable
I meant the jumps of X