Properties of the Stochastic Integral

In the previous two posts I gave a definition of stochastic integration. This was achieved via an explicit expression for elementary integrands, and extended to all bounded predictable integrands by bounded convergence in probability. The extension to unbounded integrands was done using dominated convergence in probability. Similarly, semimartingales were defined as those cadlag adapted processes for which such an integral exists.

The current post will show how the basic properties of stochastic integration follow from this definition. First, if ${V}$ is a cadlag process whose sample paths are almost surely of finite variation over an interval ${[0,t]}$ , then ${\int_0^t\xi\,dV}$ can be interpreted as a Lebesgue-Stieltjes integral on the sample paths. If the process is also adapted, then it will be a semimartingale and the stochastic integral can be used. Fortunately, these two definitions of integration do agree with each other. The term FV process is used to refer to such cadlag adapted processes which are almost surely of finite variation over all bounded time intervals. The notation ${\int_0^t\vert\xi\vert\,\vert dV\vert}$ represents the Lebesgue-Stieltjes integral of ${\vert\xi\vert}$ with respect to the variation of ${V}$ . Then, the condition for ${\xi}$ to be ${V}$ -integrable in the Lebesgue-Stieltjes sense is precisely that this integral is finite.

Lemma 1 Every FV process ${V}$ is a semimartingale. Furthermore, let ${\xi}$ be a predictable process satisfying

$\displaystyle \int_0^t\vert\xi\vert\,\vert dV\vert<\infty$ (1)

almost surely, for each ${t\ge 0}$ . Then, ${\xi\in L^1(V)}$ and the stochastic integral ${\int\xi\,dV}$ agrees with the Lebesgue-Stieltjes integral, with probability one.

Proof: First, for bounded predictable integrands, the stochastic integral can simply be defined as the Lebesgue-Stieltjes integral on the sample paths. This clearly agrees with the explicit expression for elementary integrands and, by the bounded convergence theorem, satisfies bounded convergence in probability, as required.

Now, suppose that the predictable process ${\xi}$ satisfies (1), so it is integrable with respect to ${V}$ in the Lebesgue-Stieltjes sense. If ${\vert\xi^n\vert\le\vert\xi\vert}$ is a sequence of bounded predictable processes tending to a limit ${\alpha}$ then, by the dominated convergence theorem for Lebesgue integration, the following limit holds

$\displaystyle \int_0^t\xi^n\,dV\rightarrow\int_0^t\alpha\,dV$

with probability one and, therefore, also under convergence in probability. Choosing ${\alpha=0}$ shows that ${\xi\in L^1(V)}$ . Then, choosing ${\alpha=\xi}$ shows that the Lebesgue-Stieltjes integral ${\int_0^t\xi\,dX}$ agrees with the stochastic integral. ⬜

Next, associativity of integration can be shown. This is easiest to understand in the differential form, in which case, equation (2) below simply says that ${\beta(\alpha\,dX)=(\beta\alpha)\,dX}$ .

Theorem 2 (Associativity) Suppose that ${Y=\int\alpha\,dX}$ for a semimartingale ${X}$ and ${X}$ -integrable process ${\alpha}$ . Then, ${Y}$ is a semimartingale and a predictable process ${\beta}$ is ${Y}$ -integrable if and only if ${\beta\alpha}$ is ${X}$ -integrable, in which case

$\displaystyle \int\beta\,dY = \int\beta\alpha\,dX.$ (2)

Proof: That ${Y}$ is a semimartingale, and equation (2) is satisfied for bounded ${\beta}$ has already been shown in the previous post, in the proof of existence of cadlag versions of integrals. Now, suppose that ${\beta\alpha\in L^1(X)}$ , and choose a sequence of bounded predictable processes ${\vert\xi^n\vert\le\vert\beta\vert}$ tending to a limit ${\xi}$ . As ${\xi^n\alpha}$ is dominated by the ${X}$ -integrable process ${\beta\alpha}$ ,

$\displaystyle \int_0^t\xi^n\,dY=\int_0^t\xi^n\alpha\,dX\rightarrow \int_0^t\xi\alpha\,dX$

in probability, as ${n\rightarrow\infty}$ . Taking ${\xi=0}$ gives zero for the right hand side so, by definition, ${\beta\in L^1(X)}$ . Then, taking ${\xi=\beta}$ , dominated convergence in probability shows that the left hand side tends to ${\int_0^t\beta\,dY}$ , and equation (2) follows.

Conversely, suppose that ${\beta\in L^1(Y)}$ and let ${\xi^n\rightarrow 0}$ be a sequence of bounded predictable processes satisfying ${\vert\xi^n\vert\le\vert\beta\alpha\vert}$ . Writing ${\xi^n=(\xi^n1_{\{\alpha\not=0\}}\alpha^{-1})\alpha}$ , the above argument shows that ${\xi^n1_{\{\alpha\not=0\}}\alpha^{-1}\in L^1(Y)}$ and

$\displaystyle \int_0^t\xi^n\,dX=\int_0^t \xi^n 1_{\{\alpha\not=0\}}\alpha^{-1}\,dY.$

By dominated convergence, this tends to zero in probability as ${n\rightarrow\infty}$ . So, ${\beta\alpha\in L^1(X)}$ as required. ⬜

Note that, as Theorem 2 gives an `if and only if’ condition for ${\beta}$ to be ${Y}$ -integrable, the definition of ${Y}$ -integrable processes as good dominators given in these notes is precisely the correct set of processes to make this theorem hold. In fact, noting that ${(1+\vert\alpha\vert)^{-1}}$ and ${(1+\vert\alpha\vert)^{-1}\alpha}$ are bounded for any process ${\alpha}$ , associativity gives the following alternative criterion for ${X}$ -integrability and definition of stochastic integration for unbounded integrands.

Corollary 3 Let ${X}$ be a semimartingale and ${\alpha}$ be a predictable process. Then, ${\alpha}$ is ${X}$ -integrable if and only if there exists a semimartingale ${Y}$ satisfying ${Y_0=0}$ and

$\displaystyle \int(1+\vert\alpha\vert)^{-1}\,dY = \int(1+\vert\alpha\vert)^{-1}\alpha\,dX,$ (3)

in which case ${Y=\int\alpha\,dX}$ .

Proof: First, if ${\alpha\in L^1(X)}$ and ${Y=\int\alpha\,dX}$ then equation (3) follows from associativity of the stochastic integral. Conversely, suppose that ${Y}$ is a semimartingale satisfying (3) and that ${Y_0=0}$ . Letting ${Z}$ equal the integral on the left hand side of (3), associativity of integration shows that ${1+\vert\alpha\vert}$ is ${Z}$ -integrable and

$\displaystyle \int (1+\vert\alpha\vert)\,dZ=\int 1\,dY = Y.$

Similarly, as ${Z}$ is also equal to the right hand side of (3), associativity shows that ${\alpha}$ is ${X}$ -integrable and

$\displaystyle \int (1+\vert\alpha\vert)\,dZ=\int \alpha\,dX.$

Comparing these equalities gives ${Y=\int\alpha\,dX}$ as required. ⬜

Stochastic integrals behave particularly well under stopping. Recall that ${X^\tau_t\equiv X_{t\wedge\tau}}$ represents a process ${X}$ stopped at the time ${\tau}$ .

Lemma 4 Let ${X}$ be a semimartingale, ${\xi}$ be ${X}$ -integrable and ${\tau}$ be a stopping time. Then, the stopped process ${X^\tau}$ is also a semimartingale, ${\xi}$ is ${X^\tau}$ -integrable and

$\displaystyle \left(\int\xi\,dX\right)^\tau = \int 1_{(0,\tau]}\xi\,dX = \int\xi\,dX^\tau.$ (4)

Proof: Approximating ${\tau}$ by the discrete stopping times ${\tau_n=\inf\{k/n\colon k/n\ge\tau\}}$ gives

$\displaystyle \setlength\arraycolsep{2pt} \begin{array}{rl} \displaystyle\int_0^t 1_{(0,\tau_n]}\,dX &\displaystyle= \sum_{k=0}^\infty\int_0^t 1_{\{\tau > k/n\}}1_{(k/n,(k+1)/n]}\,dX\smallskip\\ &\displaystyle=\sum_{k=0}^\infty 1_{\{\tau > k/n\}}(X_{t\wedge(k+1)/n}-X_{t\wedge k/n})=X^{\tau_n}_t-X_0. \end{array}$

As ${\tau_n\downarrow \tau}$ , bounded convergence in probability can be applied,

$\displaystyle \int 1_{(0,\tau]}\,dX=\lim_{n\rightarrow\infty}\int 1_{(0,\tau_n]}\,dX=\lim_{n\rightarrow\infty}X^{\tau_n}-X_0=X^\tau-X_0.$

Associativity of the stochastic integral shows that ${X^\tau}$ is a semimartingale, ${\xi\in L^1(X^\tau)}$ and, by integrating ${\xi}$ , gives the right hand equality of (4).

Similarly, integrating ${1_{(0,\tau]}}$ with respect to ${Y\equiv\int\xi\,dX}$ gives,

$\displaystyle Y^\tau=\int 1_{(0,\tau]}\,dY=\int 1_{(0,\tau]}\xi\,dX$

as required. ⬜

Next, the class of ${X}$ -integrable processes is unchanged under localization.

Lemma 5 Let ${X}$ be a semimartingale. Then, a predictable process ${\xi}$ is ${X}$ -integrable if and only if it is locally ${X}$ -integrable.

Proof: If ${\xi}$ is locally ${X}$ -integrable then there exist stopping times ${\tau_n\uparrow\infty}$ such that ${1_{(0,\tau_n]}\xi\in L^1(X)}$ . Choose bounded predictable processes ${\vert\xi^k\vert\le\vert\xi\vert}$ which tend to zero as ${k}$ goes to infinity. Then, for any fixed ${n}$ , ${1_{(0,\tau_n]}\xi^k}$ are dominated by ${1_{(0,\tau_n]}\xi}$ . So, equation (4) and dominated convergence in probability give

$\displaystyle 1_{\{\tau_n\ge t\}}\int_0^t\xi^k\,dX =1_{\{\tau_n\ge t\}}\int_0^{t\wedge\tau_n}\xi^k\,dX =1_{\{\tau_n\ge t\}}\int_0^t1_{(0,\tau_n]}\xi^k\,dX \rightarrow 0$

in probability as ${k\rightarrow\infty}$ . By choosing ${n}$ large, ${{\mathbb P}(\tau_n\ge t)}$ can be made as close to 1 as required, showing that ${\int_0^t\xi^k\,dX}$ goes to zero in probability. So, by definition, ${\xi\in L^1(X)}$ . ⬜

A consequence of this result is the following important statement, which applies to all semimartingales; all locally bounded predictable processes are ${X}$ -integrable. In particular, if ${Y}$ is a cadlag adapted process then its left limits ${Y_{t-}}$ give a left-continuous and adapted, hence predictable, process. It is, furthermore, locally bounded and the integral ${\int Y_{t-}\,dX_t}$ is well defined.

A similar result as above shows that the class of semimartingales is closed under localization.

Lemma 6 A stochastic process is a semimartingale if and only if it is locally a semimartingale.

Proof: By definition, a process ${X}$ is locally a semimartingale if there are stopping times ${\tau_n\uparrow\infty}$ such that ${1_{\{\tau_n>0\}}X^{\tau_n}}$ are semimartingales. Then, ${X^{\tau_n}=1_{\{\tau_n>0\}}X^{\tau_n}+1_{\{\tau_n=0\}}X_0}$ are semimartingales. For any bounded predictable process ${\xi}$ and ${m\ge n}$ , Lemma 4 gives

$\displaystyle \int_0^{t\wedge \tau_n}\xi\,dX^{\tau_m} =\int_0^t\xi\,dX^{\tau_m\wedge\tau_n}=\int_0^t\xi\,dX^{\tau_n}.$

In particular ${\int_0^t\xi\,dX^{\tau_m}=\int_0^t\xi\,dX^{\tau_n}}$ whenever ${\tau_n\ge t}$ . So, we can define the integral with respect to ${X}$ by

$\displaystyle \int_0^t\xi\,dX=\lim_{n\rightarrow\infty}\int_0^t\xi\,dX^{\tau_n}$

where the limit on the right hand side is eventually constant, with probability one. This clearly satisfies the explicit expression for elementary integrands. To show that ${X}$ is a semimartingale, it only remains to prove bounded convergence in probability. So, suppose that ${\xi^k\rightarrow\xi}$ is a uniformly bounded sequence of predictable processes. Dominated convergence in probability can be applied to the semimartingale ${X^{\tau_n}}$ ,

$\displaystyle \setlength\arraycolsep{2pt} \begin{array}{rl} &\displaystyle 1_{\{\tau_n\ge t\}}\int_0^t\xi^k\,dX = 1_{\{\tau_n\ge t\}}\int_0^t\xi^k\,dX^{\tau_n}\smallskip\\ &\quad\quad\displaystyle \rightarrow 1_{\{\tau_n\ge t\}}\int_0^t\xi\,dX^{\tau_n}= 1_{\{\tau_n\ge t\}}\int_0^t\xi\,dX. \end{array}$

Then, by choosing ${n}$ large enough, ${{\mathbb P}(\tau_n\ge t)}$ can be made as close to 1 as required, showing that ${\int_0^t\xi^k\,dX}$ does indeed converge in probability ${\int_0^t\xi\,dX}$ . ⬜

Let us now move on to the dominated convergence theorem. Although dominated convergence in probability was required by the definition of stochastic integration, convergence also holds in a much stronger sense. A sequence of processes ${Y^n}$ converges ucp to a limit ${Y}$ if ${\sup_{s\le t}\vert Y^n_s-Y_s\vert}$ tends to zero in probability for each ${t\ge 0}$ .

Theorem 7 (Dominated Convergence) Let ${X}$ be a semimartingale and ${\xi^n}$ be a sequence of predictable processes converging to a limit ${\xi}$ . If the sequence is dominated by some ${X}$ -integrable process ${\alpha}$ , so that ${\vert\xi^n\vert\le\vert\alpha\vert}$ , then

$\displaystyle \int\xi^n\,dX\xrightarrow{\rm ucp}\int\xi\,dX$

and, furthermore, convergence holds in the semimartingale topology.

Proof: As semimartingale convergence implies ucp convergence, it is enough to show that ${Y^n\equiv\int\xi^n\,dX-\int\xi\,dX}$ converges to zero in the semimartingale topology. Choose a sequence ${\vert\zeta^n\vert\le 1}$ of elementary predictable processes. Then, ${\vert\zeta^n(\xi^n-\xi)\vert\le 2\vert\alpha\vert}$ , and dominated convergence in probability gives

$\displaystyle \int_0^t\zeta^n\,dY^n=\int_0^t\zeta^n(\xi^n-\xi)\,dX\rightarrow 0$

in probability as ${n\rightarrow\infty}$ . By definition, this proves semimartingale convergence. ⬜

The dominated convergence theorem can be used to prove the following result stating that the jumps of a stochastic integral behave in the expected way. Recall that the jump ${\Delta X_t}$ of a cadlag process is equal to ${X_t-X_{t-}}$ . In these notes, when two processes are shown to be equal, this is always taken to mean that they agree up to evanescence.

Corollary 8 If ${X}$ is a semimartingale and ${\xi\in L^1(X)}$ then

$\displaystyle Y=\int\xi\,dX\ \Rightarrow\ \Delta Y=\xi\,\Delta X.$ (5)

Proof: Let ${V}$ be the set of all ${X}$ -integrable processes such that equation (5) is satisfied. This contains all elementary predictable processes, by the explicit expression for the integral. Consider a sequence ${\xi^n\in V}$ which is dominated by some ${\alpha\in L^1(X)}$ and suppose that ${\xi^n\rightarrow \xi}$ . If it can be shown that ${\xi\in V}$ then the functional monotone class theorem will imply that ${V=L^1(X)}$ , as required.

By Theorem 7, ${Y^n\equiv\int\xi^n\,dX}$ converges ucp to ${Y\equiv\int\xi\,dX}$ . Passing to a subsequence if necessary, we may suppose that, almost surely, the sample paths converge uniformly on compacts. Then, the following limits hold uniformly on compacts,

$\displaystyle \Delta Y=\lim_{n\rightarrow\infty}\Delta Y^n=\lim_{n\rightarrow\infty}\xi^n\,\Delta X=\xi\,\Delta X.$

⬜

Stochastic integration preserves certain properties of processes, such as continuity and predictability.

Corollary 9 Suppose that ${Y=\int\xi\,dX}$ for a semimartingale ${X}$ and ${\xi\in L^1(X)}$ . If ${X}$ is continuous (resp. predictable) then so is ${Y}$ .

Proof: If ${X}$ is continuous then equation (5) shows that ${\Delta Y=\xi\Delta X=0}$ , so ${Y}$ is continuous.

For any cadlag process ${X}$ , its left-limit ${X_{-}}$ is a left-continuous and adapted process which, by definition, is predictable. So, ${X}$ is predictable if and only if ${\Delta X=X-X_{-}}$ is. So, suppose that ${X}$ is predictable. Then, (5) shows that ${Y}$ is also predictable. ⬜

Finally, the set of semimartingales is a vector space, and stochastic integration ${\int\xi\,dX}$ is linear in the integrator ${X}$ .

Lemma 10 Let ${X,Y}$ be semimartingales and ${\lambda,\mu}$ be real numbers. Then, ${Z=\lambda X+\mu Y}$ is a semimartingale. Furthermore, any process ${\xi}$ which is both ${X}$ -integrable and ${Y}$ -integrable is also ${Z}$ -integrable and,

$\displaystyle \int\xi\,dZ = \lambda\int\xi\,dX + \mu\int\xi\,dY.$ (6)

Proof: The integral of any bounded predictable process ${\xi}$ with respect to ${Z}$ can be defined by (6). This clearly satisfies the explicit expression for elementary integrands, and satisfies bounded convergence in probability, as required. So, ${Z}$ is a semimartingale. Now, suppose that ${\xi\in L^1(X)\cap L^1(Y)}$ . If ${\vert\xi^n\vert\le\vert\xi\vert}$ is a sequence of bounded predictable processes tending to a limit ${\alpha}$ , then dominated convergence in probability with respect to ${Y}$ and ${Z}$ gives

$\displaystyle \int_0^t\xi^n\,dZ=\lambda\int_0^t\xi^n\,dX+\mu\int_0^t\xi^n\,dY\rightarrow \lambda\int_0^t\alpha\,dX+\mu\int_0^t\alpha\,dY$

in probability as ${n\rightarrow\infty}$ . Taking ${\alpha=0}$ , the right hand side is zero and, by definition, ${\xi\in L^1(Z)}$ . Then, taking ${\alpha=\xi}$ , dominated convergence shows that the left hand side tends to ${\int_0^t\xi\,dX}$ , giving (6). ⬜

16 thoughts on “Properties of the Stochastic Integral”

Zhenyu (Rocky) Cui says:

21 February 12 at 4:55 PM

Dear George,

Talking about the Corollary 9 here, I am wondering whether the stochastic integration preserves the α-order Holder continuity of the integrator process X. For example, consider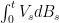 $\int_0^t V_s dB_s$ , with V an adapted process and B a standard Brownian motion. It is well-known that almost surely, B is Holder continuous with order α ∈ (0,1/2).

Now my question is: is this Ito integral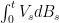 $\int_0^t V_s dB_s$ also Holder continuous with the same order α? If not, what additional conditions do we need to make it so? I personally think that this should depend on the properties of the process V, but can not find reference on this. A positive answer or a counter-example are both welcome!

Thanks in Advance!

Rocky

1. George Lowther says:
  
  22 February 12 at 2:17 AM
  
  Hi. No, the integral does not have to be Holder continuous. It’s getting late here, so I don’t have time to construct a detailed example.
  Just restricting to deterministic V, you can ensure that the integral fails to satisfy any given modulus of continuity. To do this, consider the integral as a time change of Brownian motion and use the law of the iterated logarithm. By a similar time-change argument, you just need to look at the modulus of continuity of $\int_0^t V^2_s ds$ to find sufficient conditions for the stochastic integral to be Holder continuous.
  
Tigran says:

10 April 12 at 3:08 PM

Hi George,

I am curious how you define Lebesgue Stieltjes in Lemma 1 for non-Riemann integrable integrands (can even be the classical deterministic example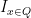 $I_{x \in Q}$ ). Is there a Legesque integral equivalent for the pathwise integral? Sorry if this is a very primitive question 🙂 Thanks in advance.

P.S.: There seems to be a small typo in the second paragraph of the proof of theorem 2: It should say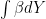 $\int \beta dY$ (not dX).

[GL: I edited your LaTeX]

1. George Lowther says:
  
  12 April 12 at 1:20 AM
  
  Given any right-continuous finite variation function $f\colon[0,t]\to\mathbb{R}$ you can define the Lebesgue-Stieltjes integral
  
  $\displaystyle\int_0^t g(s)\,df(s)$
  
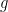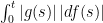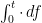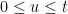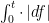  for bounded measurable $g$ , and more generally whenever $\int_0^t\vert g(s)\vert\,\vert df(s)\vert$ is measurable. Here, $\int_0^t \cdot\,df$ is a finite signed measure on (0,t] satisfying $\int_0^t1_{(0,u]}\,df=f(u)-f(0)$ for $0\le u\le t$ , and $\int_0^t\cdot\,\vert df\vert$ is its variation. This is quite standard, and I’ll give you a reference when I get a moment to look it up. It’s probably easiest to show that this is well-defined for f an increasing function (and generalize by looking at the difference of increasing functions). In that case, you can write the integral as
  
  $\displaystyle\int_0^tg(s)\,df(s)=\int_{f(0)}^{f(1)} g(f^{-1}(y))\,dy$
  
  where I have set $f^{-1}(y)=\inf\{s\in(0,t]\colon f(s)\ge y\}$ .
  
Dominic says:

9 January 13 at 2:45 AM

Hi, I was wondering, if two integrable previsable processes are indistinguishable, can we say that their integrals are equal almost surely? Don’t seem to remember that being mentioned..

1. Dominic says:
  
  9 January 13 at 10:00 AM
  
  Hmm, I see for indistinguishable, surely left continuous integrands this follows by step function approximation (as the statement is certainly true for simple integrands). Perhaps the full general case follows by an MCT argument…
  
  1. Dominic says:
    
    18 January 13 at 8:22 AM
    
    ..now having read onwards, I see that we can use the Itou isometry even for discontinuous local martingales, giving the result.
    
Johannes says:

28 February 15 at 12:55 PM

The definition of “local integrability” in Lemma 5 seems different from the one given on the “Localization”-Page where the running supremum has to be locally integrable. Does the latter refer to the finiteness of the expectations at all times and has nothing to do with stochastic integration?

1. George Lowther says:
  
  6 June 16 at 3:41 AM
  
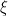  “locally X-integrable” has a different meaning to “locally integrable”. The first means that there exist stopping times $\tau_n$ increasing to infinity such that $1_{(0,\tau_n]}\xi$ are X-integrable. i.e., $\xi$ is X-integrable in a local sense. In the second, integrability refers to finite expectation, and the running supremum is also used (as this behaves better under localisation then just looking at the integrability at fixed times).
  
Paula Rowińska says:

30 April 17 at 5:16 PM

Hello, thank you for the post. Could you provide any sources?

1. George Lowther says:
  
  20 May 17 at 1:20 PM
  
  The results here are all fairly standard. I’ll post some of my references when I have a moment, and I think I’ll create a page on this blog to list my stochastic calculus references.
  
Richard Guo says:

26 May 20 at 8:47 AM

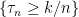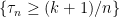Minor correction: in the first display after Eq. (4), $\{\tau_n \geq k / n\}$ should perhaps be replaced by $\{\tau_n \geq (k+1)/n \}$ .

1. George Lowther says:
  
  27 May 20 at 10:46 AM
  
  Hi Richard. You are correct – I fixed. Thanks!
  
bluig says:

13 January 21 at 2:11 PM

I have a question about the dominated convergence theorem as stated here (and elsewhere).
It is unclear to me whether the limit $\xi$ is assumed to be predictable or not. If it is not predictable (and if the predictability does not follow from the assumptions) then one must extend the concept of the integral for such processes.

1. George Lowther says:
  
  13 January 21 at 3:21 PM
  
  A pointwise limit of (real-valued) measurable functions is itself measurable, so yes the limit must be predictable.
  
  1. bluig says:
    
    13 January 21 at 4:13 PM
    
    I was suspecting this was the answer but because we are dealing with an underlying product space \Omega\times\mathbb{\R} I did not quite see it, but I do now. Thank you!

	Harry on Filtrations and Adapted P…
	Anonymous on Analytic Sets
	Daniel on Analytic Sets
	Sid on Martingale Convergence
	northwiz on Preservation of the Local Mart…
	George Lowther on Martingale Convergence
	Sid on Martingale Convergence
	George Lowther on The Burkholder-Davis-Gundy Ine…
	George Lowther on Preservation of the Local Mart…
	northwiz on Preservation of the Local Mart…

Properties of the Stochastic Integral

Published by George Lowther

16 thoughts on “Properties of the Stochastic Integral”

Leave a Reply to Dominic Cancel reply

Like this:

Related

Published by George Lowther

16 thoughts on “Properties of the Stochastic Integral”

Leave a Reply to Dominic Cancel reply