Recall that Ito’s lemma expresses a twice differentiable function applied to a continuous semimartingale
in terms of stochastic integrals, according to the following formula
| (1) |
In this form, the result only applies to continuous processes but, as I will show in this post, it is possible to generalize to arbitrary noncontinuous semimartingales. The result is also referred to as Ito’s lemma or, to distinguish it from the special case for continuous processes, it is known as the generalized Ito formula or generalized Ito’s lemma.
If equation (1) is to be extended to noncontinuous processes then, there are two immediate points to be considered. The first is that if the process is not continuous then it need not be a predictable process, so
need not be predictable either. So, the integrands in (1) will not be
-integrable. To remedy this, we should instead use the left limits
in the integrands, which is left-continuous and adapted and therefore is predictable. The second point is that the jumps of the left hand side of (1) are equal to
and, on the right, they are
. There is no reason that these should be equal, and (1) cannot possibly hold in general. To fix this, we can simply add on the correction to the jump terms on the right hand side,
| (2) |
By using a second order Taylor expansion of , the term inside the summation is almost surely bounded by a multiple of
. As it was previously shown that the jumps of a semimartingale satisfy
, the summation above is guaranteed to be absolutely convergent. So, equation (2) makes sense, and the jump sizes on both sides agree. In fact, (2) is true for for all semimartingales, and this is precisely the generalized Ito formula for one dimensional processes.
Before giving the full statement, it helps to introduce a bit of notation to simplify things a bit. Any FV process can be split into two parts. Its purely discontinuous part is the sum of its jumps,
, and its purely continuous part is
. In particular, I will make use of the purely continuous parts of the quadratic variation and covariations of semimartingales
Note that, by canceling with the quadratic term in the summation, the quadratic variation
in equation (2) can be replaced by its continuous part. This simplifies the equations a bit.
Next, any jointly measurable process , which is only ever nonzero on a countable set of times and satisfies
, can be alternatively be considered as a differential. This is done by simply replacing integration with summation. That is,
This notation enables equation (2) to be expressed in differential notation. Also, the continuous part of the quadratic covariation can be written as
.
A d-dimensional process is said to be a semimartingale if each of its components
are semimartingales and finally, as in the previous post, I am using the summation convention where indices which occur twice in a single term are summed over. The full statement of the generalized Ito formula using differential notation is then as follows.
Theorem 1 (Generalized Ito Formula) Let
be a d-dimensional semimartingale such that
take values in an open subset
. Then, for any twice continuously differentiable function
,
is a semimartingale and,
(3)
The final two terms on the right hand side of (3) are FV processes. Sometimes, we are only concerned about describing a process up to a finite variation term, in which case the following much simplified version of Ito’s formula can be useful.
Corollary 2 Let
be a d-dimensional semimartingale and
be twice continuously differentiable. Then,
for some FV process
.
For example, FV processes only contribute pure jump terms to quadratic covariations and therefore do not contribute at all to the continuous part. So, Corollary 2 has the following consequence.
Corollary 3 Let
be a d-dimensional semimartingale and
be twice continuously differentiable. Then,
for any semimartingale
.
Example: The Doléans exponential
As previously mentioned, the Doléans exponential of a semimartingale is the solution to the integral equation
and is denoted by . This can be solved with the help of the generalized Ito formula. The continuous part of the quadratic variation satisfies
and the jumps are
. Assuming that
remains positive, the generalized Ito formula gives,
| (4) |
Here, I have applied the identity
Integrating (4) gives,
Exponentiating gives the following formula for the Doléans exponential of a general semimartingale
| (5) |
This gives the general form for the Doléans exponential, but, a brief comment on the derivation above is in order. In order to apply the logarithm, it was assumed that the process remains positive. However, from (5) it can be seen that it goes negative or zero if there is a jump . This problem is not difficult to fix by splitting the process
into two terms, one with the jumps less than -1 removed and the other only containing such jumps. Then, the argument above holds when applied to the first term, and it is easily verified that equation (5) remains true after adding in the second, piecewise constant, term.
Proof of Ito’s Formula
Writing out equation (3) in integral form, and substituting in the quadratic covariation rather than just its continuous part gives the following,
| (6) |
We now prove this formula. As the terms on the right hand side are all FV processes or stochastic integrals, this also shows that is a semimartingale.
For any times , writing
, a Taylor expansion to second order gives
| (7) |
The set is almost surely a closed and bounded subset of
, for each time
. It follows that the remainder term
is almost surely of size
uniformly over the interval
. So,
whenever
over
.
Now, for a given integer n, partition the interval into n equal segments. That is, set
for
. Using the notation
, sum (7) over the intervals
,
| (8) |
The aim is to show that this converges to equation (6) in the limit as n goes to infinity. The first two summations have already been dealt with in the previous post, where it was shown that the following limits hold in probability as .
So, the first three terms on the right hand side of equation (8) do indeed converge to the first three terms on the right hand side of (6). It only remains to show that the remainder term converges to the summation in (6). Note that the remainders
satisfy
as with
. The result is then given by the following.
Lemma 4 Let
be a d-dimensional semimartingale and
be of size
uniformly over the interval
. Suppose, furthermore, that there is a process
satisfying
(9) as
over
for all times
.
Then
is almost surely finite and,
(10) in probability as
.
Proof: The condition that is of size
means that, for
, the random variables
tend to zero in the limit . In particular,
for some random variable V and, by taking limits,
giving,
I now split the proof up into two cases. First, where is zero for small values of
, and then when it is zero for large values of
.
So, suppose that whenever
, for some positive
. Then, limit (10) holds almost surely. In fact, for large enough n, the terms
will all be zero except for those intervals
in which
has a jump of magnitude at least
. So it reduces to a finite sum, and the limit follows from applying (9) to each term.
Now, suppose that whenever
. Then,
| (11) |
in probability as .
We can now piece these cases together. For any , choose a continuous function
such that
is equal to 1 for
and equal to zero for
.
Applying limit (10) to the terms and (11) to
gives the following,
in probability as . By choosing
small, the right hand side can be made as small as we like, showing that
in probability as . ⬜
Hi, I think there’s a minus sign missing from the integrand in theorem 1.
Is there any reason to not just give the formula as![df(X) = D_if(X_-)dX^{i,c} + D_{ij}f(X_-)d[X^i,X^j]^c + \sum_{s\le t}\Delta f(X_s)](https://s0.wp.com/latex.php?latex=df%28X%29+%3D+D_if%28X_-%29dX%5E%7Bi%2Cc%7D+%2B+D_%7Bij%7Df%28X_-%29d%5BX%5Ei%2CX%5Ej%5D%5Ec+%2B+%5Csum_%7Bs%5Cle+t%7D%5CDelta+f%28X_s%29&bg=ffffff&fg=000000&s=0&c=20201002) ?
?
Oh right, the summation term needn’t converge, so we need the compensation terms from the first integral at least. I see.
Hello,
When the function f is one dimensional, it is easy to understand what is \Delta f (X_s) = f (X_s + jump ) – f( X_s). But what is the signification of \Delta f (X_s) when f is a two dimensional function for example?
Is it \Delta f (X_s, Y_s) = f(X_s + jump of X_s, Y_s + jump of Y_s) – f ( X_s, Y_s) ?
or \Delta f (X_s, Y_s) = f(X_s + jump of X_s, jump of Y_s) – f ( X_s, Y_s) + (X_s, jump of Y_s) – f ( X_s, Y_s + jump of Y_s).
Thank you !
Hi,
Thanks for this great answer. We wanted to cite this generalized Ito’s lemma in our paper and were wondering what is a good reference to cite.
Dear George,
How do we know that the function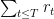 in Lemma 4 is measurable ?
in Lemma 4 is measurable ?
Use the fact that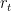 is only ever zero at times at which X jumps. So, there is a sequence of random times (actually, stopping times) Tn which includes all the times when r is nonzero. Hence, the sum can be written as
is only ever zero at times at which X jumps. So, there is a sequence of random times (actually, stopping times) Tn which includes all the times when r is nonzero. Hence, the sum can be written as  , which is a countable sum of measurable terms, so is measurable.
, which is a countable sum of measurable terms, so is measurable.
Alternatively, the result itself implies that this is a limit (in probability or almost sure, either works) of measurable random variables, so is measurable.
Dear George,
Since![U(\epsilon) \sum_{k = 1}^{n} \Vert\delta_{n,k}X\Vert^2 \le U(\epsilon) [X^i,X^i]](https://s0.wp.com/latex.php?latex=U%28%5Cepsilon%29+%5Csum_%7Bk+%3D+1%7D%5E%7Bn%7D+%5CVert%5Cdelta_%7Bn%2Ck%7DX%5CVert%5E2+%5Cle+U%28%5Cepsilon%29+%5BX%5Ei%2CX%5Ei%5D&bg=ffffff&fg=000000&s=0&c=20201002) can’t we put in the conclusion of lemma 4 the stronger statement that
can’t we put in the conclusion of lemma 4 the stronger statement that  almost sure instead of probability ?
almost sure instead of probability ?
Actually, I think you can. Convergence in probability is sufficient for our purposes, but the stronger statement should also hold.
I can’t understand why the final terms in (3) or (6) FV processes. Could you explain this to me?
The final terms are a sum over discrete jump terms. These are absolutely convergent (they must be for the sum to make sense), so give FV processes. , which has a finite sum for any semimartingale X.
, which has a finite sum for any semimartingale X.
As f is twice differentiable, these terms are all of order