
The motivation for developing a theory of stochastic integration is that many important processes — such as standard Brownian motion — have sample paths which are extraordinarily badly behaved. With probability one, the path of a Brownian motion is nowhere differentiable and has infinite variation over all nonempty time intervals. This rules out the application of the techniques of ordinary calculus. In particular, the Stieltjes integral can be applied with respect to integrators of finite variation, but fails to give a well-defined integral with respect to Brownian motion. The Ito stochastic integral was developed to overcome this difficulty, at the cost both of restricting the integrand to be an adapted process, and the loss of pathwise convergence in the dominated convergence theorem (convergence in probability holds intead).
However, as I demonstrate in this post, the stochastic integral represents a strict generalization of the pathwise Lebesgue-Stieltjes integral even for processes of finite variation. That is, if V has finite variation, then there can still be predictable integrands such that the integral
is undefined as a Lebesgue-Stieltjes integral on the sample paths, but is well-defined in the Ito sense. The relevant result from the notes is the following. Recall that an FV process is a cadlag adapted process of finite variation over all bounded time intervals.
Lemma 1 Every FV process V is a semimartingale. Furthermore, let
be a predictable process satisfying
almost surely, for each
. Then,
and the stochastic integral
agrees with the Lebesgue-Stieltjes integral, with probability one.
The condition that is finite is equivalent to
being V-integrable in the pathwise Lebesgue-Stieltjes sense. So Lemma 1 tells us that being pathwise V-integrable implies integrability in the Ito sense, and that the two definitions of the integral are in agreement. It is natural to ask about the converse: is being integrable in the stochastic sense sufficient to guarantee integrability as a pathwise Lebesgue-Stieltjes integral? The answer is, in general, no it isn’t. I give an example below of an FV process V and predictable
such that
is almost-surely infinite, so the pathwise integral does not exist, but for which
is V-integrable in the stochastic sense. The resulting integral
is then not an FV process. So, this example also demonstrates that stochastic integration does not preserve FV processes.
Before going ahead and constructing the example, it is worth noting that V must be a noncontinuous process. In fact, it can be shown that if V is a continuous FV process, then a predictable process is V-integrable if and only if it is almost-surely Lebesgue-Stieltjes integrable. This simple result will be covered later in my stochastic calculus notes but, for now, I just state it here without any proof.
Let us now construct to be a finite variation martingale. It will then have quadratic variation
and, a sufficient condition for a predictable process to be V-integrable is that
has finite expectation for each time t. Choose any infinite sequence of distinct times in the unit interval [0,1]. For example,
as in Figure 1. Also, choose a sequence of independent random variables
defined on a (complete) probability space
, each with
. The process V is then defined by the following absolutely convergent sum,
This is a cadlag pure jump process with and variation
. Let
be its natural filtration. That is,
is the sigma-algebra generated by the random variables
and the
-null sets. Then,
is a complete filtered probability space with respect to which V is an FV process. It is furthermore the case that V is a square integrable martingale. In fact, it has the independent increments property, so that
is independent of
with zero mean, for
.
Next, let be the process
This is measurable and deterministic, so is certainly predictable. It will also be V-integrable since
is bounded. By dominated convergence, its integral with respect to V is the sum over n of the integrals of , with convergence in probability.
This expresses as a sum of the independent variables
with zero mean, and with bounded sum of squares
. So, by martingale convergence for
-bounded martingales, this sum converges almost surely. The jumps of W are
This gives the variation of W as
So, W is not an FV process. Similarly,
so is not pathwise V-integrable.
In this example, only the values of at the times
mattered. In the case where
we could have instead used the piecewise continuous integrand
which still satisfies
as above.
One comment about the example given above is that, although the Lebesgue-Stieltjes integral over the unit interval is undefined on the sample paths, the improper integral does still exist. At least, this is true for the choice . Then,
is bounded on
for any time
so
is well defined on the individual sample paths, and
with almost-sure convergence. However, other choices of can be used so that
is infinite for all
, so the Lebesgue-Stieltjes integral is not well defined in the neighbourhood of any point in the unit interval.

For example, suppose that have uniform density on the unit interval,
as for all
. This happens if we let
be the fractional part of
for any irrational number
, by Weyl’s equidistribution theorem. Then,
satisfies
as
and
Integration by parts can be applied to this integral,
The final integral on the right hand side has integrand converging asymptotically to as
, so the integral diverges at rate
. This shows that
is infinite on all nonempty subintervals
, so the pathwise integral
is undefined, even as an improper integral. An example sample path with
is shown in Figure 2.
In fact, it can be shown that if V is a continuous FV process, then a predictable process is V-integrable if and only if it is almost-surely Lebesgue-Stieltjes integrable.
how this thing can be proved?
This is a result which will appear in the stochastic calculus notes I’ve been posting. It will probably be a while before I get to that point though. [Update: The relevant post in the stochastic calculus notes is Continuous Semimartingales, Theorem 2 and the following comment.] You can prove it as follows:
i) If a predictable process ξ is V-integrable in the Lebesgue-Stieltjes sense then it will be integrable in the Ito sense, and the two integrals agree (almost surely). See here for the proof in my notes. Only the converse remains.
ii) If V is increasing and ξ is V-integrable in the Ito sense, then it is integrable in the L-S sense. To prove this, choose bounded predictable processes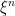 increasing to
increasing to  . Then,
. Then,  in probability (dominated convergence for stochastic integration). The left hand side agrees for the Ito and L-S integrals. If ξ wasn’t V-integrable in the L-S sense then the left hand side would tend to infinity (monotone convergence), contradicting convergence in probability.
in probability (dominated convergence for stochastic integration). The left hand side agrees for the Ito and L-S integrals. If ξ wasn’t V-integrable in the L-S sense then the left hand side would tend to infinity (monotone convergence), contradicting convergence in probability.
iii) If V is a continuous FV process then there is a predictable process |α| = 1 such that is increasing. To prove this, let Wt be the variation of V over [0,t], which is continuous and increasing. V is absolutely continuous with respect to W (i.e.,
is increasing. To prove this, let Wt be the variation of V over [0,t], which is continuous and increasing. V is absolutely continuous with respect to W (i.e.,  ). Then,
). Then,  for a predictable ξ (see here for a proof from my notes). Taking
for a predictable ξ (see here for a proof from my notes). Taking  , you can show that |α| = 1 in the dV-almost everywhere sense.
, you can show that |α| = 1 in the dV-almost everywhere sense.
iv) Choosing |α| = 1 such that is increasing then,
is increasing then,
holds in both the Ito and L-S senses, and the RHS is equivalent for Ito and L-S integrals.
Continuity is only required in the proof of step (iii), where the result that continuous FV martingales are constant is used. More generally, it is only necessary for V to be a predictable FV process, as all predictable FV martingales are constant. In fact, all predictable and cadlag martingales are continuous (which will appear in my notes later).
thanks a lot~~
Hi, in quite the same order of question that the preceding one,
If is a FV (on compacts) semimartinagle and
is a FV (on compacts) semimartinagle and 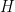 is only a càglàd (left continuous process with right limit) adapted process (a property stronger than predictability), then does the stochastic integral and the Lebesgue-Stieltjes integral always match (modulo indistinguishability) ?
is only a càglàd (left continuous process with right limit) adapted process (a property stronger than predictability), then does the stochastic integral and the Lebesgue-Stieltjes integral always match (modulo indistinguishability) ?
Short answer: Yes, they always match.
The Lebesgue-Stieltjes integral exists whenever
exists whenever  is (almost surely) finite. Assuming that H is predictable, this also means that it is X-integrable in the stochastic sense and that the two types of integral do agree (the relevant statement from my notes is here, as also linked in the post above).
is (almost surely) finite. Assuming that H is predictable, this also means that it is X-integrable in the stochastic sense and that the two types of integral do agree (the relevant statement from my notes is here, as also linked in the post above).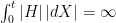 . This cannot happen if H is càglàd, because càglàd processes are almost surely bounded on compacts.
. This cannot happen if H is càglàd, because càglàd processes are almost surely bounded on compacts.
So, the only way that the two types of integration can fail to agree is if the Lebesgue-Stieltjes integral actually fails to be defined with positive probability. That is, if
Thanks for the very clear answer and argument.
By the way there is paper by M. Nutz (on ArXiv) about a version of a path-by-path construction of the Stochastic Integral with respect to Semimartingale (under some rather soft conditions over the integrator process). I thought you would be interested.
Regards.
Thanks. I haven’t had chance yet, but I’ll take a look at that paper.
I took a look at Nutz’ paper, he didn’t have integrability condition. But he has Assumption 2.1 instead. Is this assumption eough?
No, Assumption 2.1 in the paper is not to do with integrability. He is dealing with constructing the stochastic integral simultaneously with respect to a whole collection of probability measures, and the assumption implies that X satisfies the semimartingale condition in a (roughly) uniform sense under this collection of measures. For the case of a single probability measure, Assumption 2.1 is automatically satisfied whenever X is a semimartingale. Also, Assumption 2.1 does not involve the integrand H at all, so can not be about integrability of H.
The paper does have an integrability condition, although it is not stated as a numbered and boldface “Assumption”. One paragraph above Assumption 2.1, see the line “…let H be a predictable process which is X-integrable under each P ∈ 𝒫…”.
hi guys
to me, the following is an important point. what fails is pathwise stieltjess integration. on the other hand, there do exist pathwise constructions of stochastic integrals. for brownian integrals, these can be obtained using hermite polynomials. for general semimartingales, look at the works of karandikar and even more interestingly of talay and doss.
regards,
salem