Although this post is under the heading of `the general theory of semimartingales’ it is not, strictly speaking, about semimartingales at all. Instead, I will be concerned with a characterization of predictable stopping times. The reason for including this now is twofold. First, the results are too advanced to have been proven in the earlier post on predictable stopping times, and reasonably efficient self-contained proofs can only be given now that we have already built up a certain amount of stochastic calculus theory. Secondly, the results stated here are indispensable to the further study of semimartingales. In particular, standard semimartingale decompositions require some knowledge of predictable processes and predictable stopping times.
Recall that a stopping time is said to be predictable if there exists a sequence of stopping times
increasing to
and such that
whenever
. Also, the predictable sigma-algebra
is defined as the sigma-algebra generated by the left-continuous and adapted processes. Stated like this, these two concepts can appear quite different. However, as was previously shown, stochastic intervals of the form
for predictable times
are all in
and, in fact, generate the predictable sigma-algebra.
The main result (Theorem 1) of this post is to show that a converse statement holds, so that is in
if and only if the stopping time
is predictable. This rather simple sounding result does have many far-reaching consequences. We can use it show that all cadlag predictable processes are locally bounded, local martingales are predictable if and only if they are continuous, and also give a characterization of cadlag predictable processes in terms of their jumps. Some very strong statements about stopping times also follow without much difficulty for certain special stochastic processes. For example, if the underlying filtration is generated by a Brownian motion then every stopping time is predictable. Actually, this is true whenever the filtration is generated by a continuous Feller process. It is also possible to give a surprisingly simple characterization of stopping times for filtrations generated by arbitrary non-continuous Feller processes. Precisely, a stopping time
is predictable if the process is almost surely continuous at time
and is totally inaccessible if the underlying Feller process is almost surely discontinuous at
.
As usual, we work with respect to a complete filtered probability space . I now give a statement and proof of the main result of this post. Note that the equivalence of the four conditions below means that any of them can be used as alternative definitions of predictable stopping times. Often, the first condition below is used instead. Stopping times satisfying the definition used in these notes are sometimes called announceable, with the sequence
said to announce
(this terminology is used by, e.g., Rogers & Williams). Stopping times satisfying property 3 below, which is easily seen to be equivalent to 2, are sometimes called fair. Then, the following theorem says that the sets of predictable, fair and announceable stopping times all coincide.
Theorem 1 Let
be a stopping time. Then, the following are equivalent.
.
is a local martingale for all local martingales M.
for all cadlag bounded martingales M.
is predictable.
Before moving on to the proof of the theorem note that, for any stopping time ,
is adapted and left-continuous, hence predictable. Since
, the first statement of the theorem can equivalently by written as
.
Proof: 1 implies 2: As is a bounded predictable process,
is a local martingale. We need to show that
. Although this might seem intuitively obvious, it does require some rather non-trivial properties of the stochastic integral (see the notes below). First,
so N is constant on . Secondly,
, so
for all
. For any time
, note that
vanishes over the interval
whenever
. As previously shown, this means that
whenever
. So,
on
and, hence,
.
2 implies 3: If M is bounded, or just dominated in , then
is an
-dominated local martingale, and hence a proper martingale,
3 implies 4: To show that is predictable, we need to construct a sequence of stopping times
increasing to
such that
whenever
. The idea is simple enough. First define a right-continuous process giving roughly the expected time remaining before
and use the debut theorem to construct
. To do this, start by choosing a continuous bounded and strictly increasing function
. Then define the martingale
Then, tells us (roughly) how much longer we have to wait until time
. In order to be able to choose a cadlag version of M, it is necessary to assume that the filtration is right-continuous, so that
is equal to
. The result does still hold without the assumption of right-continuity and, to be complete, the extension to the general case is given further below. Assuming that M is cadlag, define the following increasing sequence of stopping times,
As , we have that
for all n. Also, by optional sampling,
So, decreases to zero, showing that
tends to zero almost surely. As f was taken to be strictly increasing, this shows that
increases to
. It only remains to show that
is strictly less that
whenever
. The definition of M gives
for all times
. So,
Together with condition 3, which says that , this implies that
is almost surely zero. So,
. However, by construction,
whenever , so,
as required.
4 implies 1: As previously shown, is predictable for all predictable times
and, therefore, so is
. ⬜
An immediate consequence of this result is that the conclusion of the debut theorem can be strengthened in the case of right-continuous and predictable processes. This gives a significant generalization of the much simpler result that hitting times of continuous adapted processes are predictable.
Corollary 2 Let X be a right-continuous and predictable process. Then, for each constant K, the stopping time
is predictable.
Proof: The left-continuous and adapted process is predictable. So,
is predictable and, by Theorem 1, is predictable. ⬜
A process X is locally bounded if there exists a sequence of stopping times increasing to infinity such that the stopped processes
are each uniformly bounded. Continuous processes are easily seen to be locally bounded simply by stopping them as soon as they hit a level
. This generalizes to cadlag predictable processes.
Lemma 3 All cadlag predictable processes are locally bounded.
Proof: Supposing that X is cadlag, define the sequence of stopping times
These are increasing to infinity and, by Corollary 2, are predictable. So, for each m, there is a sequence of stopping times increasing to
such that
whenever
. Then,
are stopping times increasing to infinity. Also,
whenever
. So,
is bounded by n and, hence, X is locally bounded. ⬜
Theorem 1 enables us to state several equivalent conditions for a cadlag adapted process X to be predictable. Note that the process of left-limits is automatically predictable, being left-continuous and adapted. For brevity, I write
for the value of a process at a random time, even though this is not well defined when
. In that case, I take
to be zero whenever
is infinite, so
(setting it to any
-measurable value will not change any of the statements below). I also use
as shorthand for the (progressively measurable and optional) set of times at which X is discontinuous which, more precisely, consists of the
for which
is nonzero. The following notation will be used in the proofs. Given a stopping time
and a set
, the random time
is defined by
It is clear that this defines a stopping time. The statement and proof of the equivalent conditions for a cadlag process to be predictable can now be given.
Lemma 4 If X is a cadlag adapted process then the following are equivalent.
- X is predictable.
is predictable.
is
measurable for all predictable stopping times
, and
(almost surely) whenever
is totally inaccessible.
- there exists a sequence of predictable stopping times
such that
and
is
-measurable for each n.
- there exists a sequence of predictable stopping times
with disjoint graphs (
for
) such that
and
is
-measurable for each n.
Proof: 1 implies 4: Let be a sequence running over the pairs of positive rational numbers, and define the stopping times
| (1) |
Corollary 2 implies that these are predictable. Looking at the individual sample paths of the process, consider a time t for which . Then,
whenever
and
approximates t closely enough from below. It follows that t is contained in the set of times
, so
as required. Also, as X is predictable,
will be
-measurable.
4 implies 5: Let be stopping times satisfying condition 4. As these are predictable and
is
-measurable, the processes
are predictable. So, the set is
-measurable. We can therefore define new predictable stopping times
. By construction, the graphs of
are disjoint and
5 implies 2: If 5 holds then is predictable. So, the same is true of
.
2 implies 1: Simply write X as the sum of two predictable processes.
5 implies 3: We have already shown that 5 implies that X is predictable, so is
-measurable for any stopping time
. Also, for any totally inaccessible stopping time
, then
by definition. So,
is not in
(almost surely) and, therefore,
.
3 implies 4: Defining the sequence of stopping times by (1), we again have
. By the decomposition of stopping times, there exists sets
such that
is accessible and
is totally inaccessible. By condition 3, we have
and, therefore,
is almost surely contained in the graphs of
. By the definition of accessible stopping stopping times, this is contained in the union
of predictable stopping times
. Finally,
is
-measurable by condition 3. ⬜
Applying this characterization to local martingales shows that, for such processes, predictability and continuity are equivalent. In the following, and throughout these notes, statements about the paths of processes are only intended in the almost sure sense. We do not care about what the sample paths look like on zero probability sets.
Lemma 5 A local martingale is predictable if and only if it is continuous.
Proof: As continuous processes are predictable by definition, only the converse needs to be shown. Suppose that M is a predictable local martingale and is a predictable stopping time. Then, for any
, the stopping time
is predictable so, by Theorem 1, the process
is a nonnegative local martingale. Taking
, so that Y is nonnegative and hence a supermartingale, we can take expectations to get
So, almost surely. Also applying this to
shows that
for all predictable stopping times
. However, condition 4 of Lemma 4 shows that the jumps of M are contained in the graphs of a countable set of predictable stopping times, so M is almost surely continuous. ⬜
Note that for a filtration generated by a standard Brownian motion B, the martingale representation theorem implies that all local martingales are continuous, So, the third condition of Theorem 1 is trivially satisfied, giving the remarkable consequence that all stopping times are predictable. More generally, the property that all local martingales are continuous is equivalent to all stopping times being predictable.
Lemma 6 With respect to a complete filtered probability space
, the following are equivalent.
- All stopping times are predictable.
- All cadlag adapted processes are predictable.
- All local martingales are continuous.
Proof: 1 implies 2: Let X be a cadlag adapted process. We can use the characterization of cadlag predictable processes given in the third condition of Lemma 4. It is immediate that (almost surely) for all totally inaccessible
since, by assumption, all stopping times are predictable. Now suppose that
is any stopping time. Then, for
, consider the stopping time
. By the condition, this is predictable, so the process
is predictable. Consequently
is
-measurable. So
and
. So,
is
-measurable for all stopping times
, and X is predictable.
2 implies 3: Any local martingale M is cadlag and adapted, hence is predictable. So, M is continuous by Lemma 5.
3 implies 1: If is a stopping time then any cadlag bounded martingale is continuous, so
. Theorem 1 says that
is predictable. ⬜
As noted above, for the filtration generated by a Brownian motion, the martingale representation theorem has the consequence that all stopping times are predictable.
Corollary 7 Let
be the complete filtration generated by a d-dimensional Brownian motion B. Then, every
-stopping time is predictable.
Rather than using the martingale representation theorem, there is an alternative way to approach Corollary 7. Brownian motion is an example of a Feller process and, in fact, it can be shown that Corollary 7 extends to all continuous Feller processes.
Stopping Times of Feller Processes
For Feller processes it is possible to give a precise characterization of predictable and totally inaccessible stopping times. This follows from the following description of the times at which a local martingale can be discontinuous.
Lemma 8 Let X be a cadlag Feller process and
be its completed natural filtration, and suppose that M is a cadlag
-local martingale.
Then, with probability one,for all times t at which X is continuous.
Proof: By localization, it is enough to prove this result for all cadlag martingales of the form
| (2) |
where is an
-measurable random variable. Let us use
to denote the set of random variables U such that the cadlag martingale defined by (2) is almost-surely continuous wherever X is continuous. We need to show that
is equal to the whole of
. Clearly,
is closed under linear combinations. Furthermore, if
is a sequence in
converging in
to a limit U then the cadlag martingales
converge in the ucp topology to a martingale M which will satisfy (2) and, by ucp convergence, is continuous at all times that
are continuous. So, U is in
. Therefore,
is a closed subspace of
.
Supposing that the Feller process X is defined by the transition function on the lccb space E, consider U of the form
for some
. Then, by the definition of Feller transition functions,
defines a continuous real-valued function on
. Then,
is a martingale which is continuous at all times that X is continuous. So . Next, consider
for a sequence of times
and
, and let M be defined by (2). Then, for each
, there exists a
with
for all (simply take
and
for
). As shown above,
, so M has a cadlag modification on
which is continuous wherever X is continuous. Therefore,
. Finally, by the monotone class theorem, the set of linear combinations of U of this form is dense in
, so
as required. ⬜
Applying Theorem 1 to this result, we obtain the promised characterization of predictable and totally inaccessible stopping times of a Feller process.
Theorem 9 Let X be a cadlag Feller process and
be its completed natural filtration. If
is an
-stopping time then,
is predictable if and only if
almost surely, whenever
.
is totally inaccessible if and only if
almost surely, whenever
.
Proof: As cadlag Feller processes are quasi-left-continuous, if is predictable then
almost surely. Conversely, if
almost surely then, by Lemma 8,
for any cadlag bounded martingale M. Then,
and Theorem 1 says that
is predictable.
For the second statement, suppose that whenever
. Then, as shown above,
(almost surely) for any predictable stopping time
and consequently
. So,
is totally inaccessible. Conversely, suppose that
is totally inaccessible and set
. Then
is a stopping time for which
and, hence, this is predictable so
. Therefore,
whenever
(almost surely). ⬜
One simple but surprising consequence of Theorem 9 is that, for Feller processes, the concepts of predictable and accessible stopping times actually coincide.
Corollary 10 Let
be the complete filtration generated by a Feller process. Then, an
-stopping time is predictable if and only if it is accessible.
Proof: Let X be a cadlag version of the Feller process. If is an accessible stopping time then the second statement of Theorem 9 says that
whenever
. So, by the first statement of Theorem 9,
is predictable. ⬜
For continuous Feller processes, Theorem 9 simply states that, if X is a continuous process, then every stopping time is predictable. This gives the promised extension of Corollary 7 above to all continuous Feller processes.
Corollary 11 Let
be the complete filtration generated by a continuous Feller process. Then, every
-stopping time is predictable.
Non-Right-Continuous Filtrations
In Theorem 1 given above, the right-continuity of the filtration was required in the proof that the third condition implies the fourth. However, right-continuity is not required for the result to hold, and I will give an extension to the non-right-continuous case here. The idea is that we can apply Theorem 1 under the right-continuous filtration and show that both the third and fourth statements of the theorem are unchanged under replacing
by
. First, we re-state the following simple lemma which was proven in the post on the Bichteler-Dellacherie theorem.
Lemma 12 Suppose that M is a cadlag and square-integrable
-martingale. Then, there exists a countable subset
such that
for all
. Furthermore,
is an
-martingale.
We can now give the proof that 3 implies 4 in Theorem 1 without the assumption that the filtration is right-continuous. So, suppose that 3 holds. Then, for any cadlag bounded -martingale M, let S be the countable set of times at which
. Letting
then, as this is an
-martingale, we have
. Next, for any fixed time t, if
is an
-measurable and bounded random variable, then
is easily seen to be a martingale. So, by assumption,
This implies that is in
. Hence,
. Putting this together gives
So, satisfies condition 3 with respect to the right-continuous filtration
. Applying Theorem 1 in this case shows that
is predictable with respect to
. As shown previously, this implies that it is predictable with respect to the original filtration
.
Notes on the Proof of Theorem 1
It is worth pausing here to consider the technical difficulties which had to be overcome in the proof of Theorem 1 above. The equivalence of statements 2 and 3 is easy to show without applying any advanced techniques, as is the fact that 4 implies 1. The proof that the third statement implies the fourth (fair stopping times are announceable) was a bit trickier to show but, still, constructing the sequence of stopping times announcing was achieved without too much difficulty, although extending the result to non-right-continuous filtrations gets a bit messy.
The proof that the first statement implies the second (predictable times are fair) can be the most technically demanding part of the proof of Theorem 1, so I will discuss some of the various approaches in this section. We managed to deal with this very efficiently in this post by making use of the identity
| (3) |
and using the fact that stochastic integration preserves the local martingale property. Although (3) seems intuitively obvious by thinking about the integral in a pathwise sense, and is easy to prove for Riemann-Stieltjes integrals, it is much harder to show that the stochastic integral satisfies this identity. It does not follow easily from the defining properties of the stochastic integral — namely the bounded or dominated convergence theorem and the explicit expression for elementary integrands. Instead, we had to make use of the result that stochastic integrals coincide on any event for which the integrands coincide. This does seem like a simple enough statement, which we would expect to hold. However, the proof of this result required showing that semimartingales remain as semimartingales when the filtration is enlarged by adding a set to . This, in turn, required the characterization of semimartingales in terms of boundedness in probability of elementary integrals, which was rather demanding to prove, and was restated as part of the Bichteler-Dellacherie theorem. So, the seemingly simple statement that 1 implies 2 in Theorem 1 actually required some rather advanced stochastic calculus, and we would have been hard-pressed to give a short proof in these notes before the stochastic integral had been developed.
It is interesting to compare with the proof given in Rogers & Williams (Diffusions, Markov Processes, and Martingales, Volume 2, §VI.16.4-13), where the implication is denoted by P ⇒ F (predictable implies fair). They open with the following paragraph.
“Proof that P ⇒ F. If you wish to understand the subject properly, you need to understand the proof of the section theorems, and this proof that P ⇒ F, much of which is based on §IV.76 of Dellacherie and Meyer, is a good introduction to the methods required. We did try for some time to find a quick proof that P ⇒ F, but though many `proofs’ would immediately spring to the mind of anyone familiar with stochastic-integral theory, they all presuppose that P ⇒ A (although it sometimes takes a little thought to spot exactly where!).”
It seems likely that the proofs mentioned that would immediately spring to mind are those based on identity (3). If it is assumed that the stopping time is announceable, then this identity is easy to prove (hence, the presupposition that P ⇒ A). Fortunately, the approach that has been taken in these notes means that we were able to prove (3) without any such presupposition, so we could give a quick stochastic integration based proof that
implies that
is fair.
An alternative proof of the result is to apply the section theorems, as suggested by Rogers & Williams in the quote above. The section theorems are very powerful results on which much of the historical development of stochastic calculus depended, although their proofs are rather demanding and are based on predictive set theory and analytic sets. The predictable section theorem in particular implies that if is a predictable set then there exist predictable stopping times
with
tending to
. This implies that
is predictable (i.e., that it is announceable), giving a proof that statement 1 implies 4 in Theorem 1. The proof given by Rogers & Williams does not use the section theorems themselves, but does involve ideas from their proofs, and is essentially based on the Choquet capacity theorem. However, in these notes I have taken a different approach to stochastic calculus, attempting to develop the stochastic integral in a more direct and slightly more intuitive way which avoids any use of the section theorems.
There do exist other methods of proving that stopping times satisfying are fair which avoid the use both of identity (3) and of the section theorems. For example, Metivier & Pellaumail (Stochastic Integration, 1980) give a relatively direct proof of the Doob-Meyer decomposition theorem without invoking any major machinery which, in particular, implies that every integrable increasing predictable process A and bounded cadlag martingale M with
satisfies the identity
Applying this to the predictable process implies that
is fair. More details on this will be mentioned in a later post on compensators.
Hi,
So first,
In your proof of theorem 1, in the “2 implies 3” part, you mention the fact that if a local martinglae is
is  -dominated then it is a true martingale. As I couldn’t find in your notes this precise statement, would it be right to say the following ?
-dominated then it is a true martingale. As I couldn’t find in your notes this precise statement, would it be right to say the following ?
As -domination entails that
-domination entails that  is locally integrable (by hypotheses
is locally integrable (by hypotheses  such that
such that  ), which in turn implies that
), which in turn implies that  is of class DL (see lemma 9 in your post "Localization"), and so the local martingale
is of class DL (see lemma 9 in your post "Localization"), and so the local martingale  is a true martingale (by theorem 1 in your post on "Local Martingales"). Moreover here
is a true martingale (by theorem 1 in your post on "Local Martingales"). Moreover here  is uniformly integrable (or U.I.) as a
is uniformly integrable (or U.I.) as a  -dominated family of random variable is U.I.. So you can say that
-dominated family of random variable is U.I.. So you can say that 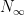 exists almost surely and use it in the equallity following the statement about the martingale property of
exists almost surely and use it in the equallity following the statement about the martingale property of  .
.
Maybe a more elementary proof exists but I missed it, otherwise if the result exists in your blog you consider hyperlinking it with the claim.
Best regards
I think you’ve more or less got the argument, except, for the locally integrable part. Local integrability is too week to imply that it is a true martingale. In fact, all local martingales are locally integrable anyway. Lemma 9 in the post mentioned only implies that it is locally of class (DL), not actually of class DL itself.
Instead, if M is L1-dominated (by X), then the set of random variables {XT: T is a finite stopping time} must also be dominated by X, so uniformly integrable. Hence, M is of class (D) (so also of class DL). Now use Theorem 1 from the post on local martingales. And, class (D) implies that it is UI, so N∞ exists by martingale convergence, and the martingale property E[Nt|Fs] = Ns also holds for t = ∞.
I tend not to spell out all the small steps once it gets down to just what is relatively standard manipulations that occur all over the place. Maybe in some places these steps are a bit big, depending on how familiar or not you are with this stuff. If I can make it easier to follow without making arguments which I think should be short and direct seem long and complicated, then I will (when I have time to go back and clean up posts).
Hi, first thank you for responding so fast,
I got your point.
Regarding spelling out small steps, well I think it depends on the size of one’s legs, and some kind of human factor is involved in the process.
I know there is always a trade-off between synthetized fancy style exposition of a mathematical proof and elementary exhaustive but tedious rigourous demonstration, as “élégance” is an determinant factor in the process.
At this game, your are particularly gifted in my opinion but as it is generally hard for high skilled people to get what is hard to get for not as smart guys, I only point out from time to time those steps which are sometimes too high for me.
Best regards
Hi,
Second,
I think there is a typo in “3 implies 4”. You wrote :
Where I think it is :
Shortly after that, using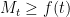 you show that :
you show that :
Besides, I don’t see why then condition 3 is required to ensure that is almost surely 0.
is almost surely 0.
Best regards
Yes, regarding the typo, you’re correct. I fixed this, thanks.
Condition 3 is certainly required to ensure that ΔM is almost surely zero, otherwise it would prove that every stopping time is predictable!
What happens if you try the same argument for a non-predictable stopping time is that ΔM can be strictly negative. Then, with positive probability, you have for some n, and then
for some n, and then 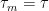 for m ≥ n, so the sequence
for m ≥ n, so the sequence  does not announce
does not announce  strictly from below.
strictly from below.
Hi
I got it thanks
Best regards
Hi,
For the proof in lemma 3, unless I missed something I think that the argument is a little too fast as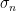 is non deacreasing but can be forced through (not so) appropriate choice of
is non deacreasing but can be forced through (not so) appropriate choice of  to make
to make 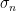 to be “constant” (meaning that is the same random variable over and over),so a proper choice of the index
to be “constant” (meaning that is the same random variable over and over),so a proper choice of the index  (depending on
(depending on  and
and  ) has to be done, or alternatively some condition over the construction of
) has to be done, or alternatively some condition over the construction of  has to be imposed for every
has to be imposed for every  , for example
, for example  almost surely (I think this is possible with no arm).
almost surely (I think this is possible with no arm).
In the proof of lemma 4, for the sake of exhaustivity you might also consider hyperlinking in the end of the “1 implies 4” argument, the sentence :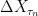 will be
will be  -measurable,” to lemma 1 of the post “Sigma Algebras at a Stopping Time” (appears also in the “5 implies 3” argument).
-measurable,” to lemma 1 of the post “Sigma Algebras at a Stopping Time” (appears also in the “5 implies 3” argument).
“Also, as X is predictable,
Hope this is not too much, but as I come almost at the end of my lecture of your notes the rythm of those comments should slow down soon dramatically.
Best regards
Regarding Lemma 3. Yes, there was a mistake, which I’ve fixed. The correct choice of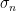 is actually much easier than you might expect when you first think about it (I think this is what I had in my head when I wrote this post, but it came out wrong).
is actually much easier than you might expect when you first think about it (I think this is what I had in my head when I wrote this post, but it came out wrong).
I added the links you suggested.
And, no, its not too much at all! I like having the feedback on these notes. Any comments which help me improve them is much appreciated. Besides, I never normally know if anyone has actually read through the details of the more in-depth proofs. You’ve almost read through all of my notes? That’s pretty good going!
Hi,
Yes I must admit I did read almost all of them and had a great pleasure doing so, and as you don’t feel annoyed by my comments I will keep up making some when I feel I have to.
Best regards
Hi,
I’ve got a question. I take a continuous process and it’s natural filtration. Is it possible to show, that all optional processes are predictable wrt to my filtration?
Best regards
hi, i am asking what is application of indicator function on stopping time and why also indicator function is used on writing jump process
I am not sure precisely what your question is, but is the process equal to zero before stopping time
is the process equal to zero before stopping time  and equal to 1 at and after the stopping time, so is a very basic jump process.
and equal to 1 at and after the stopping time, so is a very basic jump process.
Hi,
Is Theorem 9 remain valid for time-inhomgeneous Markov proccess with a feller evolution systems?
I’m not sure what you mean by ‘Feller evolution systems’
Hi,
Thank you for the excellent blogs!
Question: Why in Lemma 3, we cannot use $\tau^m$ as the localizing sequence?