In this post I’ll give a proof of Rao’s decomposition for quasimartingales. That is, every quasimartingale decomposes as the sum of a submartingale and a supermartingale. Equivalently, every quasimartingale is a difference of two submartingales, or alternatively, of two supermartingales. This was originally proven by Rao (Quasi-martingales, 1969), and is an important result in the general theory of continuous-time stochastic processes.
As always, we work with respect to a filtered probability space . It is not required that the filtration satisfies either of the usual conditions — the filtration need not be complete or right-continuous. The methods used in this post are elementary, requiring only basic measure theory along with the definitions and first properties of martingales, submartingales and supermartingales. Other than referring to the definitions of quasimartingales and mean variation given in the previous post, there is no dependency on any of the general theory of semimartingales, nor on stochastic integration other than for elementary integrands.
Recall that, for an adapted integrable process X, the mean variation on an interval is
where the supremum is taken over all elementary processes with
. Then, X is a quasimartingale if and only if
is finite for all positive reals t. It was shown that all supermartingales are quasimartingales with mean variation given by
| (1) |
Rao’s decomposition can be stated in several different ways, depending on what conditions are required to be satisfied by the quasimartingale X. As the definition of quasimartingales does differ between texts, there are different versions of Rao’s theorem around although, up to martingale terms, they are equivalent. In this post, I’ll give three different statements with increasingly stronger conditions for X. First, the following statement applies to all quasimartingales as defined in these notes. Theorem 1 can be compared to the Jordan decomposition, which says that any function with finite variation on bounded intervals can be decomposed as the difference of increasing functions or, equivalently, of decreasing functions. Replacing finite variation functions by quasimartingales and decreasing functions by supermartingales gives the following.
Theorem 1 (Rao) A process X is a quasimartingale if and only if it decomposes as
(2) for supermartingales Y and Z. Furthermore,
- this decomposition can be done in a minimal sense, so that if
is any other such decomposition then
is a supermartingale.
- the inequality
(3) holds, with equality for all
if and only if the decomposition is minimal.
- the minimal decomposition is unique up to a martingale. That is, if
are two such minimal decompositions, then
is a martingale.
By replacing Y and Z by –Z and –Y, this theorem can alternatively be written in terms of decompositions into the difference of submartingales, which is how it is sometimes stated. I stick to using supermartingales in this post, in order to be consistent with the alternative statements of Rao’s theorem given below. Also, in the statement above, the processes Y and Z occurring in the decomposition are not required to be cadlag. This is because we are not requiring X to satisfy any pathwise properties or putting any restrictions on the underlying filtration. However, as we will show in Lemma 5 below, if X is cadlag and the filtration satisfies the usual conditions then Y and Z do have cadlag modifications.
In the statement of Theorem 1, the fact that inequality (3) holds for all such decompositions follows immediately from identity (1) for the mean variation of a supermartingale together with the fact that is subadditive on the space of integrable processes. However, the fact that equality holds for the minimal decomposition is more advanced, and this will be left until the proof of the theorem given further below. Also, the statement that the minimal decomposition is unique up to a martingale follows easily from the definitions. If
were two minimal decompositions then, by definition, both
and
are supermartingales, so
is a martingale.
One possible problem with the decomposition in Theorem 1 is that it is not unique. We only obtain uniqueness up to a martingale term. However, by placing slightly stronger conditions on X, it is possible to obtain a unique minimal decomposition. The mean variation of an integrable process X on was defined as
Here, the supremum is taken over all elementary processes with
. In particular, for a nonnegative supermartingale X, applying (1) to
gives
| (4) |
with equality if and only if in
as t goes to infinity.
The following version of Rao’s decomposition can be compared to the statement that any function with bounded total variation decomposes as
, where c is constant and
are nonnegative functions decreasing to zero. Similarly as above, the statement of Theorem 2 is obtained by replacing functions of bounded total variation by processes with
, replacing the constant term by a martingale, and replacing decreasing functions by supermartingales. One technical point should be made before stating this theorem. As I am not assuming that any of the processes have nice pathwise properties, such as being cadlag, it does not make sense to consider two processes X and Y to be equal only if they are equal up to evanescence (i.e., that
simultaneously for all t, with probability 1). This is not determined by the joint distributions of X and Y at finite sets of times, and need not even be a measurable property. Instead, I consider X and Y to be equal if the weaker condition
for each time t is satisified. Similarly, a process X will be called nonnegative if
for each time t.
Theorem 2 (Rao) An integrable adapted process X satisfies
if and only if it decomposes as
(5) for a martingale M and nonnegative supermartingales Y, Z. Furthermore,
- this decomposition can be done in a minimal sense, so that if
is any other such decomposition then
and
are nonnegative supermartingales.
- the inequality
(6) holds, with equality if and only if the decomposition is minimal.
- the minimal decomposition is unique in the sense that, if
is any other such minimal decomposition then,
,
and
(almost surely) for each
.
- in the minimal decomposition, the limits
hold almost surely and in
, and the martingale M is almost surely zero at each time if and only if
in
.
As we will see in Lemma 4 below, the supermartingales Y,Z in minimal decomposition (5) do agree with those in (2) up to martingale terms. The proof of Theorem 2 will be left until later on in this post. Note, however that inequality (6) is an immediate consequence of (4) for the mean variation of a supermartingale together with the fact that is a subadditive function on the integrable processes and that the martingale M has zero mean variation. Uniqueness of the minimal decomposition is also immediate. If
was any other minimal decomposition then, by definition, both
and
are nonnegative, so
. Similarly,
and, hence,
.
Let us now move on to the third version of Rao’s decomposition, which gives a unique minimal decomposition, but does not involve the additional martingale term as in (5). For any integrable adapted process X, we defined the following increasing function of t,
Then, the mean variation of X on is,
where the supremum is taken over all elementary process with index set
and satisfying
. In the case where X is not integrable, then
is defined to be infinite. For nonnegative supermartingales,
independently of t. So, every nonnegative supermartingale satisfies
| (7) |
We now state the third version of Rao’s decomposition, which applies to all integrable adapted processes with finite.
Theorem 3 (Rao) An adapted process X satisfies
if and only if it decomposes as
(8) for nonnegative supermartingales Y and Z. Furthermore,
- this decomposition can be done in a minimal sense, so that if
is any other such decomposition then
is a nonnegative supermartingale.
- the inequality
(9) holds, with equality if and only if the decomposition is minimal.
- the minimal decomposition is unique in the sense that, if
are two such minimal decompositions, then
and
(almost surely) for each
.
Note that inequality (9) is a straightforward consequence of identity (7) for the mean variation of a nonnegative supermartingale together with the fact that is subadditive. Also, as in the statement of Theorem 2, uniqueness of the minimal decomposition follows immediately from the definition of minimality.
We can show that the supermartingales Y and Z in each of the three alternative statements of Rao’s decomposition do agree up to a martingale term.
Lemma 4 Let X be a quasimartingale and
be a decomposition as the difference of supermartingales which is minimal in the sense of Theorem 1.
If the minimal decomposition (5) exists then
and
are martingales. Similarly, if the minimal decomposition (8) exists then
and
are martingales.
Proof: If is the minimal decomposition (8) then, it needs to be shown that this is also minimal in the sense of Theorem 1, so that uniqueness of minimal decompositions will imply that
is a martingale.
By definition of minimality in (8), if for nonnegative supermartingales
, then
is a supermartingale. It just needs to be shown that this still holds when the processes are not assumed to be nonnegative. However, in that case, we can stop
at any fixed time T to define new supermartingales
Then, for all
, from which we have
for all . So
and, similarly,
are nonnegative supermartingales. Furthermore, the equality
implies that
. By minimality in decomposition (8),
is a (nonnegative) supermartingale over . As the final term on the right hand side is a martingale and T was arbitrary, it follows that
is a supermartingale and, similarly, so is
, as was required.
Next, suppose that the minimal decomposition (5) exists. Then, setting , minimality implies that if
is any other decomposition as the difference of nonnegative supermartingales then,
are nonnegative supermartingales. So, the decomposition
is also minimal in the sense of Theorem 3 and, by what we have already shown above, is also minimal in the sense of Theorem 1. So,
is a minimal decomposition of X as the difference of supermartingales in the sense of Theorem 1 and, hence,
is a martingale. Similarly,
is a martingale. ⬜
Finally, before moving on to the proof of Rao’s decomposition, we show that the supermartingales Y and Z do indeed have a cadlag modification under suitable conditions.
Lemma 5 Suppose that X is a cadlag process and that the filtration satisfies the usual conditions.
Whenever either of the minimal decompositions (2), (5) and (8) exist then, the supermartingales Y and Z have a cadlag modification.
Proof: First, as the underlying filtration is assumed to satisfy the usual conditions, every martingale has a cadlag modification. As Lemma 4 says that the minimal decompositions (5) and (8) reduce to (2) up to a martingale term, it is enough to just consider decomposition (2).
So, suppose that is a minimal decomposition of X as the difference of supermartingales, and let T be any fixed time. Choose a sequence of times
strictly decreasing to T. Then, as in the proof of existence of cadlag modifications of submartingales and supermartingales, the limits
exist in . Furthermore, as the filtration satisfies the usual conditions,
and
are
-measurable. The supermartingale property implies that
and, similarly, . We now define new supermartingales by subtracting out the jump at time T,
These are indeed supermartingales. If then, for any
,
Taking the limit as n goes to infinity gives,
This inequality also follows immediately from the supermartingale property for Y in the case that T is not contained in the interval . So
and, similarly,
are supermartingales. As X is right-continuous,
By minimality of the decomposition, this implies that is a supermartingale and, hence,
As is nonnegative, this shows that
and, hence, Y is right-continuous in probability. Therefore, it has a cadlag modification. Similarly, Z has a cadlag modification. ⬜
Proof of Rao’s Decomposition
In discrete time, Rao’s decomposition is particularly easy to prove. So, I’ll start by describing the decomposition in this setting and, then, generalize to continuous time by taking limits along a sequence of partitions.
Consider any integrable adapted process with time index t running through a finite set
, and define the nonnegative adapted processes
Then,
So, let us suppose now that , in which case we obtain the decomposition
. Next, the inequalities
show that Y and Z are supermartingales. This decomposition is also minimal in the sense that if is any other such decomposition for supermartingales
and
then,
and
are supermartingales.
The final equality follows from the fact that and
are supermartingales and, hence, the conditional expectations on the right hand side of the inequality are nonpositive. Rearranging this slightly as
shows that is a supermartingale and, similarly for
. If is furthermore assumed that
are nonnegative then,
So, and, similarly,
are nonnegative. The mean variation of X can be written as
Now, let us turn our attention to continuous-time processes by approximation with the discrete-time case described above. Suppose that X is an integrable adapted process with time index . We extend this to a process on
by setting
. A partition
of the interval
is defined to be an increasing sequence of times
.
Now, using the partition , define the processes
,
By comparing with the discrete-time case above, we see that, restricted to the times in ,
and
are supermartingales satisfying
. Also, for any time t not in P, the definition of
and
given above is unchanged if we refine P by adding t. So, the identity
holds (almost surely) at each time t.
Define the mean variation on P as
and recall that is the supremum of
taken over all partitions P of
. Taking the limit of this decomposition along a suitable sequence of decompositions gives the continuous-time version of Rao’s decomposition stated in Theorem 3.
Lemma 6 Suppose that
, and let
be a sequence of partitions of
such that
as m goes to infinity. Then, the limits
exist in
independently of the choice of partitions, and,
and
are nonnegative supermartingales satisfying
Furthermore, if
is any other decomposition of X as the difference of nonnegative supermartingales, then
and
are also nonnegative supermartingales.
Proof: First consider two partitions P and Q of such that Q is a refinement of Q. As described above, restricted to the times in Q,
and
are supermartingales satisfying the identity
. In particular,
and
are supermartingales when restricted to the times in P. So, by the minimality of the decomposition
, the processes
and
are nonnegative supermartingales at the times in P. For each time t in P this gives,
Note, also, that adding any fixed time t to the partition P does not affect the definitions of given above. So, this inequality holds for all
.
Now consider any two partitions P and Q of . Then, letting R be a refinement of both P and Q.
In particular if is a sequence of partitions with
then this shows that
and
is Cauchy in
. It also shows that if
is any other such sequence then
and
tends to zero in
. So, the limits defining
and
do indeed exist independently of the specific choice of partitions
used. Also, taking limits in
,
as required.
It remains to show that Y and Z are supermartingales. Fixing times , we can refine the partitions
to obtain new partitions
containing these times. As shown above,
and
will be nonnegative supermartingales at the times in
, so that
By the first part of the lemma, proven above, this shows that converges to
in
for all times u. As
is a supermartingale at the times in
, taking limits in
gives the inequality
So Y and, similarly, Z are supermartingales.
Finally, suppose that for nonnegative supermartingales
,
. By the minimality of the discrete-time decomposition,
and
are nonnegative supermartingales at the times in
. Again, taking limits in
, this shows that
and
are nonnegative supermartingales. ⬜
It is now a simple matter of applying Lemma 6 to prove Rao’s decomposition in the form of Theorem 3.
Proof of Theorem 3: First, existence of the decomposition (8) gives
So, finiteness of is a necessary condition, and inequality (9) holds. Conversely, suppose that
is finite. Lemma 6 states the existence of a decomposition
for nonnegative supermartingales
, which is minimal in the required sense and satisfies
So, equality does indeed hold in (9) for the minimal decomposition.
Finally, suppose that is any decomposition of X as the difference of supermartingales such that equality holds in (9) and that
is the minimal decomposition. Then,
,
are nonnegative supermartingales and,
So, ,
and the decomposition is minimal as claimed. ⬜
We now move on to proving the alternative statement of Rao’s decomposition given in Theorem 2. This can be done in a similar way to above, by first explicitly writing out the decomposition in discrete time and them taking the limit along a sequence of partitions. However, as we have already given a proof of Theorem 3, we will instead take the approach of reducing decomposition (5) to (8) by subtracting out a martingale term. The statement that X can be decomposed as the sum of a martingale and a term tending to zero in is sometimes referred to as the Riesz decomposition of X.
Lemma 7 Let X be an integrable process such that
. Then, for each
, the limit
exists in
. Furthermore, M is a martingale and
in
as
.
Proof: Consider any times and sequence
. Then, by the definition of
in terms of partitions,
Taking the supremum over all such finite sequences for the gives
Using to denote
, then
is a martingale and, hence,
is a submartingale. So, for
,
which tends to zero as S,T go to infinity. So, is Cauchy in
as
and, hence,
exists in
. Also, as it is an
limit of martingales, M is itself a martingale.
Finally, for ,
Letting T increase to infinity,
This tends to zero as S goes to infinity, so tends to zero in
. ⬜
We can now prove Theorem 2 by subtracting out a martingale term as in Lemma 7 and applying the decomposition already proven above.
Proof of Theorem 2: If decomposition (5) exists then,
So, inequality (6) holds and is a necessary condition. Conversely, suppose that
is finite. Then, Lemma 7 says that there exists a martingale M such that
in
as t goes to infinity. Setting
,
So, Theorem 3 applies, and there exists a minimal decomposition for supermartingales Y and Z. This gives
as in decomposition (5) and, by (9),
In particular, this gives
As they are nonnegative, this implies that and
tend to zero in
as
. Now, suppose that
is any other decomposition for martingale
and nonnegative supermartingales
. Then,
expresses as the difference of supermartingales. By Lemma 4, minimality of the decomposition
implies that
and
are supermartingales. In particular,
is a supermartingale so, for any
,
As in
, this shows that
and, similarly,
are nonnegative. So, the decomposition is minimal as claimed. We also see that
and, similarly,
in
as
. Also,
in
, so if M is identically zero then
and, conversely, if
in
then,
Finally, suppose that is any decomposition for martingale M and nonnegative supermartingales Y,Z such that equality holds in (6), and that
is the minimal decomposition. Then,
,
are nonnegative supermartingales and,
So, ,
, and the decomposition is minimal. ⬜
Finally, we move on to proving Rao’s decomposition in the form of Theorem 1. This can be done by applying the decomposition (8) over an increasing sequence of bounded intervals, and patching these together to obtain (2) for arbitrary quasimartingales.
Proof of Theorem 1: First, as supermartingales are quasimartingales and linear combinations of quasimartingales are quasimartingales, if X is the difference of supermartingales then it is a quasimartingale.
Conversely, let X be a quasimartingale. Let us start by assuming that the minimal decomposition (2) does indeed exist, and that is any fixed time. The stopped process
is a difference of supermartingales. If
is any other such decomposition then,
are again supermartingales satisfying . Therefore,
and
are supermartingales and, stopping at time T,
and
are also supermartingales. This shows that the decomposition
is also minimal, so stopping the processes at deterministic times preserves minimal decompositions.
Now, suppose that X is any quasimartingale and, again, that is any fixed time. Then, the stopped process
satisfies
So, Theorem 3 applies to , and we can let
be a decomposition which is minimal in the sense of (8). By Lemma 4, it is also minimal in the sense of Theorem 1. So, the minimal decomposition does always exist if we stop the process at a finite time. Furthermore, as equality holds in (9),
So, equality holds in (3) and, as the minimal decomposition is unique up to a martingale term, it holds for any minimal decomposition.
Next, let be a sequence of deterministic times increasing to infinity and, for each n, let
be a minimal decomposition as the difference of supermartingales. As minimal decompositions are preserved by stopping at deterministic times, is also a minimal decomposition. Then, as minimal decompositions are unique up to a martingale, this implies that
is a martingale. We can define new minimal decompositions by setting
,
and, for each
,
As is a martingale on
, we also have
on this range. Also,
and, as
,
are martingales, these are also minimal decompositions. As
and
for all
, we can set
For each t, this is just the limit of a constant sequence once . Then,
are supermartingales with
. Suppose that
is any other such decomposition. By stopping at time
and using the fact that
is a minimal decomposition then, it follows that
are supermartingales. As this holds for each n,
is a supermartingale and the decomposition is minimal.
Finally, suppose that is any decomposition as a difference of supermartingales such that equality holds in (3) and that
is a minimal decomposition. Then,
is independent of t. As are supermartingales their expectations are nonincreasing functions of t and, hence, are constant in t. As a supermartingale with constant expectation is a martingale, this shows that
is a martingale, so the decomposition is indeed minimal. ⬜
Hi, I want to use some theorems in your blogs, but how I add the references of these theorems? Could you tell me a name of a book or something? Thank you very much
Hi, I have a personal question. Do you ever find it hard to balance piracy and general marauding with your mathematics career? How do you strike a good pirate-math balance?
Thank you very much,
Kevin Stangl
Avast ye! The last landlubber to ask personal questions like ye had to walk the plank and pay a visit to Davy Jones’ Locker. Aaaarrrrgggghhhh! Yo ho ho, and all that.
Hi George! First of all thank you for your blog, it is very complete and precise.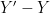 is nonnegative, are you assuming that
is nonnegative, are you assuming that  (and similarly
(and similarly 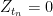 )? Above you said “let us assume
)? Above you said “let us assume  ” which is weaker than saying
” which is weaker than saying  and
and 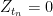 but otherwise I don’t see how you could prove that
but otherwise I don’t see how you could prove that ![\mathbb{E}\left[Y^\prime_{t_n}-Y_{t_n}|\mathcal{F}_{t_k}\right]=0](https://s0.wp.com/latex.php?latex=%5Cmathbb%7BE%7D%5Cleft%5BY%5E%5Cprime_%7Bt_n%7D-Y_%7Bt_n%7D%7C%5Cmathcal%7BF%7D_%7Bt_k%7D%5Cright%5D%3D0&bg=ffffff&fg=000000&s=0&c=20201002) . If you assume
. If you assume  (let’s say by construction) then you can say
(let’s say by construction) then you can say ![\mathbb{E}\left[Y^\prime_{t_n}-Y_{t_n}|\mathcal{F}_{t_k}\right]\geq 0](https://s0.wp.com/latex.php?latex=%5Cmathbb%7BE%7D%5Cleft%5BY%5E%5Cprime_%7Bt_n%7D-Y_%7Bt_n%7D%7C%5Cmathcal%7BF%7D_%7Bt_k%7D%5Cright%5D%5Cgeq+0&bg=ffffff&fg=000000&s=0&c=20201002) , since
, since  is nonnegative, and this is sufficient to prove that
is nonnegative, and this is sufficient to prove that 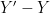 is nonnegative.
is nonnegative.
I have a doubt about one step of the proof of Rao’s decomposition. It refers to the discrete time, when you are proving the “minimality” of the decomposition, and in particular when you want to prove that
Am I right or am I missing something?
Cheers,
Alessandro Milazzo
Hi Alessandro. I assume you are talking about the argument immediately following the heading “Proof of Rao’s decomposition”. I don’t need to assume anything about because I explicitly define it. The fact that
because I explicitly define it. The fact that  follows from the definition (note that the summation on the rhs of the definition for
follows from the definition (note that the summation on the rhs of the definition for  has no terms). You are correct to bring up the equality
has no terms). You are correct to bring up the equality ![\mathbb{E}[Y^\prime_{t_n}-Y_{t_n}\,\vert\mathcal{F}_{t_k}]=0](https://s0.wp.com/latex.php?latex=%5Cmathbb%7BE%7D%5BY%5E%5Cprime_%7Bt_n%7D-Y_%7Bt_n%7D%5C%2C%5Cvert%5Cmathcal%7BF%7D_%7Bt_k%7D%5D%3D0&bg=ffffff&fg=000000&s=0&c=20201002) though. This is a mistake and should be an inequality, as you point out, which is all that is required by the argument anyway.
though. This is a mistake and should be an inequality, as you point out, which is all that is required by the argument anyway.
I’ll update to fix this point and to clarify when I have some time.
Many thanks!
George
You are right, George!
Thanks again,
Alessandro
Hi George, I have a question about the construction of Rao’s decomposition in discrete time. In the proof you assume that $X_{t_n}=0$. What if the process you’re considering does not satisfy this property? How would you construct the Rao’s decomposition in that case? My intuitive guess is to construct a process $\tilde{X}$ which is the same as $X$ but extended at a further time $\tilde{X}_{t_{n+1}}=0$. Then, define $Y$ and $Z$ as you did where now the sums go up to $n+1$ instead of $n$. This seems to work to me. Is that the right procedure?
Thanks,
Alessandro