The Minimum and Maximum of Brownian motion

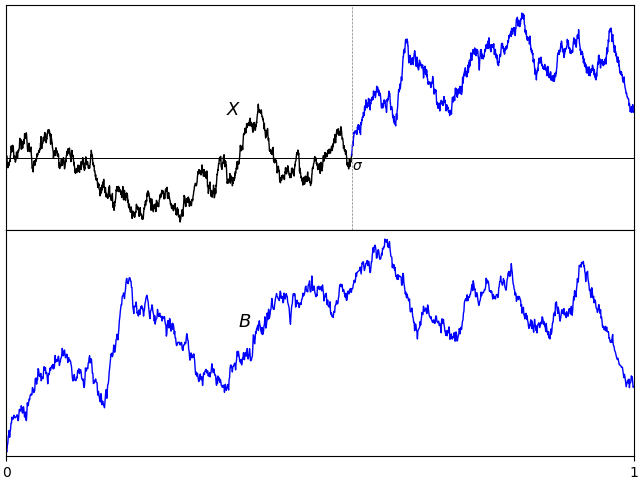
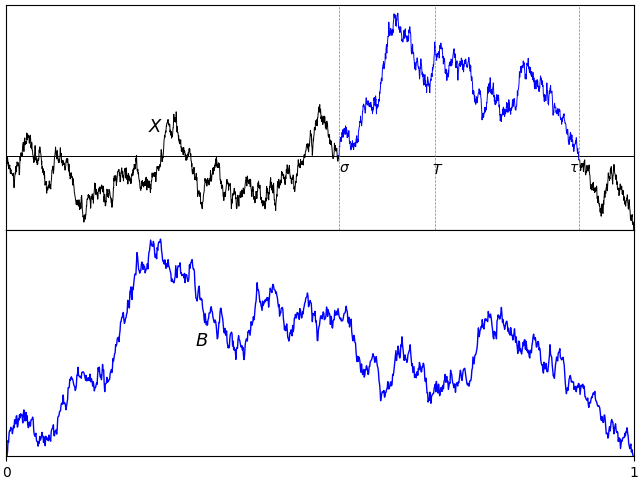
If X is standard Brownian motion, what is the distribution of its absolute maximum |X|_t^∗ = sup_s ≤ t|X_s| over a time interval [0, t]? Previously, I looked at how the reflection principle can be used to determine that the maximum X_t^∗ = sup_s ≤ tX_s has the same distribution as |X_t|. This is not the same thing as the maximum of the absolute value though, which is a more difficult quantity to describe. As a first step, |X|_t^∗ is clearly at least as large as X_t^∗ from which it follows that it stochastically dominates |X_t|.

I would like to go further and precisely describe the distribution of |X|_t^∗. What is the probability that it exceeds a fixed positive level a? For this to occur, the suprema of both X and –X must exceed a. Denoting the minimum and maximum by

$\displaystyle \begin{aligned} &X_t^m=\inf_{s\le t}X_s,\\ &X_t^M=\sup_{s\le t}X_s, \end{aligned}$

then |X|_t^∗ is the maximum of X_t^M and –X_t^m. I have switched notation a little here, and am using X^M to denote what was previously written as X^∗. This is just to use similar notation for both the minimum and maximum. Using inclusion-exclusion, the probability that the absolute maximum is greater than a level a is,

$\displaystyle \begin{aligned} {\mathbb P}(\lvert X\rvert_t^* > a)={} & {\mathbb P}(X_t^M > a)+{\mathbb P}(X_t^m < -a)\\ & -{\mathbb P}(X_t^M > a{\rm\ and\ }X_t^m < -a). \end{aligned}$

As X_t^M has the same distribution as |X_t| and, by symmetry, so does –X^m, we obtain

$\displaystyle {\mathbb P}(\lvert X\rvert_t^* > a)=4{\mathbb P}(X_t > a)-{\mathbb P}(X_t^M > a{\rm\ and\ }X_t^m < -a).$

This hasn’t really answered the question. All we have done is to re-express the probability in terms of both the minimum and maximum being beyond a level. For large values of a it does, however, give a good approximation. The probability of the Brownian motion reaching a large positive value a and then dropping to the large negative value –a will be vanishingly small, so the final term in the identity above can be neglected. This gives an asymptotic approximation as a tends to infinity,

$\displaystyle \begin{aligned} {\mathbb P}(\lvert X\rvert_t^* > a) &\sim 4{\mathbb P}(X_t > a)\\ &\sim\sqrt{\frac{8t}{\pi a^2}}e^{-\frac{a^2}{2t}}. \end{aligned}$

(1)

The last expression here is just using the fact that X_t is centered Gaussian with variance t and applying a standard approximation for the cumulative normal distribution function.

For small values of a, approximation (1) does not work well at all. We know that the left-hand-side should tend to 1, whereas 4ℙ(X_t > a) will tend to 2, and the final expression diverges. In fact, it can be shown that

$\displaystyle {\mathbb P}(\lvert X\rvert_t^* < a)\sim\frac{4}{\pi}e^{-\frac{t\pi^2}{8a^2}}$

(2)

as a → 0. I gave a direct proof in this math.stackexchange answer. In this post, I will look at how we can compute joint distributions of the minimum, maximum and terminal value of Brownian motion, from which limits such as (2) will follow. Continue reading “The Minimum and Maximum of Brownian motion” →

The Brownian Drawdown Process

The drawdown of a stochastic process is the amount that it has dropped since it last hit its maximum value so far. For process X with running maximum X^∗_t = sup_s ≤ tX_s, the drawdown is thus X^∗_t – X_t, which is a nonnegative process. This is as in figure 1 below.

Brownian motion drawdown — Figure 1: Brownian motion and its drawdown process

The previous post used the reflection principle to show that the maximum of a Brownian motion has the same distribution as its terminal absolute value. That is, X^∗_t and |X_t| are identically distributed.

For a process X started from zero, its maximum and drawdown can be written as X^∗_t – X₀ and X^∗_t – X_t. Reversing the process in time across the interval [0, t] will exchange these values. So, reversing in time and translating so that it still starts from zero will exchange the maximum value and the drawdown. Specifically, write

$\displaystyle Y_s = X_{t-s} - X_t$

for time index 0 ≤ s ≤ t. The maximum of Y is equal to the drawdown of X,

$\displaystyle Y^*_t = X^*_t-X_t.$

If X is standard Brownian motion then so is Y, since the independent normal increments property for Y follows from that of X. As already stated, the maximum Y^∗_t = X^∗_t – X_t has the same distribution as the absolute value |Y_t|= |X_t|. So, the drawdown has the same distribution as the absolute value at each time.

Lemma 1 If X is standard Brownian motion, then X^∗_t – X_t has the same distribution as |X_t| at each time t ≥ 0.

Continue reading “The Brownian Drawdown Process” →

Brownian Meanders

Having previously looked at Brownian bridges and excursions, I now turn to a third kind of process which can be constructed either as a conditioned Brownian motion or by extracting a segment from Brownian motion sample paths. Specifically, the Brownian meander, which is a Brownian motion conditioned to be positive over a unit time interval. Since this requires conditioning on a zero probability event, care must be taken. Instead, it is cleaner to start with an alternative definition by appropriately scaling a segment of a Brownian motion.

For a fixed positive times T, consider the last time σ before T at which a Brownian motion X is equal to zero,

$\displaystyle \sigma=\sup\left\{t\le T\colon X_t=0\right\}.$

(1)

On interval [σ, T], the path of X will start from 0 and then be either strictly positive or strictly negative, and we may as well restrict to the positive case by taking absolute values. Scaling invariance says that c^-1/2X_ct is itself a standard Brownian motion for any positive constant c. So, scaling the path of X on [σ, 1] to the unit interval defines a process

$\displaystyle B_t=(T-\sigma)^{-1/2}\lvert X_{\sigma+t(T-\sigma)}\rvert.$

(2)

over 0 ≤ t ≤ 1; This starts from zero and is strictly positive at all other times.

Brownian meander construction — Figure 2: Constructing a Brownian meander

Scaling invariance shows that the law of the process B does not depend on the choice of fixed time T The only remaining ambiguity is in the choice of the fixed time T.

Lemma 1 The distribution of B defined by (2) does not depend on the choice of the time T > 0.

Proof: Consider any other fixed positive time T̃, and use the construction above with T̃, σ̃, B̃ in place of T, σ, B respectively. We need to show that B̃ and B have the same distribution. Using the scaling factor S = T̃/T, then X′_t = S^-1/2X_tS is a standard Brownian motion. Also, σ′= σ̃/S is the last time before T at which X′ is zero. So,

$\displaystyle \tilde B_t=(T-\sigma')^{-1/2}\lvert X'_{\sigma'+t(T-\sigma')}\rvert$

has the same distribution as B. ⬜

This leads to the definition used here for Brownian meanders.

Definition 2 A continuous process {B_t}_{t ∈ [0, 1]} is a Brownian meander if and only it has the same distribution as (2) for a standard Brownian motion X and fixed time T > 0.

In fact, there are various alternative — but equivalent — ways in which Brownian excursions can be defined and constructed.

As a scaled segment of a Brownian motion before a time T and after it last hits 0. This is definition 2.
As a Brownian motion conditioned on being positive. See theorem 4 below.
As a segment of a Brownian excursion. See lemma 5.
As the path of a standard Brownian motion starting from its minimum, in either the forwards or backwards direction. See theorem 6.
As a Markov process with specified transition probabilities. See theorem 9 below.
As a solution to an SDE. See theorem 12 below.

Continue reading “Brownian Meanders” →

Brownian Excursions

A normalized Brownian excursion is a nonnegative real-valued process with time ranging over the unit interval, and is equal to zero at the start and end time points. It can be constructed from a standard Brownian motion by conditioning on being nonnegative and equal to zero at the end time. We do have to be careful with this definition, since it involves conditioning on a zero probability event. Alternatively, as the name suggests, Brownian excursions can be understood as the excursions of a Brownian motion X away from zero. By continuity, the set of times at which X is nonzero will be open and, hence, can be written as the union of a collection of disjoint (and stochastic) intervals (σ, τ).

In fact, Brownian motion can be reconstructed by simply joining all of its excursions back together. These are independent processes and identically distributed up to scaling. Because of this, understanding the Brownian excursion process can be very useful in the study of Brownian motion. However, there will by infinitely many excursions over finite time periods, so the procedure of joining them together requires some work. This falls under the umbrella of ‘excursion theory’, which is outside the scope of the current post. Here, I will concentrate on the properties of individual excursions.

In order to select a single interval, start by fixing a time T > 0. As X_T is almost surely nonzero, T will be contained inside one such interval (σ, τ). Explicitly,

$\displaystyle \begin{aligned} &\sigma=\sup\left\{t\le T\colon X_t=0\right\},\\ &\tau=\inf\left\{t\ge T\colon X_t=0\right\}, \end{aligned}$

(1)

so that σ < T < τ < ∞ almost surely. The path of X across such an interval is t ↦ X_σ + t for time t in the range [0, τ - σ]. As it can be either nonnegative or nonpositive, we restrict to the nonnegative case by taking the absolute value. By invariance, S^-1/2X_tS is also a standard Brownian motion, for each fixed S > 0. Using a stochastic factor S = τ – σ, the width of the excursion is normalised to obtain a continuous process {B_t}_{t ∈ [0, 1]} given by

$\displaystyle B_t=(\tau-\sigma)^{-1/2}\lvert X_{\sigma+t(\tau-\sigma)}\rvert.$

(2)

By construction, this is strictly positive over 0 < t < 1 and equal to zero at the endpoints t ∈ {0, 1}.

Figure 2: Constructing a Brownian excursion

The only remaining ambiguity is in the choice of the fixed time T.

Lemma 1 The distribution of B defined by (2) does not depend on the choice of the time T > 0.

Proof: This follows from scaling invariance of Brownian motion. Consider any other fixed positive time T̃, and use the construction above with T̃, σ̃, τ̃, B̃ in place of T, σ, τ, B respectively. We need to show that B̃ and B have the same distribution. Using the scaling factor S = T̃/T, then X′_t = S^-1/2X_tS is a standard Brownian motion. Also, σ′= σ̃/S and τ′= τ̃/S are random times given in the same way as σ and τ, but with the Brownian motion X′ in place of X in (1). So,

$\displaystyle \tilde B_t=(\tau^\prime-\sigma^\prime)^{-1/2}\lvert X^\prime_{\sigma^\prime+t(\tau^\prime-\sigma^\prime)}\rvert$

has the same distribution as B. ⬜

This leads to the definition used here for Brownian excursions.

Definition 2 A continuous process {B_t}_{t ∈ [0, 1]} is a Brownian excursion if and only it has the same distribution as (2) for a standard Brownian motion X and time T > 0.

In fact, there are various alternative — but equivalent — ways in which Brownian excursions can be defined and constructed.

As a normalized excursion away from zero of a Brownian motion. This is definition 2.
As a normalized excursion away from zero of a Brownian bridge. This is theorem 6.
As a Brownian bridge conditioned on being nonnegative. See theorem 9 below.
As the sample path of a Brownian bridge, translated so that it has minimum value zero at time 0. This is a very interesting and useful method of directly computing excursion sample paths from those of a Brownian bridge. See theorem 12 below, sometimes known as the Vervaat transform.
As a Markov process with specified transition probabilities. See theorem 15 below.
As a transformation of Bessel process paths, see theorem 16 below.
As a Bessel bridge of order 3. This can be represented either as a Bessel process conditioned on hitting zero at time 1., or as the vector norm of a 3-dimensional Brownian bridge. See lemma 17 below.
As a solution to a stochastic differential equation. See theorem 18 below.

Continue reading “Brownian Excursions” →

Brownian Bridge Fourier Expansions

Figure 1: Sine series approximations to a Brownian bridge

Brownian bridges were described in a previous post, along with various different methods by which they can be constructed. Since a Brownian bridge on an interval ${[0,T]}$ is continuous and equal to zero at both endpoints, we can consider extending to the entire real line by partitioning the real numbers into intervals of length T and replicating the path of the process across each of these. This will result in continuous and periodic sample paths, suggesting another method of representing Brownian bridges. That is, by Fourier expansion. As we will see, the Fourier coefficients turn out to be independent normal random variables, giving a useful alternative method of constructing a Brownian bridge.

There are actually a couple of distinct Fourier expansions that can be used, which depends on precisely how we consider extending the sample paths to the real line. A particularly simple result is given by the sine series, which I describe first. This is shown for an example Brownian bridge sample path in figure 1 above, which plots the sequence of approximations formed by truncating the series after a small number of terms. This tends uniformly to the sample path, although it is quite slow to converge as should be expected when approximating such a rough path by smooth functions. Also plotted, is the series after the first 100 terms, by which time the approximation is quite close to the target. For simplicity, I only consider standard Brownian bridges, which are defined on the unit interval ${[0,1]}$ . This does not reduce the generality, since bridges on an interval ${[0,T]}$ can be expressed as scaled versions of standard Brownian bridges.

Theorem 1 A standard Brownian bridge B can be decomposed as

$\displaystyle B_t=\sum_{n=1}^\infty\frac{\sqrt2Z_n}{\pi n}\sin(\pi nt)$ (1)

over ${0\le t\le1}$ , where ${Z_1,Z_2,\ldots}$ is an IID sequence of standard normals. This series converges uniformly in t, both with probability one and in the ${L^p}$ norm for all ${1\le p < \infty}$ .

Continue reading “Brownian Bridge Fourier Expansions” →

Brownian Bridges

A Brownian bridge can be defined as standard Brownian motion conditioned on hitting zero at a fixed future time T, or as any continuous process with the same distribution as this. Rather than conditioning, a slightly easier approach is to subtract a linear term from the Brownian motion, chosen such that the resulting process hits zero at the time T. This is equivalent, but has the added benefit of being independent of the original Brownian motion at all later times.

Lemma 1 Let X be a standard Brownian motion and ${T > 0}$ be a fixed time. Then, the process

$\displaystyle B_t = X_t - \frac tTX_T$ (1)

over ${0\le t\le T}$ is independent from ${\{X_t\}_{t\ge T}}$ .

Proof: As the processes are joint normal, it is sufficient that there is zero covariance between them. So, for times ${s\le T\le t}$ , we just need to show that ${{\mathbb E}[B_sX_t]}$ is zero. Using the covariance structure ${{\mathbb E}[X_sX_t]=s\wedge t}$ we obtain,

$\displaystyle {\mathbb E}[B_sX_t]={\mathbb E}[X_sX_t]-\frac sT{\mathbb E}[X_TX_t]=s-\frac sTT=0$

as required. ⬜

This leads us to the definition of a Brownian bridge.

Definition 2 A continuous process ${\{B_t\}_{t\in[0,T]}}$ is a Brownian bridge on the interval ${[0,T]}$ if and only it has the same distribution as ${X_t-\frac tTX_T}$ for a standard Brownian motion X.

In case that ${T=1}$ , then B is called a standard Brownian bridge.

There are actually many different ways in which Brownian bridges can be defined, which all lead to the same result.

As a Brownian motion minus a linear term so that it hits zero at T. This is definition 2.
As a Brownian motion X scaled as ${tT^{-1/2}X_{T/t-1}}$ . See lemma 9 below.
As a joint normal process with prescribed covariances. See lemma 7 below.
As a Brownian motion conditioned on hitting zero at T. See lemma 14 below.
As a Brownian motion restricted to the times before it last hits zero before a fixed positive time T, and rescaled to fit a fixed time interval. See lemma 15 below.
As a Markov process. See lemma 13 below.
As a solution to a stochastic differential equation with drift term forcing it to hit zero at T. See lemma 18 below.

There are other constructions beyond these, such as in terms of limits of random walks, although I will not cover those in this post. Continue reading “Brownian Bridges” →

Independence of Normals

A well known fact about joint normally distributed random variables, is that they are independent if and only if their covariance is zero. In one direction, this statement is trivial. Any independent pair of random variables has zero covariance (assuming that they are integrable, so that the covariance has a well-defined value). The strength of the statement is in the other direction. Knowing the value of the covariance does not tell us a lot about the joint distribution so, in the case that they are joint normal, the fact that we can determine independence from this is a rather strong statement.

Theorem 1 A joint normal pair of random variables are independent if and only if their covariance is zero.

Proof: Suppose that X,Y are joint normal, such that ${X\overset d= N(\mu_X,\sigma^2_X)}$ and ${Y\overset d=N(\mu_Y,\sigma_Y^2)}$ , and that their covariance is c. Then, the characteristic function of ${(X,Y)}$ can be computed as

$\displaystyle \begin{aligned} {\mathbb E}\left[e^{iaX+ibY}\right] &=e^{ia\mu_X+ib\mu_Y-\frac12(a^2\sigma_X^2+2abc+b^2\sigma_Y^2)}\\ &=e^{-abc}{\mathbb E}\left[e^{iaX}\right]{\mathbb E}\left[e^{ibY}\right] \end{aligned}$

for all ${(a,b)\in{\mathbb R}^2}$ . It is standard that the joint characteristic function of a pair of random variables is equal to the product of their characteristic functions if and only if they are independent which, in this case, corresponds to the covariance c being zero. ⬜

To demonstrate necessity of the joint normality condition, consider the example from the previous post.

Example 1 A pair of standard normal random variables X,Y which have zero covariance, but ${X+Y}$ is not normal.

As their sum is not normal, X and Y cannot be independent. This example was constructed by setting ${Y={\rm sgn}(\lvert X\rvert -K)X}$ for some fixed ${K > 0}$ , which is standard normal whenever X is. As explained in the previous post, the intermediate value theorem ensures that there is a unique value for K making the covariance ${{\mathbb E}[XY]}$ equal to zero. Continue reading “Independence of Normals” →

Multivariate Normal Distributions

I looked at normal random variables in an earlier post but, what does it mean for a sequence of real-valued random variables ${X_1,X_2,\ldots,X_n}$ to be jointly normal? We could simply require each of them to be normal, but this says very little about their joint distribution and is not much help in handling expressions involving more than one of the ${X_i}$ at once. In case that the random variables are independent, the following result is a very useful property of the normal distribution. All random variables in this post will be real-valued, except where stated otherwise, and we assume that they are defined with respect to some underlying probability space ${(\Omega,\mathcal F,{\mathbb P})}$ .

Lemma 1 Linear combinations of independent normal random variables are again normal.

Proof: More precisely, if ${X_1,\ldots,X_n}$ is a sequence of independent normal random variables and ${a_1,\ldots,a_n}$ are real numbers, then ${Y=a_1X_1+\cdots+a_nX_n}$ is normal. Let us suppose that ${X_k}$ has mean ${\mu_k}$ and variance ${\sigma_k^2}$ . Then, the characteristic function of Y can be computed using the independence property and the characteristic functions of the individual normals,

$\displaystyle \begin{aligned} {\mathbb E}\left[e^{i\lambda Y}\right] &={\mathbb E}\left[\prod_ke^{i\lambda a_k X_k}\right] =\prod_k{\mathbb E}\left[e^{i\lambda a_k X_k}\right]\\ &=\prod_ke^{-\frac12\lambda^2a_k^2\sigma_k^2+i\lambda a_k\mu_k} =e^{-\frac12\lambda^2\sigma^2+i\lambda\mu} \end{aligned}$

where we have set ${\mu_k=\sum_ka_k\mu_k}$ and ${\sigma^2=\sum_ka_k^2\sigma_k^2}$ . This is the characteristic function of a normal random variable with mean ${\mu}$ and variance ${\sigma^2}$ . ⬜

The definition of joint normal random variables will include the case of independent normals, so that any linear combination is also normal. We use use this result as the defining property for the general multivariate normal case.

Definition 2 A collection ${\{X_i\}_{i\in I}}$ of real-valued random variables is multivariate normal (or joint normal) if and only if all of its finite linear combinations are normal.

Continue reading “Multivariate Normal Distributions” →

The Riemann Zeta Function and Probability Distributions

Phi and Psi densities — Figure 1: Probability densities used to extend the zeta function

The famous Riemann zeta function was first introduced by Riemann in order to describe the distribution of the prime numbers. It is defined by the infinite sum

$\displaystyle \begin{aligned} \zeta(s) &=1+2^{-s}+3^{-s}+4^{-s}+\cdots\\ &=\sum_{n=1}^\infty n^{-s}, \end{aligned}$

(1)

which is absolutely convergent for all complex s with real part greater than one. One of the first properties of this is that, as shown by Riemann, it extends to an analytic function on the entire complex plane, other than a simple pole at ${s=1}$ . By the theory of analytic continuation this extension is necessarily unique, so the importance of the result lies in showing that an extension exists. One way of doing this is to find an alternative expression for the zeta function which is well defined everywhere. For example, it can be expressed as an absolutely convergent integral, as performed by Riemann himself in his original 1859 paper on the subject. This leads to an explicit expression for the zeta function, scaled by an analytic prefactor, as the integral of ${x^s}$ multiplied by a function of x over the range ${ x > 0}$ . In fact, this can be done in a way such that the function of x is a probability density function, and hence expresses the Riemann zeta function over the entire complex plane in terms of the generating function ${{\mathbb E}[X^s]}$ of a positive random variable X. The probability distributions involved here are not the standard ones taught to students of probability theory, so may be new to many people. Although these distributions are intimately related to the Riemann zeta function they also, intriguingly, turn up in seemingly unrelated contexts involving Brownian motion.

In this post, I derive two probability distributions related to the extension of the Riemann zeta function, and describe some of their properties. I also show how they can be constructed as the sum of a sequence of gamma distributed random variables. For motivation, some examples are given of where they show up in apparently unrelated areas of probability theory, although I do not give proofs of these statements here. For more information, see the 2001 paper Probability laws related to the Jacobi theta and Riemann zeta functions, and Brownian excursions by Biane, Pitman, and Yor. Continue reading “The Riemann Zeta Function and Probability Distributions” →

Manipulating the Normal Distribution

The normal (or Gaussian) distribution is ubiquitous throughout probability theory for various reasons, including the central limit theorem, the fact that it is realistic for many practical applications, and because it satisfies nice properties making it amenable to mathematical manipulation. It is, therefore, one of the first continuous distributions that students encounter at school. As such, it is not something that I have spent much time discussing on this blog, which is usually concerned with more advanced topics. However, there are many nice properties and methods that can be performed with normal distributions, greatly simplifying the manipulation of expressions in which it is involved. While it is usually possible to ignore these, and instead just substitute in the density function and manipulate the resulting integrals, that approach can get very messy. So, I will describe some of the basic results and ideas that I use frequently.

Throughout, I assume the existence of an underlying probability space ${(\Omega,\mathcal F,{\mathbb P})}$ . Recall that a real-valued random variable X has the standard normal distribution if it has a probability density function given by,

$\displaystyle \varphi(x)=\frac1{\sqrt{2\pi}}e^{-\frac{x^2}2}.$

For it to function as a probability density, it is necessary that it integrates to one. While it is not obvious that the normalization factor ${1/\sqrt{2\pi}}$ is the correct value for this to be true, it is the one fact that I state here without proof. Wikipedia does list a couple of proofs, which can be referred to. By symmetry, ${-X}$ and ${X}$ have the same distribution, so that they have the same mean and, therefore, ${{\mathbb E}[X]=0}$ .

The derivative of the density function satisfies the useful identity

$\displaystyle \varphi^\prime(x)=-x\varphi(x).$

(1)

This allows us to quickly verify that standard normal variables have unit variance, by an application of integration by parts.

$\displaystyle \begin{aligned} {\mathbb E}[X^2] &=\int x^2\varphi(x)dx\\ &= -\int x\varphi^\prime(x)dx\\ &=\int\varphi(x)dx-[x\varphi(x)]_{-\infty}^\infty=1 \end{aligned}$

Another identity satisfied by the normal density function is,

$\displaystyle \varphi(x+y)=e^{-xy - \frac{y^2}2}\varphi(x)$

(2)

This enables us to prove the following very useful result. In fact, it is difficult to overstate how helpful this result can be. I make use of it frequently when manipulating expressions involving normal variables, as it significantly simplifies the calculations. It is also easy to remember, and simple to derive if needed.

Theorem 1 Let X be standard normal and ${f\colon{\mathbb R}\rightarrow{\mathbb R}_+}$ be measurable. Then, for all ${\lambda\in{\mathbb R}}$ ,

$\displaystyle \begin{aligned} {\mathbb E}[e^{\lambda X}f(X)] &={\mathbb E}[e^{\lambda X}]{\mathbb E}[f(X+\lambda)]\\ &=e^{\frac{\lambda^2}{2}}{\mathbb E}[f(X+\lambda)]. \end{aligned}$ (3)

Continue reading “Manipulating the Normal Distribution” →

	Anonymous on Spitzer’s Formula
	Anonymous on Spitzer’s Formula
	Anonymous on Brownian Bridges
	Anonymous on Spitzer’s Formula
	Anonymous on Spitzer’s Formula
	Anonymous on Spitzer’s Formula
	Anonymous on Spitzer’s Formula
	Anonymous on Spitzer’s Formula
	Anonymous on Spitzer’s Formula
	Anonymous on Spitzer’s Formula