A martingale is a stochastic process which stays the same, on average. That is, the expected future value conditional on the present is equal to the current value. Examples include the wealth of a gambler as a function of time, assuming that he is playing a fair game. The canonical example of a continuous time martingale is Brownian motion and, in discrete time, a symmetric random walk is a martingale. As always, we work with respect to a filtered probability space . A process
is said to be integrable if the random variables
are integrable, so that
.
Definition 1 A martingale,
, is an integrable process satisfying
for all
.
A closely related concept is that of a submartingale, which is a process which increases on average. This could represent the wealth of a gambler who is involved in games where the odds are in his favour. Similarly, a supermartingale decreases on average.
Definition 2 A process
is a
- submartingale if it is integrable and
for all
.
- supermartingale if it is integrable and
for all
.
This terminology can perhaps be a bit confusing, but it is related to the result that if is an n-dimensional Brownian motion and
then
is a submartingale or supermartingale when
is a subharmonic or, respectively, a superharmonic function.
Clearly, is a submartingale if and only if
is a supermartingale, and is a martingale if and only if it is both a submartingale and a supermartingale.
Lemma 3 If
is a martingale and
is a convex function such that
is integrable, then,
is a submartingale.
Proof: This is a direct consequence of Jensen’s inequality,
⬜
In particular, if is any
-integrable martingale for
then
is a submartingale. A similar result holds for submartingales, although the additional hypothesis that the function is increasing is required.
Lemma 4 Suppose that
is a submartingale and
is an increasing convex function such that
is integrable. Then,
is a submartingale.
Proof: Again, Jensen’s inequality gives the result,
where the final inequality follows from the monotonicity of . ⬜
So, the positive part of a submartingale
is itself a submartingale.
Elementary integrals
Martingales and submartingales are especially well behaved under stochastic integration. An elementary or elementary predictable process is of the form
| (1) |
for , times
,
-measurable random variable
and
-measurable random variables
. Alternatively,
is elementary if it is left-continuous and adapted, and there are times
such that
is constant on each of the intervals
and zero on
. In particular, these are predictable processes and, in fact, generate the predictable sigma-algebra. It is also clear that the set of elementary processes is closed under linear combinations and products, and
is elementary for any elementary
and measurable function
.
Stochastic integrals of such elementary processes can be written out explicitly. The integral of the process given by (1) with respect to a stochastic process is
The integral over a finite range is,
Note that, for this expression to make sense, it is only strictly necessary for to be elementary for each
. Equivalently,
is given by expression (1) for
and
. Alternatively,
is left-continuous and adapted, and there is a sequence of times
such that it is constant over each of the intervals
.
Letting run over the domain
, the integral
defines a new process. I shall often write
, dropping the limits, to express the stochastic integral as a process. This can equivalently be written in the differential form
, which is just a shorthand for the integral expression.
These elementary integrals satisfy some basic properties which follow directly from the definitions. Linearity in both the integrand and integrator
is clear. Furthermore, associativity holds. If
are elementary and
then
In differential notation, this is simply . Stopping an integral process at a random time
is the same as stopping the integrator,
| (2) |
The full theory of stochastic calculus extends these elementary integrals to arbitrary predictable integrands. However, just the elementary case defined above is enough to get going with. First, considering expectations of stochastic integrals leads to the following alternative definition of martingales and submartingales.
Theorem 5 An adapted integrable process
is
- a martingale if and only if
for all bounded elementary processes
.
- a submartingale if and only if
(3) for all nonnegative bounded elementary processes
.
Proof: It is enough to prove the second statement, because the first one follows immediately from applying this to both and
. So, suppose that
is a submartingale. An elementary and nonnegative elementary process
can be written in the form (1) for
nonnegative. Then,
Conversely, suppose that inequality (3) holds. Choosing any and
. The process
is elementary and
Choosing ,
Any non-positive random variable whose expectation is zero must itself be equal to zero, almost surely. So, as required. ⬜
Elementary integrals preserve the martingale property.
Lemma 6 Let
be a process and
be a bounded elementary process. Define
. Then
- If
is a martingale then so is
.
- If
is a submartingale and
is non-negative then
is a submartingale.
Proof: The first statement follows from the second applied to both and
. So, it is enough to consider the case where
is a submartingale. If
is a nonnegative elementary process then associativity of the integral gives
This inequality follows from the previous lemma and, again by the previous lemma, it shows that is a submartingale. ⬜
Finally, optional stopping of martingales follows from the properties of elementary integrals. This extends the martingale property to random stopping times. The value of an arbitrary process at the random time
need not be well behaved, or even measurable, unless we restrict to nice versions of processes. So, for this post, we shall call a stopping time simple if it only takes finitely many values in
. If
is a bounded simple stopping time taking values in
then the process
is elementary and, furthermore, equation (2) can be extended to give
The optional stopping theorem states that the class of martingales is closed under stopping at arbitrary stopping times.
Lemma 7 Let
be a martingale (resp. submartingale, supermartingale) and
be a simple stopping time. Then, the stopped process
is also a martingale (resp. submartingale, supermartingale).
Proof: This follows from applying Lemma 6 to the following identity
⬜
Hello George, I really like this blog.
Do you know whether the Theorem 5 result![E\left[\int_0^t \xi\,dW\right]=0](https://s0.wp.com/latex.php?latex=E%5Cleft%5B%5Cint_0%5Et+%5Cxi%5C%2CdW%5Cright%5D%3D0&bg=ffffff&fg=000000&s=0&c=20201002) , for
, for 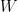 a martingale, can be extended to a more general class of stochastic processes
a martingale, can be extended to a more general class of stochastic processes 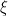 ? Maybe something like
? Maybe something like 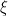 being integrable, adapted to the natural filtration of
being integrable, adapted to the natural filtration of 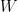 , a.s. cadlag and a.s. uniformly bounded on
, a.s. cadlag and a.s. uniformly bounded on ![[0,t]](https://s0.wp.com/latex.php?latex=%5B0%2Ct%5D&bg=ffffff&fg=000000&s=0&c=20201002) ?
?
Yes you can, but you probably want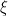 to at least be predictable, and you need to first develop some theory in order to give meaning to the integral, and impose sufficient conditions on the sample paths of W. The point of this post is that we do not require any prior knowledge of stochastic integration nor that we have well-behaved versions (such as right-continuous) of the process W.
to at least be predictable, and you need to first develop some theory in order to give meaning to the integral, and impose sufficient conditions on the sample paths of W. The point of this post is that we do not require any prior knowledge of stochastic integration nor that we have well-behaved versions (such as right-continuous) of the process W.
Hi George when you define simple stopping time at the bottom, do you take t_0 = 0? In the sum there should be a t_0. But in this case what happens if \tau takes 0? By definition you have it should be t_1 = 0. Also in Lemma 7, why is there X_0 in addition to the integral for X^\tau?
Yes, I took t_0=0. I edited the post to clarify. It should be fine when tau is zero.
In lemma 7 I added on X_0 because, by definition, the integral over an interval (0,t] is X_t-X_0, so need to add this term back on.
Hi, in the proof of Theorem 5, the last part of the first equation reads![\displaystyle \sum_{k=1}^n{\mathbb E}\left[Z_k({\mathbb E}[X_{t_k}\mid\mathcal{F}_{s_k}]-X_s)\right]\ge 0](https://s0.wp.com/latex.php?latex=%5Cdisplaystyle+%5Csum_%7Bk%3D1%7D%5En%7B%5Cmathbb+E%7D%5Cleft%5BZ_k%28%7B%5Cmathbb+E%7D%5BX_%7Bt_k%7D%5Cmid%5Cmathcal%7BF%7D_%7Bs_k%7D%5D-X_s%29%5Cright%5D%5Cge+0&bg=ffffff&fg=000000&s=0&c=20201002) . Shouldn’t the last
. Shouldn’t the last 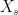 be
be 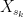 ?
?
Fixed. Thanks!