On The Integral ∫I(W ≥ 0)dW

In this post I look at the integral X_t = ∫₀^t 1_{W≥0} dW for standard Brownian motion W. This is a particularly interesting example of stochastic integration with connections to local times, option pricing and hedging, and demonstrates behaviour not seen for deterministic integrals that can seem counter-intuitive. For a start, X is a martingale so has zero expectation. To some it might, at first, seem that X is nonnegative and — furthermore — equals W ∨ 0. However, this has positive expectation contradicting the first property. In fact, X can go negative and we can compute its distribution. In a Twitter post, Oswin So asked about this very point, showing some plots demonstrating the behaviour of the integral.

simulation of X — Figure 1: Numerically evaluating ∫¹₀ 1_{W≥0} dW

We can evaluate the integral as X_t = W_t ∨ 0 – 12 L_t⁰ where L_t⁰ is the local time of W at 0. The local time is a continuous increasing process starting from 0, and only increases at times where W = 0. That is, it is constant over intervals on which W is nonzero. The first term, W_t ∨ 0 has probability density p(x) equal to that of a normal density over x > 0 and has a delta function at zero. Subtracting the nonnegative value L⁰_t spreads out the density of this delta function to the left, leading to the odd looking density computed numerically in So’s Twitter post, with a peak just to the left of the origin and dropping instantly to a smaller value on the right. We will compute an exact form for this probability density but, first, let’s look at an intuitive interpretation in the language of option pricing.

Consider a financial asset such as a stock, whose spot price at time t is S_t. We suppose that the price is defined at all times t ≥ 0 and has continuous sample paths. Furthermore, suppose that we can buy and sell at spot any time with no transaction costs. A call option of strike price K and maturity T pays out the cash value (S_T - K)₊ at time T. For simplicity, assume that this is ‘out of the money’ at the initial time, meaning that S₀ ≤ K.

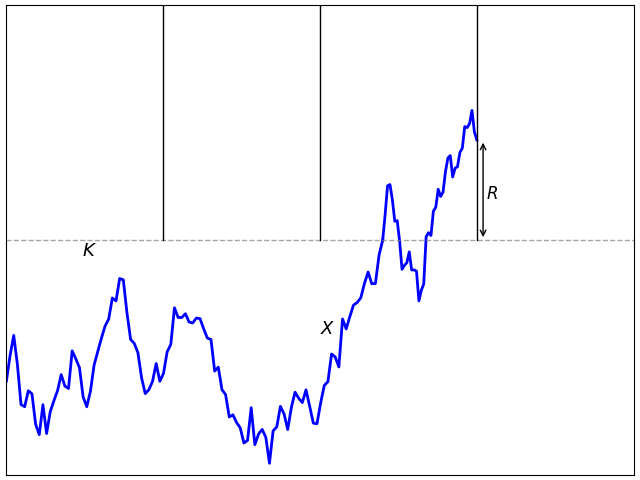
The idea of option hedging is, starting with an initial investment, to trade in the stock in such a way that at maturity T, the value of our trading portfolio is equal to (S_T - K)₊. This synthetically replicates the option. A naive suggestion which is sometimes considered is to hold one unit of stock at all times t for which S_t ≥ K and zero units at all other times.The profit from such a strategy is given by the integral X_T = ∫₀^T 1_{S≥K} dS. If the stock only equals the strike price at finitely many times then this works. If it first hits K at time s and does not drop back below it on interval (s, t) then the profit at t is equal to the amount S_t – K that it has gone up since we purchased it. If it drops back below the strike then we sell at K for zero profit or loss, and this repeats for subsequent times that it exceeds K. So, at time T, we hold one unit of stock if its value is above K for a profit of S_T – K and zero units for zero profit otherwise. This replicates the option payoff.

The idea described works if S_T hits the strike K at a finite set of times,and also if the path of S_t has finite variation, in which case Lebesgue-Stieltjes integration gives X_T = (S_T - K)₊. It cannot work for stock prices though! If it did, then we have a trading strategy which is guaranteed to never lose money but generates profits on the positive probability event that S_T > K. This is arbitrage, generating money with zero risk, which should be impossible.

What goes wrong? First, Brownian motion does not have sample paths with finite variation and will not hit a level finitely often. Instead, if it reaches K then it hits the level uncountably often. As our simple trading strategy would involve buying and selling infinitely often, it is not so easy. Instead, we can approximate by a discrete-time strategy and take the limit. Choosing a finite sequence of times 0 = t₀ < t₁ < ⋯< t_n = T, the discrete approximation is to hold one unit of the asset over the interval (t_i, t_i+1] if S_{t_i} ≥ K and zero units otherwise.

The discrete strategy involves buying one unit of the asset whenever its price reaches K at one of the discrete times and selling whenever it drops back below. This replicates the option payoff, except for the fact then when we buy above K we effectively overpay by amount S_{t_i} – K and, when we sell below K, we lose K – S_{t_i}. This results in some slippage from not being able to execute at the exact level,

$\displaystyle A_T=\sum_{i=1}^{n}1_{\{S_{t_{i-1}} < K\le S_{t_i}{\rm\ or\ }S_{t_{i-1}}\ge K > S_{t_i}\}}\lvert S_{t_i}-K\rvert.$

So, our simple trading strategy generates profit (S_T - K)₊ – A_T, missing the option value by amount A_T. In the limit as n goes to infinity with time step size going to zero, the slippage A_T does not go to zero. For equally spaced times, It can be shown that the number of times that spot crosses K is of order √n, and each of these times generates slippage of order 1/√n on average. So, in the limit, A_T does not vanish and, instead, converges on a positive value equal to half the local time L_T^K.

Figure 2: Naive option hedge with slippage

Figure 2 shows the situation, with the slippage A shown on the same plot (using K as the zero axis, so they are on the same scale). We can just take K = 0 for an asset whose spot price can be positive or negative. Then, with S = W, our integral X_T = ∫₀^T 1_{W≥0} dW is the same as the payoff from the naive option hedge, or (S_T)₊ minus slippage L⁰_T/2.

Now lets turn to a computation of the probability density of X_T = W_T ∨ 0 – L_T⁰/2. By the scaling property of Brownian motion, the distribution of X_T/√T does not depend on T, so we take T = 1 without loss of generality. The first trick to this is to make use of the fact that, if M_t = sup_s≤tW_s is the running maximum then (|W_t|, L_t⁰) has the same joint distribution as (M_t - W_t, M_t). This immediately tells us that L₁⁰ has the same distribution as M₁ which, by the reflection principle, has the same distribution as |W₁|. Using

$\displaystyle \varphi(x)=\frac1{\sqrt{2\pi}}e^{-\frac12x^2}$

for the standard normal density, this shows that the local time L₁⁰ has probability density 2φ(x) over x > 0.

Next, as flipping the sign W does not impact either |W₁| or L₁⁰, sgn(W₁) is independent of these. On the event W₁ < 0 we have X₁ = –L₁⁰/2 which has density 4φ(2x) over x < 0. On the event W₁ > 0, we have X₁ = |W₁|-L₁⁰/2, which has the same distribution as M₁/2 – W₁.

To complete the computation of the probability density of X₁, we need to know the joint distribution of M₁ and W₁, which can be done as described in the post on the reflection principle. The probability that W₁ is in an interval of width δx about a point x and that M₁ > y, for some y > x is, by reflection, equal to the probability that W₁ is in an interval of width δx about the point 2y – x. This has probability φ(2y - x)δx and, by differentiating in y, gives a joint probability density of 2φ′(x - 2y) for (W₁, M₁).

The expectation of f(X₁) for bounded measurable function f can be computed by integrating over this joint probability density.

$\displaystyle \begin{aligned} {\mathbb E}[f(X_1)\vert\;W_1 > 0] &={\mathbb E}[f(M_1/2-W_1)]\\ &=2\int_{-\infty}^\infty\int_{x_+}^\infty f(y/2-x)\varphi'(x-2y)\,dydx\\ &=4\int_{-\infty}^\infty\int_{(-x)\vee(-x/2)}^\infty f(z)\varphi'(-3x-4z)\,dzdx\\ &=4\int_{-\infty}^\infty\int_{(-z)\vee(-2z)}^\infty f(z)\varphi'(-3x-4z)\,dxdz\\ &=\frac43\int_{-\infty}^\infty f(z)\varphi(2z)\,dz+\frac43\int_0^\infty f(z)\varphi(z)\,dz. \end{aligned}$

The substitution z = y/2 – x was applied in the inner integral, and the order of integration switched. The probability density of X₁ conditioned on W₁ > 0 is therefore,

$\displaystyle p_{X_1}(x\vert\; W_1 > 0)=\begin{cases} \frac43\varphi(x),&{\rm for\ }x > 0,\\ \frac43\varphi(2x),&{\rm for\ }x < 0. \end{cases}$

Conditioned on W₁ < 0, we have already shown that the density is 4φ(2x) over x < 0 so, taking the average of these, we obtain

$\displaystyle p_{X_1}(x)=\begin{cases} \frac23\varphi(x),&{\rm for\ }x > 0,\\ \frac83\varphi(2x),&{\rm for\ }x < 0. \end{cases}$

This is plotted in figure 3 below, agreeing with So’s numerical estimation from the Twitter post shown in figure 1 above.

Model-Independent Discrete Barrier Adjustments

I continue the investigation of discrete barrier approximations started in an earlier post. The idea is to find good approximations to a continuous barrier condition, while only sampling the process at a discrete set of times. The difference now is that I will look at model independent methods which do not explicitly depend on properties of the underlying process, such as the volatility. This will enable much more generic adjustments which can be applied more easily and more widely. I point out now, the techniques that I will describe here are original research and cannot currently be found in the literature outside of this blog, to the best of my knowledge.

Recall that the problem is to compute the expected value of a function of a stochastic process X,

$\displaystyle V={\mathbb E}\left[f(X_T);\;\sup{}_{t\le T}X_t \ge K\right]$

(1)

which depends on whether or not the process crosses a continuous barrier level K. In many applications, such as with Monte Carlo simulation, we typically only sample X at a discrete set of times 0 < t₁ < t₂ < ⋯< t_n = T. In that case, the continuous barrier is necessarily approximated by a discrete one

$\displaystyle V={\mathbb E}\left[f(X_T);\;\sup{}_{i=1,\ldots,n}X_{t_i}\ge K\right].$

(2)

As we saw, this converges slowly as the number n of sampling times increases, with the error between this and the limiting continuous barrier (1) only going to zero at rate 1/√n.

A barrier adjustment as described in the earlier post is able to improve this convergence rate. If X is a Brownian motion with constant drift μ and positive volatility σ, then the discrete barrier level K is shifted down by an amount βσ√δt where β ≈ 0.5826 is a constant and δt = T/n is the sampling width. We are assuming, for now, that the sampling times are equally spaced. As was seen, using the shifted barrier level in (2) improves the rate of convergence. Although we did not theoretically derive the new convergence rate, numerical experiment suggests that it is close to 1/n.

Another way to express this is to shift the values of X up,

$\displaystyle M_i=X_{t_i}+\beta\sigma\sqrt{\delta t}.$

(3)

Then, (2) is replaced to use these shifted values, which are a proxy for the maximum value of X across each of the intervals (t_i-1, t_i),

$\displaystyle V={\mathbb E}\left[f(X_T);\;\sup{}_{i=1,\ldots,n}M_i\ge K\right].$

(4)

As it is equivalent to shifting the level K down, we still obtain the improved rate of convergence.

This idea is especially useful because of its generality. For non-equally spaced sampling times, the adjustment (3) can still be applied. Now, we just set δt = t_i – t_i-1 to be the spacing for the specific time, so depends on index i. It can also be used for much more general expressions than (1). Any function of X which depends on whether or not it crosses a continuous barrier can potentially make use of the adjustment described. Even if X is an Ito process with time dependent drift and volatility

$\displaystyle dX_t=\sigma_t\,dB_t+\mu_t\,dt,$

(5)

the method can be applied. Now, the volatility in (3) is replaced by an average value across the interval (t_i-1, t_i).

The methods above are very useful, but there is a further improvement that can be made. Ideally, we would not have to specify an explicit value of the volatility σ. That is, it should be model independent. There are many reasons why this is desirable. Suppose that we are running a Monte Carlo simulation and generate samples of X at the times t_i. If the simulation only outputs values of X, then this is not sufficient to compute (3). So, it will be necessary to update the program running the simulation to also output the volatility. In some situations this might not be easy. For example, X could be a complicated function of various other processes and, although we could use Ito’s lemma to compute the volatility of X from the other processes, it could be messy. In some situations we might not even have access to the volatility or any method of computing it. For example, the values of X could be computed from historical data. We could be looking at the probability of stock prices crossing a level by looking at historical close fixings, without access to the complete intra-day data. In any case, a model independent discrete barrier adjustment would make applying it much easier.

Removing Volatility Dependence

How can the volatility term be removed from adjustment (3)? One idea is to replace it by an estimator computed from the samples of X, such as

$\displaystyle \hat\sigma^2=\frac1T\sum_{i=1}^n(X_{t_i}-X_{t_{i-1}})^2.$

While this would work, at least for a constant volatility process, it does not meet the requirements. For a general Ito process (5) with stochastic volatility, using an estimator computed over the whole time interval [0, T] may not be a good approximation for the volatility at the time that the barrier is hit. A possible way around this is for the adjustment (3) applied at time t_i to only depend on a volatility estimator computed from samples near the time. This would be possible, although it is not clear what is the best way to select these times. Besides, an important point to note is that we do not need a good estimate of the volatility, since that is not the goal here.

As explained in the previous post, adjustment (3) works because it corrects for the expected overshoot when the barrier is hit. Specifically, at the first time for which M_i ≥ K, the overshoot is R = X_t_i – K. If there was no adjustment then the overshoot is positive and the leading order term in the discrete barrier approximation error is proportional to 𝔼[R]. The positive shift added to X_t_i is chosen to compensate for this, giving zero expected overshoot to leading order, and reducing the barrier approximation error. The same applies to any similar adjustment. As long as there is sufficient freedom in choosing M_i, then it should be possible to do it in a way that has zero expected overshoot. Taking this to the extreme, it should be possible to compute the adjustment at time t_i using only the sampled values X_t_i-1 and X_t_i.

Consider adjustments of the form

$\displaystyle M_i=\theta(X_{t_{i-1}},X_{t_i})$

for θ: ℝ² → ℝ. By model independence, if this adjustment applies to a process X, then it should equally apply to the shifted and scaled processes X + a and bX for constants a and b > 0. Equivalently, θ satisfies the scaling and translation invariance,

$\displaystyle \begin{aligned} &\theta(x+a,y+a)=\theta(x,y)+a,\\ &\theta(bx,by)=b\theta(x,y). \end{aligned}$

(6)

This restricts the possible forms that θ can take.

Lemma 1 A function θ: ℝ² → ℝ satisfies (6) if and only if

$\displaystyle \theta(x,y)=py+(1-p)x+c\lvert y-x\rvert$

for constants p, c.

Proof: Write θ(0, u) as the sum of its antisymmetric and symmetric parts

$\displaystyle \theta(0,u)=(\theta(0,u)-\theta(0,-u))/2+(\theta(0,u)+\theta(0,-u))/2.$

By scaling invariance, the first term on the right is proportional to u and the second is proportional to |u|. Hence,

$\displaystyle \theta(0,u)=pu+c\lvert u\rvert$

for constants p and c. Using translation invariance,

$\displaystyle \begin{aligned} \theta(x,y) &= x + \theta(0,y-x)\\ &=x + p(y-x)+c\lvert y-x\rvert \end{aligned}$

as required. ⬜

I will therefore only consider adjustments where the maximum of the process across the interval (t_i-1, t_i) is replaced by

$\displaystyle M_i=pX_{t_i}+(1-p)X_{t_{i-1}}+c\lvert X_{t_i}-X_{t_{i-1}}\rvert.$

(7)

According to (3), the barrier condition sup_t≤TX_t ≥ K is replaced by the discrete approximation max_iM_i ≥ K.

There are various ways in which (7) can be parameterized, but this form is quite intuitive. The term pX_t_i + (1 - p)X_t_i-1 is an interpolation of the path of X, and c|X_t_i – X_t_i-1| represents a shift proportional to the sample deviation across the interval replacing the σ√δt term of the simple shift (3). The purpose of this post is to find values for p and c giving a good adjustment, improving convergence of the discrete approximation.

The discrete barrier condition M_i ≥ K given by (7) can be satisfied while the process is below the barrier level, giving a negative barrier ‘overshoot’ R = X_t_i – K as in figure 2. As we will see, this is vital to obtaining an accurate approximation for the hitting probability. Continue reading “Model-Independent Discrete Barrier Adjustments” →

Pathwise Burkholder-Davis-Gundy Inequalities

As covered earlier in my notes, the Burkholder-David-Gundy inequality relates the moments of the maximum of a local martingale M with its quadratic variation,

$\displaystyle c_p^{-1}{\mathbb E}[[M]^{p/2}_\tau]\le{\mathbb E}[\bar M_\tau^p]\le C_p{\mathbb E}[[M]^{p/2}_\tau].$

(1)

Here, ${\bar M_t\equiv\sup_{s\le t}\lvert M_s\rvert}$ is the running maximum, ${[M]}$ is the quadratic variation, ${\tau}$ is a stopping time, and the exponent ${p}$ is a real number greater than or equal to 1. Then, ${c_p}$ and ${C_p}$ are positive constants depending on p, but independent of the choice of local martingale and stopping time. Furthermore, for continuous local martingales, which are the focus of this post, the inequality holds for all ${p > 0}$ .

Since the quadratic variation used in my notes, by definition, starts at zero, the BDG inequality also required the local martingale to start at zero. This is not an important restriction, but it can be removed by requiring the quadratic variation to start at ${[M]_0=M_0^2}$ . Henceforth, I will assume that this is the case, which means that if we are working with the definition in my notes then we should add ${M_0^2}$ everywhere to the quadratic variation ${[M]}$ .

In keeping with the theme of the previous post on Doob’s inequalities, such martingale inequalities should have pathwise versions of the form

$\displaystyle c_p^{-1}[M]^{p/2}+\int\alpha dM\le\bar M^p\le C_p[M]^{p/2}+\int\beta dM$

(2)

for predictable processes ${\alpha,\beta}$ . Inequalities in this form are considerably stronger than (1), since they apply on all sample paths, not just on average. Also, we do not require M to be a local martingale — it is sufficient to be a (continuous) semimartingale. However, in the case where M is a local martingale, the pathwise version (2) does imply the BDG inequality (1), using the fact that stochastic integration preserves the local martingale property.

Lemma 1 Let X and Y be nonnegative increasing measurable processes satisfying ${X\le Y-N}$ for a local (sub)martingale N starting from zero. Then, ${{\mathbb E}[X_\tau]\le{\mathbb E}[Y_\tau]}$ for all stopping times ${\tau}$ .

Proof: Let ${\tau_n}$ be an increasing sequence of bounded stopping times increasing to infinity such that the stopped processes ${N^{\tau_n}}$ are submartingales. Then,

$\displaystyle {\mathbb E}[1_{\{\tau_n\ge\tau\}}X_\tau]\le{\mathbb E}[X_{\tau_n\wedge\tau}]={\mathbb E}[Y_{\tau_n\wedge\tau}]-{\mathbb E}[N_{\tau_n\wedge\tau}]\le{\mathbb E}[Y_{\tau_n\wedge\tau}]\le{\mathbb E}[Y_\tau].$

Letting n increase to infinity and using monotone convergence on the left hand side gives the result. ⬜

Moving on to the main statements of this post, I will mention that there are actually many different pathwise versions of the BDG inequalities. I opt for the especially simple statements given in Theorem 2 below. See the papers Pathwise Versions of the Burkholder-Davis Gundy Inequality by Bieglböck and Siorpaes, and Applications of Pathwise Burkholder-Davis-Gundy inequalities by Soirpaes, for slightly different approaches, although these papers do also effectively contain proofs of (3,4) for the special case of ${r=1/2}$ . As usual, I am using ${x\vee y}$ to represent the maximum of two numbers.

Theorem 2 Let X and Y be nonnegative continuous processes with ${X_0=Y_0}$ . For any ${0 < r\le1}$ we have,

$\displaystyle (1-r)\bar X^r\le (3-2r)\bar Y^r+r\int(\bar X\vee\bar Y)^{r-1}d(X-Y)$ (3)

and, if X is increasing, this can be improved to,

$\displaystyle \bar X^r\le (2-r)\bar Y^r+r\int(\bar X\vee\bar Y)^{r-1}d(X-Y).$ (4)

If ${r\ge1}$ and X is increasing then,

$\displaystyle \bar X^r\le r^{r\vee 2}\,\bar Y^r+r^2\int(\bar X\vee\bar Y)^{r-1}d(X-Y).$ (5)

Continue reading “Pathwise Burkholder-Davis-Gundy Inequalities” →

Pathwise Martingale Inequalities

Recall Doob’s inequalities, covered earlier in these notes, which bound expectations of functions of the maximum of a martingale in terms of its terminal distribution. Although these are often applied to martingales, they hold true more generally for cadlag submartingales. Here, I use ${\bar X_t\equiv\sup_{s\le t}X_s}$ to denote the running maximum of a process.

Theorem 1 Let X be a nonnegative cadlag submartingale. Then,

${{\mathbb P}\left(\bar X_t \ge K\right)\le K^{-1}{\mathbb E}[X_t]}$ for all ${K > 0}$ .

${\lVert\bar X_t\rVert_p\le (p/(p-1))\lVert X_t\rVert_p}$ for all ${p > 1}$ .

${{\mathbb E}[\bar X_t]\le(e/(e-1)){\mathbb E}[X_t\log X_t+1]}$ .

In particular, for a cadlag martingale X, then ${\lvert X\rvert}$ is a submartingale, so theorem 1 applies with ${\lvert X\rvert}$ in place of X.

We also saw the following much stronger (sub)martingale inequality in the post on the maximum maximum of martingales with known terminal distribution.

Theorem 2 Let X be a cadlag submartingale. Then, for any real K and nonnegative real t,

$\displaystyle {\mathbb P}(\bar X_t\ge K)\le\inf_{x < K}\frac{{\mathbb E}[(X_t-x)_+]}{K-x}.$ (1)

This is particularly sharp, in the sense that for any distribution for ${X_t}$ , there exists a martingale with this terminal distribution for which (1) becomes an equality simultaneously for all values of K. Furthermore, all of the inequalities stated in theorem 1 follow from (1). For example, the first one is obtained by taking ${x=0}$ in (1). The remaining two can also be proved from (1) by integrating over K.

Note that all of the submartingale inequalities above are of the form

$\displaystyle {\mathbb E}[F(\bar X_t)]\le{\mathbb E}[G(X_t)]$

(2)

for certain choices of functions ${F,G\colon{\mathbb R}\rightarrow{\mathbb R}^+}$ . The aim of this post is to show how they have a more general `pathwise’ form,

$\displaystyle F(\bar X_t)\le G(X_t) - \int_0^t\xi\,dX$

(3)

for some nonnegative predictable process ${\xi}$ . It is relatively straightforward to show that (2) follows from (3) by noting that the integral is a submartingale and, hence, has nonnegative expectation. To be rigorous, there are some integrability considerations to deal with, so a proof will be included later in this post.

Inequality (3) is required to hold almost everywhere, and not just in expectation, so is a considerably stronger statement than the standard martingale inequalities. Furthermore, it is not necessary for X to be a submartingale for (3) to make sense, as it holds for all semimartingales. We can go further, and even drop the requirement that X is a semimartingale. As we will see, in the examples covered in this post, ${\xi_t}$ will be of the form ${h(\bar X_{t-})}$ for an increasing right-continuous function ${h\colon{\mathbb R}\rightarrow{\mathbb R}}$ , so integration by parts can be used,

$\displaystyle \int h(\bar X_-)\,dX = h(\bar X)X-h(\bar X_0)X_0 - \int X\,dh(\bar X).$

(4)

The right hand side of (4) is well-defined for any cadlag real-valued process, by using the pathwise Lebesgue–Stieltjes integral with respect to the increasing process ${h(\bar X)}$ , so can be used as the definition of ${\int h(\bar X_-)dX}$ . In the case where X is a semimartingale, integration by parts ensures that this agrees with the stochastic integral ${\int\xi\,dX}$ . Since we now have an interpretation of (3) in a pathwise sense for all cadlag processes X, it is no longer required to suppose that X is a submartingale, a semimartingale, or even require the existence of an underlying probability space. All that is necessary is for ${t\mapsto X_t}$ to be a cadlag real-valued function. Hence, we reduce the martingale inequalities to straightforward results of real-analysis not requiring any probability theory and, consequently, are much more general. I state the precise pathwise generalizations of Doob’s inequalities now, leaving the proof until later in the post. As the first of inequality of theorem 1 is just the special case of (1) with ${x=0}$ , we do not need to explicitly include this here.

Theorem 3 Let X be a cadlag process and t be a nonnegative time.

For real ${K > x}$ ,

$\displaystyle 1_{\{\bar X_t\ge K\}}\le\frac{(X_t-x)_+}{K-x}-\int_0^t\xi\,dX$ (5)

where ${\xi=(K-x)^{-1}1_{\{\bar X_-\ge K\}}}$ .

If X is nonnegative and p,q are positive reals with ${p^{-1}+q^{-1}=1}$ then,

$\displaystyle \bar X_t^p\le q^p X^p_t-\int_0^t\xi dX$ (6)

where ${\xi=pq\bar X_-^{p-1}}$ .

If X is nonnegative then,

$\displaystyle \bar X_t\le\frac{e}{e-1}\left( X_t \log X_t +1\right)-\int_0^t\xi\,dX$ (7)

where ${\xi=\frac{e}{e-1}\log(\bar X_-\vee1)}$ .

Continue reading “Pathwise Martingale Inequalities” →

Proof of Measurable Section

I will give a proof of the measurable section theorem, also known as measurable selection. Given a complete probability space ${(\Omega,\mathcal F,{\mathbb P})}$ , we denote the projection from ${\Omega\times{\mathbb R}}$ by

$\displaystyle \setlength\arraycolsep{2pt} \begin{array}{rl} &\displaystyle\pi_\Omega\colon \Omega\times{\mathbb R}\rightarrow\Omega,\smallskip\\ &\displaystyle\pi_\Omega(\omega,t)=\omega. \end{array}$

By definition, if ${S\subseteq\Omega\times{\mathbb R}}$ then, for every ${\omega\in\pi_\Omega(S)}$ , there exists a ${t\in{\mathbb R}}$ such that ${(\omega,t)\in S}$ . The measurable section theorem says that this choice can be made in a measurable way. That is, using ${\mathcal B({\mathbb R})}$ to denote the Borel sigma-algebra, if S is in the product sigma-algebra ${\mathcal F\otimes\mathcal B({\mathbb R})}$ then ${\pi_\Omega(S)\in\mathcal F}$ and there is a measurable map

$\displaystyle \setlength\arraycolsep{2pt} \begin{array}{rl} &\displaystyle\tau\colon\pi_\Omega(S)\rightarrow{\mathbb R},\smallskip\\ &\displaystyle(\omega,\tau(\omega))\in S. \end{array}$

It is convenient to extend ${\tau}$ to the whole of ${\Omega}$ by setting ${\tau=\infty}$ outside of ${\pi_\Omega(S)}$ .

measurable section — Figure 1: A section of a measurable set

We consider measurable functions ${\tau\colon\Omega\rightarrow{\mathbb R}\cup\{\infty\}}$ . The graph of ${\tau}$ is

$\displaystyle [\tau]=\left\{(\omega,\tau(\omega))\colon\tau(\omega)\in{\mathbb R}\right\}\subseteq\Omega\times{\mathbb R}.$

The condition that ${(\omega,\tau(\omega))\in S}$ whenever ${\tau < \infty}$ can then be expressed by stating that ${[\tau]\subseteq S}$ . This also ensures that ${\{\tau < \infty\}}$ is a subset of ${\pi_\Omega(S)}$ , and ${\tau}$ is a section of S on the whole of ${\pi_\Omega(S)}$ if and only if ${\{\tau < \infty\}=\pi_\Omega(S)}$ .

The proof of the measurable section theorem will make use of the properties of analytic sets and of the Choquet capacitability theorem, as described in the previous two posts. [Note: I have since posted a more direct proof which does not involve such prerequisites.] Recall that a paving ${\mathcal E}$ on a set X denotes, simply, a collection of subsets of X. The pair ${(X,\mathcal E)}$ is then referred to as a paved space. Given a pair of paved spaces ${(X,\mathcal E)}$ and ${(Y,\mathcal F)}$ , the product paving ${\mathcal E\times\mathcal F}$ denotes the collection of cartesian products ${A\times B}$ for ${A\in\mathcal E}$ and ${B\in\mathcal F}$ , which is a paving on ${X\times Y}$ . The notation ${\mathcal E_\delta}$ is used for the collection of countable intersections of a paving ${\mathcal E}$ .

We start by showing that measurable section holds in a very simple case where, for the section of a set S, its debut will suffice. The debut is the map

$\displaystyle \setlength\arraycolsep{2pt} \begin{array}{rl} &\displaystyle D(S)\colon\Omega\rightarrow{\mathbb R}\cup\{\pm\infty\},\smallskip\\ &\displaystyle \omega\mapsto\inf\left\{t\in{\mathbb R}\colon (\omega,t)\in S\right\}. \end{array}$

We use the convention that the infimum of the empty set is ${\infty}$ . It is not clear that ${D(S)}$ is measurable, and we do not rely on this, although measurable projection can be used to show that it is measurable whenever S is in ${\mathcal F\otimes\mathcal B({\mathbb R})}$ .

Lemma 1 Let ${(\Omega,\mathcal F)}$ be a measurable space, ${\mathcal K}$ be the collection of compact intervals in ${{\mathbb R}}$ , and ${\mathcal E}$ be the closure of the paving ${\mathcal{F\times K}}$ under finite unions.

Then, the debut ${D(S)}$ of any ${S\in\mathcal E_\delta}$ is measurable and its graph ${[D(S)]}$ is contained in S.

Continue reading “Proof of Measurable Section” →

Choquet’s Capacitability Theorem and Measurable Projection

In this post I will give a proof of the measurable projection theorem. Recall that this states that for a complete probability space ${(\Omega,\mathcal F,{\mathbb P})}$ and a set S in the product sigma-algebra ${\mathcal F\otimes\mathcal B({\mathbb R})}$ , the projection, ${\pi_\Omega(S)}$ , of S onto ${\Omega}$ , is in ${\mathcal F}$ . The previous post on analytic sets made some progress towards this result. Indeed, using the definitions and results given there, it follows quickly that ${\pi_\Omega(S)}$ is ${\mathcal F}$ -analytic. To complete the proof of measurable projection, it is necessary to show that analytic sets are measurable. This is a consequence of Choquet’s capacitability theorem, which I will prove in this post. Measurable projection follows as a simple consequence.

The condition that the underlying probability space is complete is necessary and, if this condition was dropped, then the result would no longer hold. Recall that, if ${(\Omega,\mathcal F,{\mathbb P})}$ is a probability space, then the completion, ${\mathcal F_{\mathbb P}}$ , of ${\mathcal F}$ with respect to ${{\mathbb P}}$ consists of the sets ${A\subseteq\Omega}$ such that there exists ${B,C\in\mathcal F}$ with ${B\subseteq A\subseteq C}$ and ${{\mathbb P}(B)={\mathbb P}(C)}$ . The probability space is complete if ${\mathcal F_{\mathbb P}=\mathcal F}$ . More generally, ${{\mathbb P}}$ can be uniquely extended to a measure ${\bar{\mathbb P}}$ on the sigma-algebra ${\mathcal F_{\mathbb P}}$ by setting ${\bar{\mathbb P}(A)={\mathbb P}(B)={\mathbb P}(C)}$ , where B and C are as above. Then ${(\Omega,\mathcal F_{\mathbb P},\bar{\mathbb P})}$ is the completion of ${(\Omega,\mathcal F,{\mathbb P})}$ .

In measurable projection, then, it needs to be shown that if ${A\subseteq\Omega}$ is the projection of a set in ${\mathcal F\otimes\mathcal B({\mathbb R})}$ , then A is in the completion of ${\mathcal F}$ . That is, we need to find sets ${B,C\in\mathcal F}$ with ${B\subseteq A\subseteq C}$ with ${{\mathbb P}(B)={\mathbb P}(C)}$ . In fact, it is always possible to find a ${C\supseteq A}$ in ${\mathcal F}$ which minimises ${{\mathbb P}(C)}$ , and its measure is referred to as the outer measure of A. For any probability measure ${{\mathbb P}}$ , we can define an outer measure on the subsets of ${\Omega}$ , ${{\mathbb P}^*\colon\mathcal P(\Omega)\rightarrow{\mathbb R}^+}$ by approximating ${A\subseteq\Omega}$ from above,

$\displaystyle {\mathbb P}^*(A)\equiv\inf\left\{{\mathbb P}(B)\colon B\in\mathcal F, A\subseteq B\right\}.$

(1)

Similarly, we can define an inner measure by approximating A from below,

$\displaystyle {\mathbb P}_*(A)\equiv\sup\left\{{\mathbb P}(B)\colon B\in\mathcal F, B\subseteq A\right\}.$

It can be shown that A is ${\mathcal F}$ -measurable if and only if ${{\mathbb P}_*(A)={\mathbb P}^*(A)}$ . We will be concerned primarily with the outer measure ${{\mathbb P}^*}$ , and will show that that if A is the projection of some ${S\in\mathcal F\otimes\mathcal B({\mathbb R})}$ , then A can be approximated from below in the following sense: there exists ${B\subseteq A}$ in ${\mathcal F}$ for which ${{\mathbb P}^*(B)={\mathbb P}^*(A)}$ . From this, it will follow that A is in the completion of ${\mathcal F}$ .

It is convenient to prove the capacitability theorem in slightly greater generality than just for the outer measure ${{\mathbb P}^*}$ . The only properties of ${{\mathbb P}^*}$ that are required is that it is a capacity, which we now define. Recall that a paving ${\mathcal E}$ on a set X is simply any collection of subsets of X, and we refer to the pair ${(X,\mathcal E)}$ as a paved space.

Definition 1 Let ${(X,\mathcal E)}$ be a paved space. Then, an ${\mathcal E}$ -capacity is a map ${I\colon\mathcal P(X)\rightarrow{\mathbb R}}$ which is increasing, continuous along increasing sequences, and continuous along decreasing sequences in ${\mathcal E}$ . That is,

if ${A\subseteq B}$ then ${I(A)\le I(B)}$ .

if ${A_n\subseteq X}$ is increasing in n then ${I(A_n)\rightarrow I(\bigcup_nA_n)}$ as ${n\rightarrow\infty}$ .

if ${A_n\in\mathcal E}$ is decreasing in n then ${I(A_n)\rightarrow I(\bigcap_nA_n)}$ as ${n\rightarrow\infty}$ .

As was claimed above, the outer measure ${{\mathbb P}^*}$ defined by (1) is indeed a capacity.

Lemma 2 Let ${(\Omega,\mathcal F,{\mathbb P})}$ be a probability space. Then,

${{\mathbb P}^*(A)={\mathbb P}(A)}$ for all ${A\in\mathcal F}$ .

For all ${A\subseteq\Omega}$ , there exists a ${B\in\mathcal F}$ with ${A\subseteq B}$ and ${{\mathbb P}^*(A)={\mathbb P}(B)}$ .

${{\mathbb P}^*}$ is an ${\mathcal F}$ -capacity.

Continue reading “Choquet’s Capacitability Theorem and Measurable Projection” →

Analytic Sets

We will shortly give a proof of measurable projection and, also, of the section theorems. Starting with the projection theorem, recall that this states that if ${(\Omega,\mathcal F,{\mathbb P})}$ is a complete probability space, then the projection of any measurable subset of ${\Omega\times{\mathbb R}}$ onto ${\Omega}$ is measurable. To be precise, the condition is that S is in the product sigma-algebra ${\mathcal{F}\otimes\mathcal B({\mathbb R})}$ , where ${\mathcal B({\mathbb R})}$ denotes the Borel sets in ${{\mathbb R}}$ , and ${\pi\colon\Omega\times{\mathbb R}\rightarrow\Omega}$ is the projection ${\pi(\omega,t)=\omega}$ . Then, ${\pi(S)\in\mathcal{F}}$ . Although it looks like a very basic property of measurable sets, maybe even obvious, measurable projection is a surprisingly difficult result to prove. In fact, the requirement that the probability space is complete is necessary and, if it is dropped, then ${\pi(S)}$ need not be measurable. Counterexamples exist for commonly used measurable spaces such as ${\Omega= {\mathbb R}}$ and ${\mathcal F=\mathcal B({\mathbb R})}$ . This suggests that there is something deeper going on here than basic manipulations of measurable sets.

The techniques which will be used to prove the projection theorem involve analytic sets, which will be introduced in this post, with the proof of measurable projection to follow in the next post. [Note: I have since posted a more direct proof of measurable projection and section, which does not make use of analytic sets.] These results can also be used to prove the optional and predictable section theorems which, at first appearances, seem to be quite basic statements. The section theorems are fundamental to the powerful and interesting theory of optional and predictable projection which is, consequently, generally considered to be a hard part of stochastic calculus. In fact, the projection and section theorems are really not that hard to prove, although the method given here does require stepping outside of the usual setup used in probability and involves something more like descriptive set theory. Continue reading “Analytic Sets” →

Do Convex and Decreasing Functions Preserve the Semimartingale Property?

Some years ago, I spent considerable effort trying to prove the hypothesis below. After failing at this, I spent time trying to find a counterexample, but also with no success. I did post this as a question on mathoverflow, but it has so far received no conclusive answers. So, as far as I am aware, the following statement remains unproven either way.

Hypothesis H1 Let ${f\colon{\mathbb R}_+\times{\mathbb R}\rightarrow{\mathbb R}}$ be such that ${f(t,x)}$ is convex in x and right-continuous and decreasing in t. Then, for any semimartingale X, ${f(t,X_t)}$ is a semimartingale.

It is well known that convex functions of semimartingales are themselves semimartingales. See, for example, the Ito-Tanaka formula. More generally, if ${f(t,x)}$ was increasing in t rather than decreasing, then it can be shown without much difficulty that ${f(t,X_t)}$ is a semimartingale. Consider decomposing ${f(t,X_t)}$ as

$\displaystyle f(t,X_t)=\int_0^tf_x(s,X_{s-})\,dX_s+V_t,$

(1)

for some process V. By convexity, the right hand derivative of ${f(t,x)}$ with respect to x always exists, and I am denoting this by ${f_x}$ . In the case where f is twice continuously differentiable then the process V is given by Ito’s formula which, in particular, shows that it is a finite variation process. If ${f(t,x)}$ is convex in x and increasing in t, then the terms in Ito’s formula for V are all increasing and, so, it is an increasing process. By taking limits of smooth functions, it follows that V is increasing even when the differentiability constraints are dropped, so ${f(t,X_t)}$ is a semimartingale. Now, returning to the case where ${f(t,x)}$ is decreasing in t, Ito’s formula is only able to say that V is of finite variation, and is generally not monotonic. As limits of finite variation processes need not be of finite variation themselves, this does not say anything about the case when f is not assumed to be differentiable, and does not help us to determine whether or not ${f(t,X_t)}$ is a semimartingale.

Hypothesis H1 can be weakened by restricting to continuous functions of continuous martingales.

Hypothesis H2 Let ${f\colon{\mathbb R}_+\times{\mathbb R}\rightarrow{\mathbb R}}$ be such that ${f(t,x)}$ is convex in x and continuous and decreasing in t. Then, for any continuous martingale X, ${f(t,X_t)}$ is a semimartingale.

As continuous martingales are special cases of semimartingales, hypothesis H1 implies H2. In fact, the reverse implication also holds so that hypotheses H1 and H2 are equivalent.

Hypotheses H1 and H2 can also be recast as a simple real analysis statement which makes no reference to stochastic processes.

Hypothesis H3 Let ${f\colon{\mathbb R}_+\times{\mathbb R}\rightarrow{\mathbb R}}$ be such that ${f(t,x)}$ is convex in x and decreasing in t. Then, ${f=g-h}$ where ${g(t,x)}$ and ${h(t,x)}$ are convex in x and increasing in t.

Continue reading “Do Convex and Decreasing Functions Preserve the Semimartingale Property?” →

Failure of the Martingale Property For Stochastic Integration

If X is a cadlag martingale and ${\xi}$ is a uniformly bounded predictable process, then is the integral

$\displaystyle Y=\int\xi\,dX$

(1)

a martingale? If ${\xi}$ is elementary this is one of most basic properties of martingales. If X is a square integrable martingale, then so is Y. More generally, if X is an ${L^p}$ -integrable martingale, any ${p > 1}$ , then so is Y. Furthermore, integrability of the maximum ${\sup_{s\le t}\lvert X_s\rvert}$ is enough to guarantee that Y is a martingale. Also, it is a fundamental result of stochastic integration that Y is at least a local martingale and, for this to be true, it is only necessary for X to be a local martingale and ${\xi}$ to be locally bounded. In the general situation for cadlag martingales X and bounded predictable ${\xi}$ , it need not be the case that Y is a martingale. In this post I will construct an example showing that Y can fail to be a martingale. Continue reading “Failure of the Martingale Property For Stochastic Integration” →

The Optimality of Doob’s Maximal Inequality

One of the most fundamental and useful results in the theory of martingales is Doob’s maximal inequality. Use ${X^*_t\equiv\sup_{s\le t}\lvert X_s\rvert}$ to denote the running (absolute) maximum of a process X. Then, Doob’s ${L^p}$ maximal inequality states that, for any cadlag martingale or nonnegative submartingale X and real ${p > 1}$ ,

$\displaystyle \lVert X^*_t\rVert_p\le c_p \lVert X_t\rVert_p$

(1)

with ${c_p=p/(p-1)}$ . Here, ${\lVert\cdot\rVert_p}$ denotes the standard L^p-norm, ${\lVert U\rVert_p\equiv{\mathbb E}[U^p]^{1/p}}$ .

An obvious question to ask is whether it is possible to do any better. That is, can the constant ${c_p}$ in (1) be replaced by a smaller number. This is especially pertinent in the case of small p, since ${c_p}$ diverges to infinity as p approaches 1. The purpose of this post is to show, by means of an example, that the answer is no. The constant ${c_p}$ in Doob’s inequality is optimal. We will construct an example as follows.

Example 1 For any ${p > 1}$ and constant ${1 \le c < c_p}$ there exists a strictly positive cadlag ${L^p}$ -integrable martingale ${\{X_t\}_{t\in[0,1]}}$ with ${X^*_1=cX_1}$ .

For X as in the example, we have ${\lVert X^*_1\rVert_p=c\lVert X_1\rVert_p}$ . So, supposing that (1) holds with any other constant ${\tilde c_p}$ in place of ${c_p}$ , we must have ${\tilde c_p\ge c}$ . By choosing ${c}$ as close to ${c_p}$ as we like, this means that ${\tilde c_p\ge c_p}$ and ${c_p}$ is indeed optimal in (1). Continue reading “The Optimality of Doob’s Maximal Inequality” →

	Anonymous on Spitzer’s Formula
	Anonymous on Spitzer’s Formula
	Anonymous on Brownian Bridges
	Anonymous on Spitzer’s Formula
	Anonymous on Spitzer’s Formula
	Anonymous on Spitzer’s Formula
	Anonymous on Spitzer’s Formula
	Anonymous on Spitzer’s Formula
	Anonymous on Spitzer’s Formula
	Anonymous on Spitzer’s Formula